代码随想录算法训练营第十四天|二叉树的递归遍历、二叉树的迭代遍历
二叉树的理论基础
参考资料(代码随想录)
二叉树的递归遍历
参考资料(代码随想录)
思路
递归算法的三个要素:
-
确定递归函数的参数和返回值: 确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数, 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
-
确定终止条件: 写完了递归算法, 运行的时候,经常会遇到栈溢出的错误,就是没写终止条件或者终止条件写的不对,操作系统也是用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然就会溢出。
-
确定单层递归的逻辑: 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。
代码如下(JavaScript)
前序遍历:
中序遍历:
后序遍历:
案例
144.二叉树的前序遍历
题目
力扣题目链接
代码如下(JavaScript)
var preorderTraversal = function(root) {
let res=[]
const dfs=function(root){
if(root==null) return
//先序遍历所以从父节点开始
res.push(root.val)
//递归左子树
dfs(root.left)
//递归右子树
dfs(root.right)
}
dfs(root)
return res
};94.二叉树的中序遍历
题目
力扣题目链接
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
代码如下(JavaScript)
var inorderTraversal = function(root) {
const res=[]
const dfs= function(root){
if(root===null){
return
}
dfs(root.left)
res.push(root.val)
dfs(root.right)
}
dfs(root)
return res
};145.二叉树的后序遍历
题目
力扣题目链接
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历
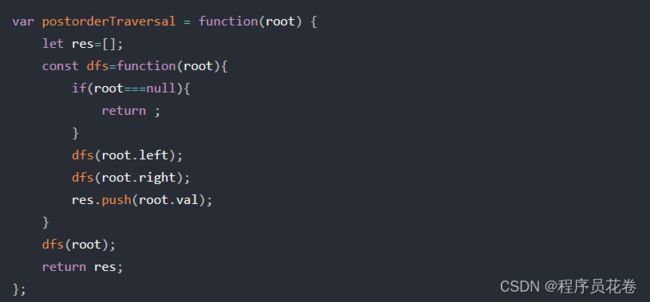
代码如下(JavaScript)
var postorderTraversal = function(root) {
const res=[]
const dfs= function(root){
if(root===null) return
dfs(root.left)
dfs(root.right)
res.push(root.val)
}
dfs(root)
return res
};二叉树的迭代遍历
参考资料(代码随想录)
思路
跟递归一样,我们也可以用栈来实现二叉树的前后中序遍历。
前序遍历(迭代法)
我们先看一下前序遍历。
前序遍历是中左右,每次先处理的是中间节点,那么先将根节点放入栈中,然后将右孩子加入栈,再加入左孩子。
为什么要先加入 右孩子,再加入左孩子呢? 因为这样出栈的时候才是中左右的顺序。
动画如下:
代码如下(JavaScript)
// 入栈 右 -> 左
// 出栈 中 -> 左 -> 右
var preorderTraversal = function(root, res = []) {
if(!root) return res;
const stack = [root];
let cur = null;
while(stack.length) {
cur = stack.pop();
res.push(cur.val);
cur.right && stack.push(cur.right);
cur.left && stack.push(cur.left);
}
return res;
};中序遍历(迭代法)
刚刚在迭代的过程中,我们有两个操作:
- 处理:将元素放进result数组中
- 访问:遍历节点
注意刚刚写的前序遍历的代码,不能和中序遍历通用,因为前序遍历的顺序是中左右,先访问的元素是中间节点,要处理的元素也是中间节点,所以刚刚才能写出相对简洁的代码,因为要访问的元素和要处理的元素顺序是一致的,都是中间节点。
那么再看看中序遍历,中序遍历是左中右,先访问的是二叉树顶部的节点,然后一层一层向下访问,直到到达树左面的最底部,再开始处理节点(也就是在把节点的数值放进result数组中),这就造成了处理顺序和访问顺序是不一致的。
那么在使用迭代法写中序遍历,就需要借用指针的遍历来帮助访问节点,栈则用来处理节点上的元素。
动画如下:
代码如下(JavaScript)
// 入栈 左 -> 右
// 出栈 左 -> 中 -> 右
var inorderTraversal = function(root, res = []) {
const stack = [];
let cur = root;
while(stack.length || cur) {
if(cur) {
stack.push(cur);
// 左
cur = cur.left;
} else {
// --> 弹出 中
cur = stack.pop();
res.push(cur.val);
// 右
cur = cur.right;
}
};
return res;
};后序遍历(迭代法)
再来看后序遍历,先序遍历是中左右,后续遍历是左右中,那么我们只需要调整一下先序遍历的代码顺序,就变成中右左的遍历顺序,然后在反转result数组,输出的结果顺序就是左右中了,如下图:
代码如下(JavaScript)
// 入栈 左 -> 右
// 出栈 左 -> 中 -> 右
var inorderTraversal = function(root, res = []) {
const stack = [];
let cur = root;
while(stack.length || cur) {
if(cur) {
stack.push(cur);
// 左
cur = cur.left;
} else {
// --> 弹出 中
cur = stack.pop();
res.push(cur.val);
// 右
cur = cur.right;
}
};
return res;
};总结
我们用迭代法写出了二叉树的前后中序遍历,大家可以看出前序和中序是完全两种代码风格,并不像递归写法那样代码稍做调整,就可以实现前后中序。
这是因为前序遍历中访问节点(遍历节点)和处理节点(将元素放进result数组中)可以同步处理,但是中序就无法做到同步!
案例
144.二叉树的前序遍历
题目
力扣题目链接
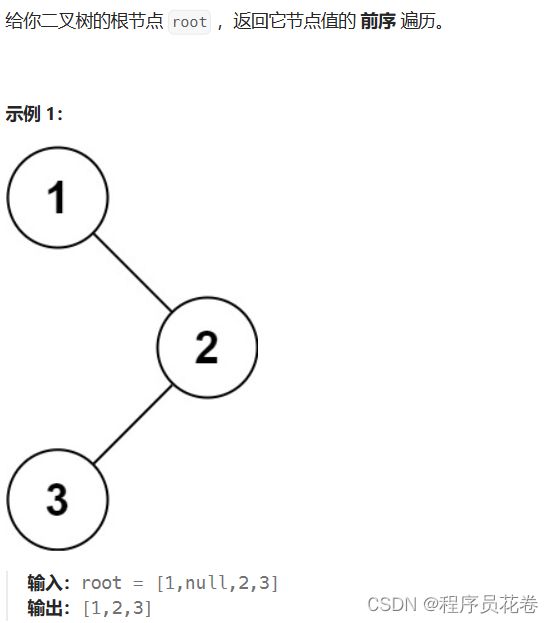
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
代码如下(JavaScript)
// 入栈 右 -> 左
// 出栈 中 -> 左 -> 右
var preorderTraversal = function(root ,res=[]) {
if(!root) return res
const stack=[root]
let cur=null
while(stack.length){
cur=stack.pop()
res.push(cur.val)
cur.right && stack.push(cur.right)
cur.left && stack.push(cur.left)
}
return res
};94.二叉树的中序遍历
题目
力扣题目链接
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
代码如下(JavaScript)
// 入栈 左 -> 右
// 出栈 左 -> 中 -> 右
var inorderTraversal = function(root,res=[]) {
const stack=[]
let cur =root
while(stack.length||cur){
if(cur){ //指针来访问节点,访问到最低层
stack.push(cur) //将访问的节点放进栈
//左
cur=cur.left
}else{
//弹出--- 中
cur=stack.pop() //从栈里弹出的数据,就是要处理的数据(放入res数组里的数据)
res.push(cur.val)
//右
cur=cur.right
}
}
return res
};145.二叉树的后序遍历
题目
力扣题目链接
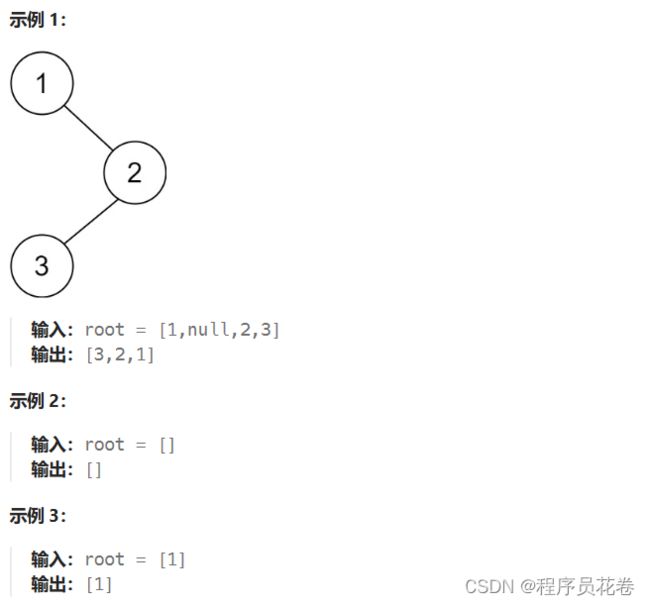
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
代码如下(JavaScript)
// 入栈 左 -> 右
// 出栈 中 -> 右 -> 左 结果翻转
var postorderTraversal = function(root,res=[]) {
if(!root) return res
const stack=[root]
let cur=null
while(stack.length){
cur=stack.pop()
res.push(cur.val)
cur.left && stack.push(cur.left)
cur.right && stack.push(cur.right)
}
return res.reverse()
};