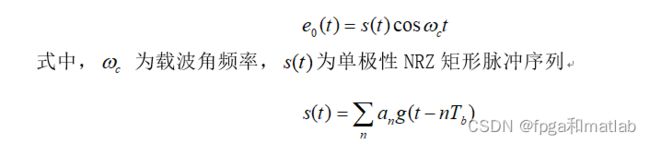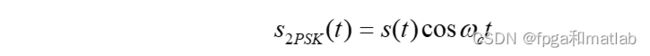数字调制方法实现的理论分析
目录
1.ASK
2.FSK
3.PSK
最常用实现数字调制方法是键控法:可获得振幅键控(Amplitude Shift Keying,ASK)、频移键控(Freqency Shift Keying,FSK)和相移键控(Phase Shift Keying, PSK).数字信息有二进制和多进制之分。
1.ASK
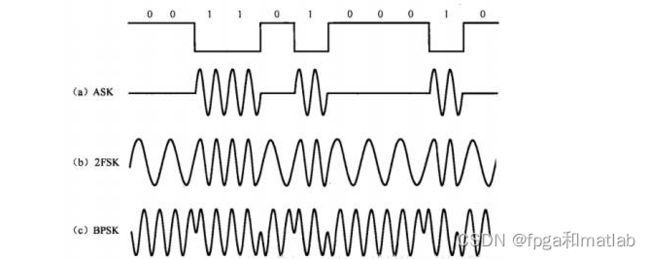
ASK调制,又称振幅键控,是一种数字调制技术,其中正弦载波的振幅随数字基带信号的变化而变化。在二进制ASK(2ASK)中,数字信息以二进制的形式(0或1)进行传输。当发送数字“1”时,载波信号存在并具有特定振幅;当发送数字“0”时,载波信号被抑制或降低到非常低的振幅。
数字幅度调制又称幅度键控(ASK),二进制幅度键控记作2ASK。2ASK是利用代表数字信息“0”或“1”的基带矩形脉冲去键控一个连续的载波,使载波时断时续地输出。有载波输出时表示发送“1”,无载波输出时表示发送“0”。根据幅度调制的原理,2ASK信号可表示为:
MATLAB简要程序如下:
m1=[];
c1=[];
for n=1:length(s)
if s(n)==0;
m=zeros(1,100);
else s(n)==1;
m=ones(1,100);
end
c=sin(f*t);
m1=[m1 m];
c1=[c1 c]
end
ask=c1.*m1;
subplot(211);
plot(m1)
title('原始信号');
axis([0 100*length(s) -0.1 1.1]);
subplot(212);
plot(ask)
title('ASK信号');
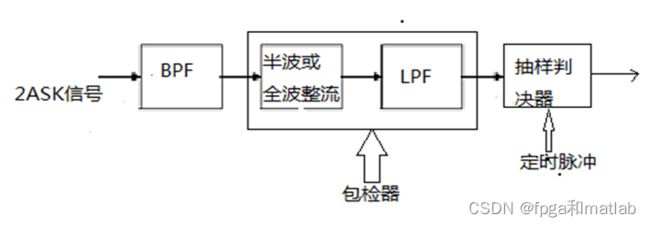
2ASK信号解调的常用方法主要有两种:包络检波法和相干检测法。其结构分别如下图所示:
ASK解调是从已调制的ASK信号中恢复原始数字基带信号的过程。解调可以分为非相干解调和相干解调两种方式。
- 非相干解调(包络检波法):
非相干解调是通过检测已调信号的包络来恢复基带信号。对于ASK信号,包络检波器可以检测信号的振幅变化,并将其转换为数字输出。当检测到高振幅时输出“1”,检测到低振幅或没有信号时输出“0”。 - 相干解调(同步检测法):
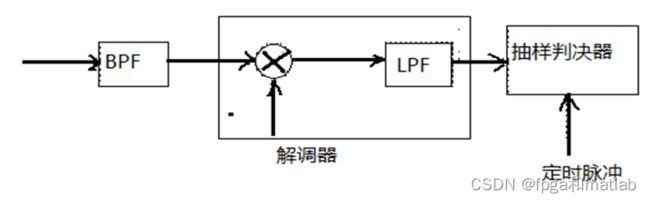
相干解调需要使用与载波同频同相的参考信号。通过将接收到的ASK信号与参考信号相乘,可以提取出基带信号。这种方法要求严格的同步,以确保参考信号与接收到的ASK信号相位一致。相干解调在性能上优于非相干解调,但实现起来更为复杂。
在实际应用中,根据通信系统的要求和条件选择合适的解调方法。ASK调制解调技术广泛应用于无线通信、遥控、遥测以及数字广播等领域。
ASK调制相对简单,容易实现,但其主要缺点是对于噪声和干扰较为敏感,特别是在信噪比低的情况下。因此,ASK通常用于低速率或短距离通信,如遥控器和无线门铃等。
2.FSK
数字频率调制又称频移键控(FSK),二进制频移键控记作2FSK。数字频移键控是用载波的频率来传送数字消息,即用所传送的数字消息控制载波的频率。2FSK信号便是符号“1”对应于载频,而符号“0”对应于载频f1与f2的已调波形,而且f1与f2之间的改变是瞬间完成的。
2FSK信号的数字表达式可以表示为:
MATLAB简要程序如下:
t=0:2*pi/99:2*pi;
m1=[];
c1=[];
b1=[];
for n=1:length(s)
if s(n)==0;
m=ones(1,100);
c=sin(f2*t);
b=zeros(1,100)
else s(n)==1;
m=ones(1,100);
c=sin(f1*t);
b=ones(1,100)
end
m1=[m1 m];
c1=[c1 c];
b1=[b1 b];
end
fsk=c1.*m1;
subplot(211);
plot(b1,'r')
title('原始信号');
axis([0 100*length(s) -0.1 1.1]);
grid on;
subplot(212);
plot(fsk)
title('2FSK信号');
grid on;
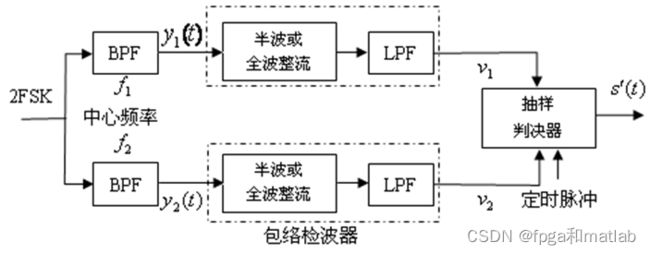
数字调频信号的解调方法很多,下面仅就相干检测法、非相干检测法进行介绍。2FSK信号的包络检波法解调方框图如图所示,其可视为由两路2ASK解调电路组成。
包络检波法:
非相干解调不需要与载波同频同相的参考信号,因此实现起来更为简单。常见的非相干解调方法有鉴频器法、过零检测法和差分检测法等。这些方法都是基于检测FSK信号频率变化来实现解调的。例如,鉴频器法通过检测FSK信号的瞬时频率变化并将其转换为幅度变化来恢复基带信号;过零检测法通过检测FSK信号过零点的数量或间隔来判断数字信息;差分检测法则利用相邻码元之间的频率变化来恢复基带信号。非相干解调的性能略低于相干解调,但在许多实际应用中仍然被广泛使用。
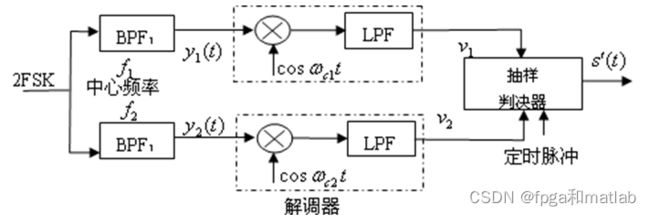
相干检测法:
相干解调需要使用与载波同频同相的参考信号。通过将接收到的FSK信号与两个参考信号(频率为f1和f2)分别相乘,然后经过低通滤波器滤除高频成分,可以得到两个基带信号。通过比较这两个基带信号的幅度或相位差异,可以判断接收到的数字信息是“1”还是“0”。相干解调具有较高的性能,但要求严格的同步和相位匹配。相干检测的具体解调电路是同步检波器,原理方框图如图7所示。图中两个带通滤波器的作用同于包络检波法,起分路作用。
3.PSK
绝对相移是利用载波的相位(指初相)直接表示数字信号的相移方式。二进制相移键控中,通常用相位0和pi来分别表示“0”或“1”。2PSK已调信号的时域表达式为
相干解调需要使用与载波同频同相的参考信号。通过将接收到的PSK信号与参考信号相乘,可以消除载波的相位变化,得到一个包含原始数字信息的基带信号。然后,通过抽样、判决等步骤,可以从基带信号中恢复出原始的数字信息。相干解调具有较高的性能,但要求严格的同步和相位匹配。
非相干解调不需要与载波同频同相的参考信号,而是直接利用PSK信号的相位信息进行解调。常见的非相干解调方法包括差分编码和差分解码。在这种方法中,发送端在发送每个符号之前先对前一个符号的相位进行差分编码,接收端则通过检测相邻符号之间的相位差来恢复原始数字信息。非相干解调的性能略低于相干解调,但在某些特定场景下(如快速变化的信道或无法获取精确同步的场景)可能更为适用。
MATLAB简要程序如下:
t=0:2*pi/99:2*pi;
m1=[];
c1=[];
b1=[];
for n=1:length(s)
if s(n)==0;
m=-ones(1,100);
b=zeros(1,100)
else s(n)==1;
m=ones(1,100);
b=ones(1,100)
end
c=sin(f*t);
m1=[m1 m];
c1=[c1 c]
b1=[b1 b];
end
psk=c1.*m1;
subplot(211);
plot(b1)
title('原始信号');
axis([0 100*length(s) -0.2 1.1]);
subplot(212);
plot(psk);
title('PSK信号');
grid on;
ASK、FSK和PSK是数字通信中三种基本的调制方法。每种方法都有其优点和缺点,适用于不同的应用场景。ASK实现简单,但抗噪声性能较差;FSK具有较好的抗噪声性能,但需要较宽的频带;PSK具有较高的频谱效率,但对同步要求较高。在实际应用中,需要根据具体需求选择合适的调制方式。