【第二十二课】最短路：bellman_ford / spfa算法 (acwing-851 / acwing-853 / c++代码)

目录

前言

acwing-853

bellman_ford算法的思想

代码如下

一些解释

acwing-851

spfa算法思想

代码如下

一些解释 

---

前言

由于权重可以表示不同的度量，例如距离、时间、费用等，具体取决于问题的背景，因此会存在一些权值为负数的题目。也就是存在负权边的最短路问题。

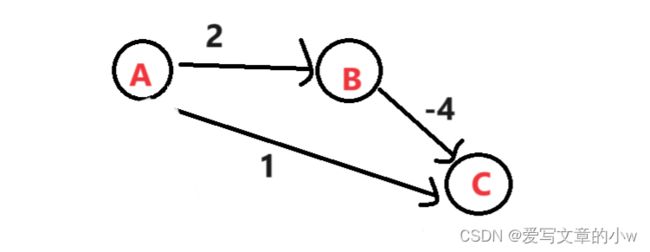
dijkstra算法由于每次都选择当前最短路径的节点进行扩展，并不能解决带有负权值的最短路问题。会存在如下图这样的问题

根据dijkstra的算法思路，我们会先确定A->C的最短路径是1，但其实，A可以先到B再到C ，这样最短距离是-2.

于是有了bellman_ford算法和SPFA算法专门解决有负权值的最短路问题。

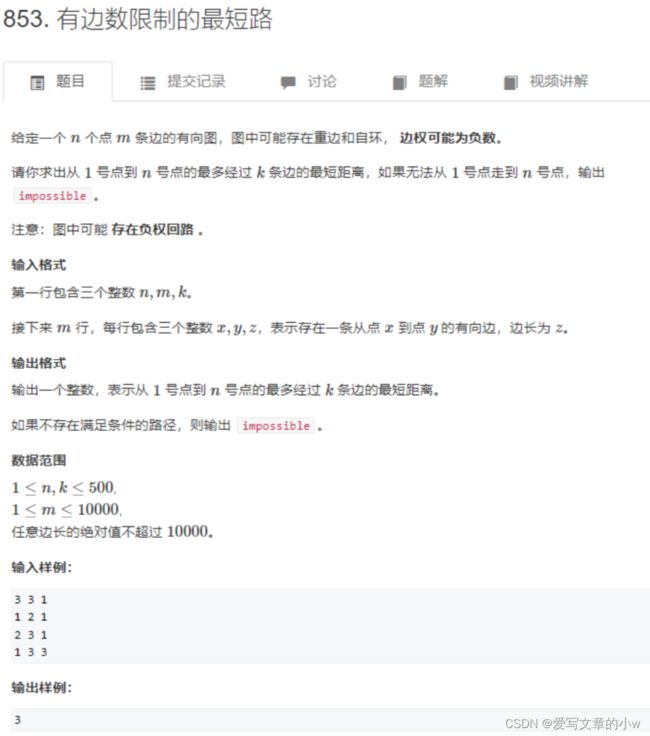
acwing-853

对于有负权边的有边数限制的最短路问题，只能用 bellman_ford算法 解决。

bellman_ford算法的思想

通过迭代逼近从源节点到其他所有节点的最短路径。

也就是我们并没有像dijkstra算法一样 直接一次找到当前直连的最短的就不在管这个点，即使之后再发现负权边，也没办法再更新了，

而是通过有限制的迭代次数，尽可能的找到最短距离。

我们迭代的内容就是：遍历所有的边，通过松弛操作更新该点最短距离。松弛操作也就是下面这段代码的内容，只是个名字而已知道就好

dist[v] = min(dist[v], dist[u] + weight(u, v));

这里需要注意的就是：可能我们A点进行了dist数组的更新，我们的更新就是通过加了一条边实现的，那么在同一轮迭代中的后续更新，可能会使用前面的更新之后的结果，这样就可能导致一条路径上的边被计算了多次，从而违反了最多只能经过k条边的限制。

因此我们要创建一个backup数组，每次迭代之前就将初始的dist数组复制到backup里，这样每次在这个备份上进行更新，就可以确保每个节点在当前轮次中只受到一次更新的影响，而不受到之前已经更新的影响。

该算法适用于带有负权边的图，并且能够检测负权环的存在。

如何检测负权环的呢？

一般需要在算法执行完毕后，再进行额外的检查。通常，检查方法是再进行一轮迭代，如果某个节点的最短路径在这一轮仍然被更新，那么就说明存在负权环。

代码如下

#include
#include
#include
using namespace std;
const int N=510,M=10010;
int n,m,k;

int dist[N],backup[N];
struct Edge{
    int a,b,w;
}edges[M];
int bellmain_ford()
{
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;
    // k 次迭代可以确保在有限次迭代内 找到从源节点到其他节点的最短路径
    for(int i=0;i0x3f3f3f3f/2)return -1;
    return dist[n];
}
int main()
{
    cin>>n>>m>>k;

    for(int i=0;i

一些解释

1.在这道题的代码中，我们并没有进行负权环的检测。

2.最后是否存在最短距离的判断中

if(dist[n]>0x3f3f3f3f/2)return -1;

我们用0x3f3f3f3f/2作为判断标准是因为

可能有负权值导致最后的结果不等于0x3f3f3f3f，但是也是无限接近于无穷大的，因此dist[n] > 0x3f3f3f3f / 2就可以认为是无穷大了。

这个可以了解一下：

.

我们经常需要一个表示“无穷大”的值，特别是在图论和动态规划等领域。0x3f3f3f3f是一个常用的表示无穷大的值，因为它是一个非常大的正整数。

.

如果你在计算过程中需要将两个“无穷大”的值相加，那么结果可能会超过整数的最大值，导致溢出。这就是为什么在一些情况下，我们会使用0x3f3f3f3f / 2作为无穷大的表示，以避免溢出的问题。 

关于这些解释，我没太明白，欢迎交流指点 

疑问

还有这道题在输入数据的时候，我使用while循环就会出错

    int i=0;
    while(m--)
    {
        int x,y,z;
        cin>>x>>y>>z;
        edges[i++]={x,y,z};
    }

就是代码其他部分都一样，只有输入数据这里用了while循环，结果就执行不对了，也欢迎指点 

acwing-851

spfa算法可以解决大部分的带负权值甚至全为正值的图的最短路问题。

spfa算法思想

spfa是对bellman_ford算法的优化。主要优化的地方就在遍历每条边进行松弛操作

for(int j=0;j

bellman_ford算法每次迭代都对所有边无差别的进行松弛操作，然鹅我们很容易发现只有当上一次a为顶点 backup[a] 有了更短距离的更改时，以a为顶点指出的顶点才会有距离的更改。

spfa针对这一点进行了优化：利用队列，将每次更改距离的点入队，每次出队一个点，遍历这个点所直连的点，进行距离的判断更改。

代码如下

#include
#include
#include
#include
using namespace std;
const int N=1e5+10;
int n,m;
int h[N],e[N],ne[N],w[N],idx;
int dist[N];
bool st[N];
void add(int a,int b,int c)
{
    e[idx]=b;
    ne[idx]=h[a];
    w[idx]=c;
    h[a]=idx++;
}
int spfa()
{
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;
    queue q;
    q.push(1);
    st[1]=1;
    while(q.size())
    {
        int t=q.front();
        q.pop();
        st[t]=0;
        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(dist[j]>dist[t]+w[i])
            {
                dist[j]=dist[t]+w[i];
                if(!st[j])
                {
                    q.push(j);
                    st[j]=1;
                }
            }
        }
    }
    if(dist[n]==0x3f3f3f3f)return -1;
    return dist[n];
}
int main()
{
    cin>>n>>m;
    memset(h,-1,sizeof h);
    while(m--)
    {
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c);
    }
    int t=spfa();
    if(t==-1)puts("impossible");
    else cout<

这段代码在理解算法思想之后，比较好理解。 

一些解释 

1.st数组

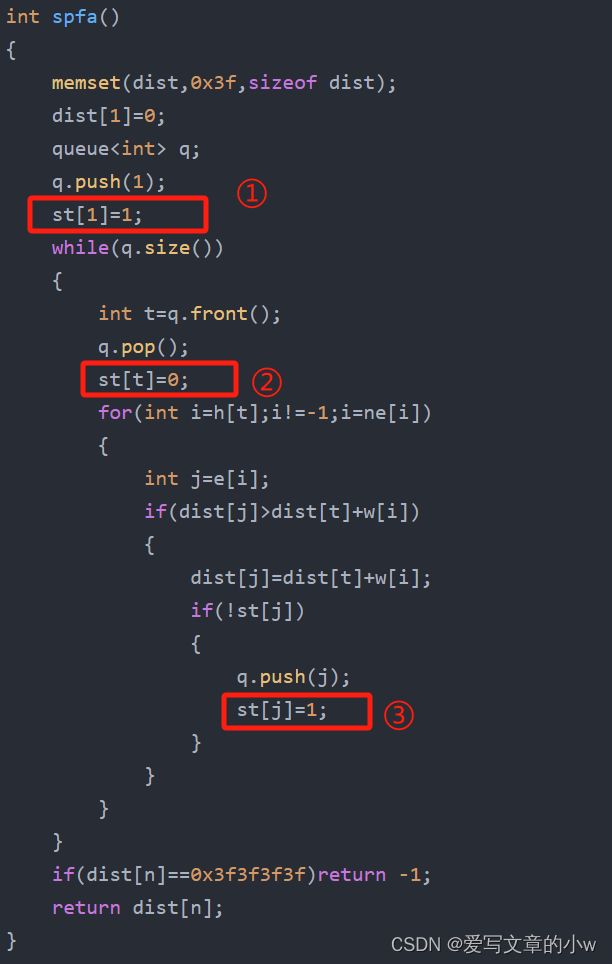
在代码中，我们有三处关于st数组的代码

①就是初始状态，先把源点入队，并将其st值置为1，表示在队列中。

②我们每次对一个点执行操作的时候，将该点出队了，因此先置为0

③每个更新了距离的节点会被入队，因此置为1

我最开始比较疑惑的是②那里。应该是因为之前写的st数组都没有在那样的位置置0的

但是我们要明白这里，st数组的作用是什么。

st数组用于跟踪每个节点是否在队列中。当我们将一个节点加入队列时，我们就将st对应的值设为1。当我们从队列中取出一个节点时，我们就将st对应的值设为0。

在算法的执行过程中，由于节点可能会多次进入和离开队列，我们需要在每次从队列中取出节点时更新st数组。

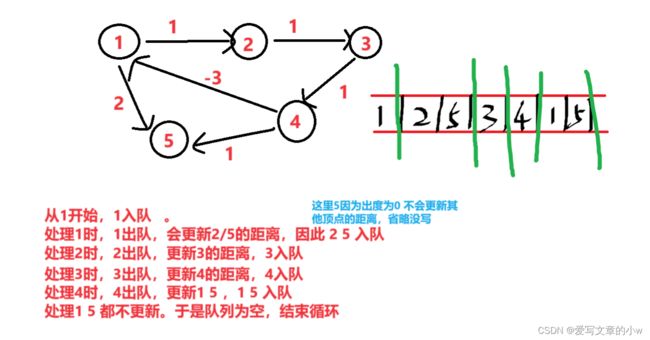
下面图中举个例子看一下算法执行的过程，就能更清楚这里所说的，节点可能会多次入队出队，②处代码的作用也更清晰了~

2.时间复杂度

---

先写到这里，，早日恢复状态！！

有问题欢迎指出，一起加油！！！