Python数据科学：Scikit-Learn机器学习

4.1Scikit-Learn机器学习

Scikit-Learn使用的数据表示：二维网格数据表

实例1：通过Seaborn导入数据

def skLearn():

    '''

    scikit Learn基本介绍

    :return:

    '''

    import seaborn as sns

    #导入Iris数据集

    #注：一般网络访问不了

    iris = sns.load_dataset('iris')

    iris.head()

实例2：通过本地导入数据

def skLearn1():

    '''

    本地导入csv数据

    :return:

    '''

    df_iris = pd.read_csv('./data/Iris.csv')

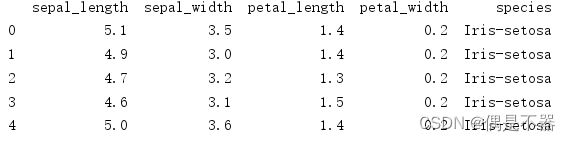
    print(df_iris.head())

鸢尾花数据集说明：

sepal_length:萼片长度

sepal_width:萼片宽度

petal_length:花瓣长度

petal_width:花瓣宽度

species:鸢尾花类型，Iris-setosa(山鸢尾)，Iris-versicolor(变色鸢尾)，Iris-virginica(维吉尼亚鸢尾)

df_iris.head()

样本：鸢尾花数据集矩阵，矩阵的行n_samples；

特征：某些数据参数的列称为特征，特征列数n_features,鸢尾花数据集需要去掉species列；

特征矩阵：数据集的特征列矩阵，一般用X表示。维度为[n_samples,n_features]。

目标数组：一个标签或目标数组，一般为一维数组，一般用y表示。长度为n_samples。

实例3：构建特征矩阵，目标数组

def skLearn1():

    '''

    本地导入csv数据

    :return:

    '''

    df_iris = pd.read_csv('./data/Iris.csv')

    print(df_iris.head())

    #获取数据集行列

    print(df_iris.shape)



    #构建特征矩阵

    X_iris = df_iris.drop('species',axis=1)

    #构建目标数组

    y_iris = df_iris['species']



    #使用seaborn绘制图片

    sns.set()

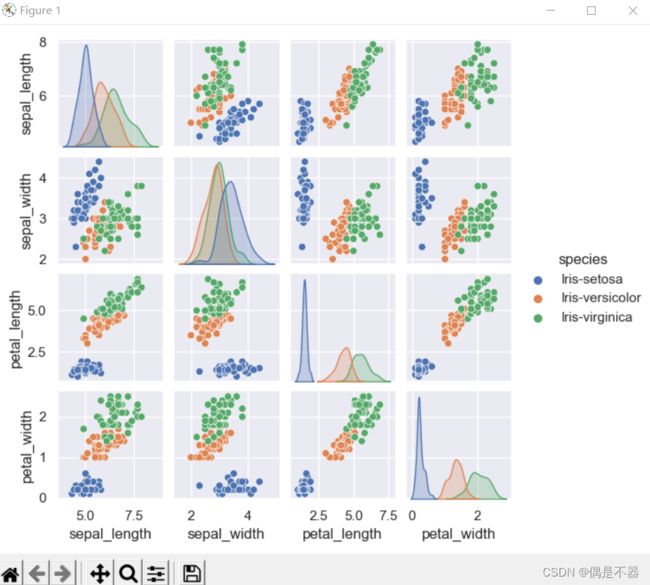
    sns.pairplot(df_iris,hue='species',height=1.5)

    plt.show()

通过sns.pairplot绘制不同特征值相关性图。

对角线上是单一特征值之间，不同鸢尾花种类在该特征值上数据的重叠程度。

Scikit-Learn的评估器API:

1. 通过Scikit-Learn中导入合适的评估器类，选择模型类；
2. 选择合适数值对模型类实例化；
3. 整理数据，获取特征矩阵，目标数组；
4. 调用模型fit()方法，对数据进行拟合
5. 对新的数据应用模型：有监督学习模型中使用predict()方法，无监督学习使用transform()或predict()方法。

实例4：构建机器学习有监督学习模型，对鸢尾花进行识别

def skLearn2():

    '''

    有监督学习，鸢尾花分类

    :return:

    '''

    #读取数据

    df_iris = pd.read_csv('./data/Iris.csv')

    #构建特征矩阵

    X_iris = df_iris.drop('species',axis=1)

    #构建目标数组

    y_iris = df_iris['species']

    #划分训练集，测试集

    from sklearn.model_selection import train_test_split

    Xtrain,Xtest,ytrain,ytest = train_test_split(X_iris,y_iris,random_state=1)



    #选择模型

    #高斯朴素贝叶斯

    from sklearn.naive_bayes import GaussianNB

    model = GaussianNB()

    #训练模型

    model.fit(Xtrain,ytrain)

    #使用模型对数据进行预测

    y_model = model.predict(Xtest)

    #如何验证y_model数据准确性？

    #和实际的数据进行比较，确定模型预测准确率

    from sklearn.metrics import accuracy_score

    #ytest:实际数据

    #y_model:模型预测数据

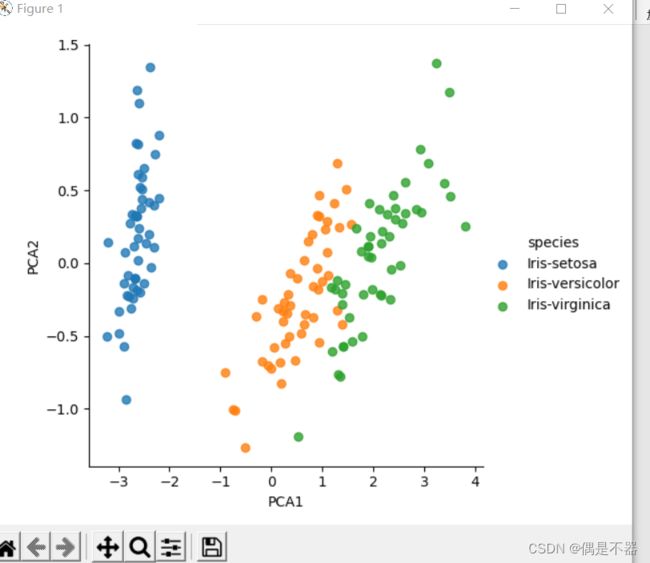
    print(accuracy_score(ytest,y_model))

实例5：无监督学习，鸢尾花数据降维

鸢尾花数据集有四个特征维度，对数据进行降维，保留数据的本质特征，用低维度矩阵表示高维数据。

def skLearn3():

    '''

    无监督学习，鸢尾花数据降维

    :return:

    '''

    #读取数据

    df_iris = pd.read_csv('./data/Iris.csv')

    #构建特征矩阵

    X_iris = df_iris.drop('species',axis=1)

    #构建目标数组

    y_iris = df_iris['species']

    #选择模型

    #主成分分析PCA,快速线性降维

    from sklearn.decomposition import PCA

    #设置超参数

    model = PCA(n_components=2)

    #拟合数据

    model.fit(X_iris)

    #将数据转换为二维数据

    X_2d = model.transform(X_iris)

    #将数据插入原数据

    df_iris['PCA1'] = X_2d[:,0]

    df_iris['PCA2'] = X_2d[:,1]

    print(df_iris)

    #sns绘制二维数据投影图

    sns.lmplot("PCA1","PCA2",hue='species',data=df_iris,fit_reg=False)

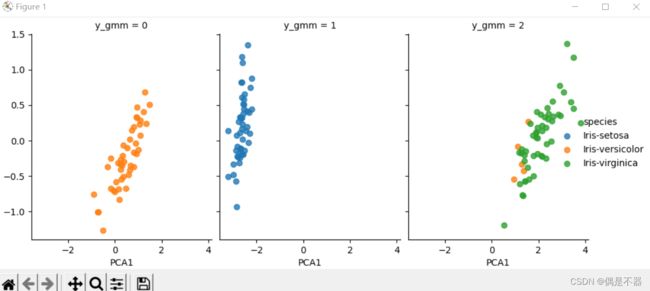
    plt.show()

实例6：无监督学习，对鸢尾花数据进行聚类分析

def skLearn4():

    '''

    无监督学习，在降维后数据基础上，聚类分析

    高斯混合模型

    :return:

    '''

    #读取数据

    df_iris = pd.read_csv('./data/Iris.csv')

    #构建特征矩阵

    X_iris = df_iris.drop('species',axis=1)

    #构建目标数组

    y_iris = df_iris['species']



    #选择模型

    #主成分分析PCA,快速线性降维

    from sklearn.decomposition import PCA

    #设置超参数

    model_pca = PCA(n_components=2)

    #拟合数据

    model_pca.fit(X_iris)

    #将数据转换为二维数据

    X_2d = model_pca.transform(X_iris)

    #将数据插入原数据

    df_iris['PCA1'] = X_2d[:,0]

    df_iris['PCA2'] = X_2d[:,1]



    #选择模型

    #高斯混合模型GMM

    from sklearn.mixture import GaussianMixture

    #设置超参数

    model = GaussianMixture(n_components=3,covariance_type='full')

    #拟合数据

    model.fit(X_iris)

    #预测数据

    y_model = model.predict(X_iris)



    #将预测数据放入原数据

    df_iris['y_gmm'] = y_model

    #绘制图片

    sns.lmplot("PCA1","PCA2",data=df_iris,hue='species',col='y_gmm',fit_reg=False)

    plt.show()

实例7：手写数字识别

步骤1：获取手写数字集，查看数据

def skLearn5():

    '''

    手写数字探索

    :return:

    '''

    #加载手写数字集

    from sklearn.datasets import load_digits

    digits = load_digits()

    #(1798,8,8)

    #一共1798个样本，8x8的像素

    print(digits.images.shape)



    #绘制手写数据图

    fig,axes = plt.subplots(10,10,figsize=(8,8))

    for i,ax in enumerate(axes.flat):

        #显示图片手写数字

        ax.imshow(digits.images[i],cmap='binary',interpolation='nearest')

        #显示目标数字

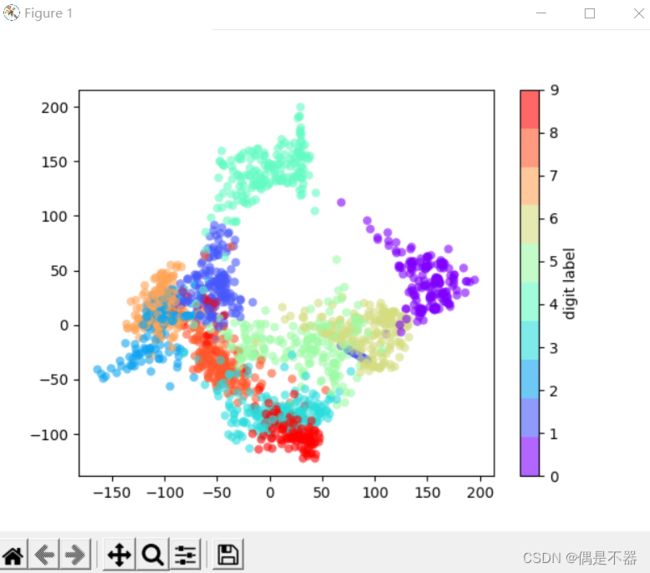
        ax.text(0.05,0.05,str(digits.target[i]),transform=ax.transAxes,color='blue')

步骤2：将数据进行降维处理,查看降维后数据。可以发现还是有许多数字之间是重叠的。

#8x8矩阵相当于64个特征值

#获取特征矩阵

X_digits = digits.data

#获取目标列

y_digits = digits.target



#64维的特征值进行降维处理,流形学习算法

from sklearn.manifold import Isomap

#降到二维

iso = Isomap(n_components=2)

#拟合数据

iso.fit(X_digits)

#获取转换后的数据

X_trans = iso.transform(X_digits)

#显示二维数据

plt.scatter(X_trans[:,0],X_trans[:,1],c=y_digits,edgecolor='none',alpha=0.6,cmap=plt.cm.get_cmap('rainbow',10))

plt.colorbar(label='digit label',ticks=range(10))

步骤3：使用高斯朴素贝叶斯模型训练识别模型。使用混淆矩阵判断模型识别效果

#训练模型，数字识别

#划分训练集，测试集

from sklearn.model_selection import train_test_split

Xtrain,Xtest,ytrain,ytest = train_test_split(X_trans,y_digits,random_state=0)

#使用模型

from sklearn.naive_bayes import GaussianNB

model = GaussianNB()

#训练数据

model.fit(Xtrain,ytrain)

#预测测试数据

y_model = model.predict(Xtest)

#获取识别准确率

from sklearn.metrics import accuracy_score

#识别率有70*

print(accuracy_score(ytest,y_model))



#如何知道模型识别的不足？

#使用混淆矩阵

from sklearn.metrics import confusion_matrix

mat = confusion_matrix(ytest,y_model)

print(mat)

#绘制热力图

sns.heatmap(mat,square=True,annot=True,cbar=False)

plt.xlabel('predict value')

plt.ylabel('true value')

从图像可以看出，识别数字2时，许多识别成了7或者1；识别5时，也识别错误成其他数字