实验3:数值计算实验
实验3:数值计算实验
3.1 基础训练
- 方程求根
编程调用fzero求解方程 2 x 3 − 3 x 2 + 4 x − 5 = 0 2x^3-3x^2+4x-5=0 2x3−3x2+4x−5=0的实数根,并将所求根赋给变量xp,编写一个函数调用fzero,并返回xp.
解:求一阶导,得 6 x 2 + 6 x + 4 > 0 6x^2+6x+4>0 6x2+6x+4>0,故至多只有一个实数根,不妨求 x 0 = 1 x_0=1 x0=1附近的实数根。
函数代码如下:
function xp = root
f = @(x)(2*x.^3-3*x.^2+4*x-5);
xp = fzero(f,1);
end
- 请用Euler法求解下列微分方程:
{ d y d t = 0.02 ( 1 − 0.001 y ) y , y ( 0 ) = 10 \begin{cases}\frac{\mathrm{d}y}{\mathrm{d} t }=0.02(1-0.001y)y,\\y(0)=10\end{cases} {dtdy=0.02(1−0.001y)y,y(0)=10
并将Euler求解结果与Matlab的ode23函数求解结果绘图进行对比.
注:先写出Euler法迭代公式,再编程实现.
解:
Euler函数文件代码:
function [t,y] = odeEuler (diffeq,tn,h,y0)
t = (0:h:tn)';
n = length(t);
y = y0 * ones(n,1);
for k =2:n;
y (k) = y(k-1) + h*feval(diffeq,t(k-1),y(k-1));
end
函数文件:
function dfun = fun1(t,y)
dfun = 0.02*(1-0.01*y).*y;
end
脚本文件:
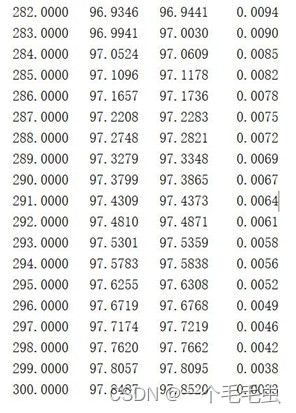
[t1,y1] = odeEuler(@fun1,300,1,10)
[t2,y2] = ode23(@fun1,[0:300],10)
plot(t1,y1,'r',t2,y2,'b')
legend('odeEuler','ode23')
wc = abs(y1-y2);
all = [t1,y1,y2,wc];
disp(all)
第一列为t,第二列为欧拉法求得函数值,第三列为ode23求得函数值,第四列为两者误差.
- 二次多项式拟合
某种产品在生产过程中的性能指标y与它所含的某种材料的含量x有关,现将试验所得16组数据记录列于下表.
| x | 20.05 | 22.09 | 24.13 | 26.24 | 28.11 | 30.29 | 32.09 | 34.23 |
|---|---|---|---|---|---|---|---|---|
| y | 26.5 | 10.46 | 2.75 | 3.53 | 11.67 | 29.98 | 52.26 | 87.19 |
| x | 36.23 | 38.2 | 40.27 | 42.27 | 44.07 | 46.05 | 48.47 | 50.08 |
| y | 128.11 | 176.24 | 235.17 | 300.25 | 365.66 | 445.1 | 552.84 | 631 |
要求拟合y与x的函数关系。用多项式拟合函数polyfit进行二次多项式拟合。编写函数文件返回2个参数:
第1个返回参数为二次多项式系数组成的行向量p(元素由高次到低次排列);
第2个返回参数为拟合函数在点x=25:0.4:60处的函数值(用1个行向量表示).
程序文件第1行参考格式如下:
function [p,v]= myfun
解:考虑数据录入不方便,故将表格数据命名为’data.xlsx’文件并保存在同一目录下;
函数代码:
function [p,v]= myfun
filename = 'data.xlsx'; % Excel 文件名或路径
sheet = 'Sheet1'; % 工作表名
range1 = 'B1:Q1'; % 读取的数据范围
range2 = 'B2:Q2'
[x, txt1, raw1] = xlsread(filename, sheet, range1);
[y, txt2, raw2] = xlsread(filename, sheet, range2);
p = polyfit(x,y,2);
x0 = 25:0.4:60;
v = polyval(p,x0);
运行结果:
- 分别用符号运算和数值计算命令quad求积分 ∫ 0 π 2 c o s x 1 + s i n 2 x d x \int_0^{\frac{\pi}{2}}\frac{cosx}{1+sin^2x}\,dx ∫02π1+sin2xcosxdx
代码:
syms y(x)
y = cos(x)./(1+(sin(x)).^2);
f1 = int(y,x,0,pi/2) %符号计算
fun = @(x) cos(x)./(1+sin(x).^2);
f2 = quad(fun, 0, pi/2) %数值计算
3.2 综合训练
一、实验任务
请用Matlab函数ode23求解下列微分方程:
{ d 2 x d t 2 = 20 ( 1 − x 2 ) d x d t + 0.5 x , x ( 0 ) = 2 , x ′ = 0 \begin{cases}\frac{d^2x}{dt^2}=20(1-x^2)\frac{dx}{dt}+0.5x,\\x(0)=2,\qquad x^{'}=0 \end{cases} {dt2d2x=20(1−x2)dtdx+0.5x,x(0)=2,x′=0
将上述二阶方程转化为一阶微分方程组;编写函数调用ode工具箱函数返回x在点0:0.1:100处的函数值,用列向量存储这些函数值,并绘制出函数x在区间[0,100]上的曲线。此列向量为double型数组.
二、 实验目的
熟悉二阶微分方程转化为一阶微分方程组的方法,熟悉Matlab解微分方程数值解的函数.
三、实验过程
首先,将原二阶微分方程转化为一阶微分方程组,令 x 1 = x , x 2 = d x d t x1=x,x_2=\frac{dx}{dt} x1=x,x2=dtdx则
{ d x 1 d t = x 2 d x 2 d t = 20 ( 1 − x 1 2 ) x 2 + 0.5 x 1 x 1 ( 0 ) = 2 , x 2 ( 0 ) = 0 \begin{cases}{\frac{dx_1}{dt}=x_2} \\ \frac{dx_2}{dt}=20(1-x_1^2)x_2+0.5x_1 \\ x_1(0)=2,x_2(0)=0 \end{cases} ⎩ ⎨ ⎧dtdx1=x2dtdx2=20(1−x12)x2+0.5x1x1(0)=2,x2(0)=0
代码:
x0 = [2;0];
tn = [0:0.1:100];
[t,x] = ode23(@vdpol,tn,x0)
plot(t,x(:,1))
xlabel('t');ylabel('x');
function dfun = vdpol(t,x)
dfun = [x(2);20*(1-x(1)^2)*x(2)+0.5*x(1)];
end
部分运行结果:
四、实验自评与改进方向
在本次实验中,较好地完成了各项实验任务,进一步巩固了数学实验方法,对各个常用函数有了更深的理解。以后应该多多练习,深入理解ode23,int等系统函数的使用方法,提高数学实验能力。
五、实验体会,收获及建议
在处理数据时,使用了xlsread函数来读取xlsx文件中的数据,从而不用手动输入,大大提高了工作效率。在处理更大量的数据时,使用类似的函数将达到事半功倍的效果。