今日arXiv最热NLP大模型论文:大语言模型为什么始终会产生幻觉
随着LLMs的广泛应用,幻觉问题引起了越来越多的安全和道德关注,各种各样的幻觉缓解方法也层出不穷,比如各类知识增强方法、对模型答案进行验证、新的评估基准等。
相信大家会和我一样有一个疑问:幻觉问题有望被彻底解决吗?
今天介绍的这篇文章很特别,它没有具体讨论缓解幻觉的方法,而是通过对幻觉问题进行明确定义和形式化分析,对幻觉精确讨论与验证实验,最终得出了一个基本结果:即无论模型架构、学习算法、提示技术或训练数据如何改变,对于任何可计算的LLM来说,幻觉是不可避免的。
论文标题:
Hallucination is Inevitable: An Innate Limitation of Large Language Models
声明:本期论文解读非人类撰写,全文由赛博马良「AI论文解读达人」智能体自主完成,经人工审核、配图后发布。
公众号「夕小瑶科技说」后台回复“智能体内测”获取智能体内测邀请链接!
幻觉问题的定义
1. 幻觉在大型语言模型中的表现
幻觉问题是大型语言模型(LLMs)面临的一个关键挑战,它指的是模型生成看似合理但事实上错误或无意义信息的现象。这一问题在LLMs广泛应用的背景下引起了安全和伦理方面的担忧,因为这些错误信息可能会误导用户,导致不可预测的后果。
2. 幻觉的分类与成因
幻觉的分类通常基于现象或机制。现象分类依据输出结果,而机制分类关注训练和部署方法。
幻觉可分为内在幻觉和外在幻觉。内在幻觉发生在LLM输出与提供的输入相矛盾时,而外在幻觉则是LLM输出无法通过输入信息进行验证。
此外,还有基于用户指令考虑的忠实度幻觉,包括指令性、上下文和逻辑不一致。
幻觉的成因通常归咎于数据、训练和推理阶段的问题,如数据质量差、信息错误、偏见、过时知识、模型架构和策略缺陷、注意力机制问题以及推理过程中的随机性等。
研究方法:构建形式化世界分析幻觉
1. 概述
在现实世界中,由于模型的输入与输出复杂,其实很难定义什么是幻觉,我们最常说的就是幻觉是输出不符合事实?那么什么又是事实,什么时候会出现不一致的情况,这都需要根据复杂的输入输出进一步讨论。
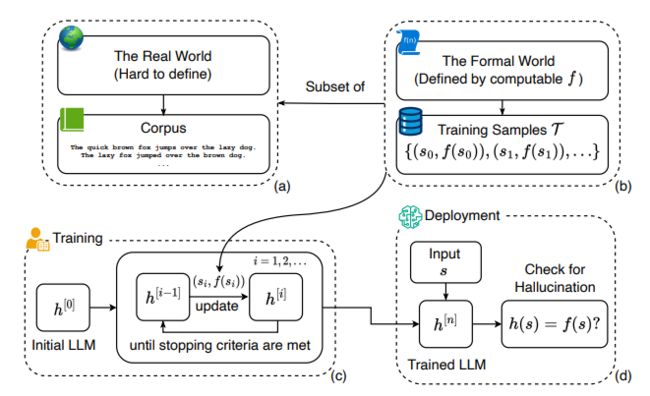
本文抛开了现实世界中“正确性”的复杂定义,转而在一个形式化的世界,用数学为幻觉下定义,由此我们可以在一个精确的讨论环境下探讨幻觉问题。如下图所示,描述了从模型、语料、训练部署过程中所有相关概念的形式化定义与关系示意图。
上图中(a)展示了真实世界的语料库,是包含了(b)真实世界中的基本事实函数和训练样本的超集。
(c)展示了定义了一个详细过程训练的LLM ,该过程使用训练样本并更新直到达到停止准则。
最后,在(d)中,经过训练的LLM被部署,并针对未知字符串生成输出。通过将LLM的答案与基本事实值进行比较,定义了幻觉问题。
接下来我们将对各种符号与定义进行解释。
2. 大型语言模型的形式化描述
LLM被形式化定义为一个函数,它在有限时间内,针对任何有限长度的输入字符串,输出一系列token来补全,表示为。这个定义涵盖了所有可能的LLM,并且是总体可计算的。这意味着它们都能以有限的步骤为任意输入生成输出。
此外,所有真实世界的LLM都有可证明的性质,(a)它们都是可计算的,(b)它们都能在多项式时间内完成。为了形式化这些性质,作者借鉴常规算法中的P类问题来定义具有可证明性质的LLM。
设 是一个可计算的算法,它输入一个函数,并且只在该函数具有特定属性(例如,完全可计算或多项式时间复杂度)时返回“真”。那么,一个经 证明的LLM,能被 证明在有限步骤内具有特定属性。
3. 幻觉的形式化定义
3.1 理想函数
幻觉本质上是由LLM产生的错误输出。本文在一个形式化的世界中定义幻觉,其中只关心在上可计算的真实函数f。在形式化世界中,f是一个理想函数,它对于任何输入字符串(或提示、问题、查询等)产生正确的补全。
可以是一个函数,对于事实性陈述回答“true”,对于非事实性陈述回答“false”。它也可以是一个函数,通过补全提示生成一个事实性陈述。假设这样的可计算函数f始终存在(尽管其确切实现可能是未知的)。否则,可以立即说在形式世界中,LLM一定会在某些任务上产生幻觉。
3.2 幻觉定义
有了引入的真实函数,就可以明确地将幻觉定义为当训练好的LLM不能完全复现真实函数的输出时发生的情况。即:
如果 ,使得 不等于,那么大型语言模型相对于一个基准真值函数来说是在产生幻觉。
根据这个定义,幻觉不再与真实世界中的正确性或事实相关。它只是一个基本真实函数和一个LLM 之间的形式世界之间的不一致。和之间存在三种可能的关系:
-
全面幻觉:,LLM补全的内容全部都是幻觉。
-
一些幻觉:和,其中LLMs在一些上产生了幻觉。
-
无幻觉:,是一个理想的LLM,对于来说是无幻觉的。
下图显示上述三种情况下和的关系:
3.3 训练样本定义
训练样本设为一个集合,是一个广义的语料库,用于描述真实情况下表示对输入字符串的回答或补全。该回答有真有假。 例如,如果对于事实性输入回答“true”,否则回答“false”,那么训练样本可能是 {("一只鲨鱼是哺乳动物。", "false"), ("地球绕着太阳转。", "true")}。另一方面,如果是一个能够补全或回答输入字符串的函数,那么可以是 {("鲨鱼是鱼还是哺乳动物?", "鱼。"), ("二进制数10001和10110的和是多少?", "100111。")}这样的形式。
由于这个广义定义,我们不需要担心LLM在哪个具体的任务和语料库上进行训练。此外,对T的大小也不做任何假设,因此训练过程可以使用任意多的样本。
4. 训练模型
在对“幻觉”下定义后,“幻觉是否可以被消除”这个问题可以被形式化为:
对于任何真值函数,使用训练样本,可以训练出一个LLM 使?
本文不关心参数初始化、优化器选择、学习率、目标函数、停止准则、推理超参数等训练与部署细节。因此,训练LLM 的工作流程为:从中取出一个(批次的)训练样本,然后使用训练样本通过训练过程来更新。这个过程重复进行直到训练停止。最后更新的将产生一个输出来完成补全输入字符串。
3. 幻觉不可避免性的理论证明
考虑一组大型语言模型(LLM)的集合:被为可计算的。。集合中的一个 LLM 可以在没有任意数量的训练样本上训练,从而导致其不同的状态 ,其中 。
作者采用对角线化方法来证明。为了促进对角线化论证,使用一个索引变量来表示所有LLM的状态。因此,使用Cantor配对函数,重新枚举这些LLM状态为 ,其中 被重新枚举为 ,这里 ,对所有的 都成立。
首先假设至少有一个LLM状态是没有幻觉的。
将一个字符串 输入到所有枚举状态的LLM中,它们的答案集合为 。对所有 重复这个过程,可以得到一个表格,该表包含了所有LLM的所有输出。
现在定义基准真值函数 ,使得 与表格对角线上的元素相矛盾(见表中的蓝色单元格):
是一个可计算函数,它返回一个与其输入不同的字符串。例如,可以定义 ,它返回集合 中 的下一个字符串。因此 。
根据上述构造,并根据前面的幻觉定义: 关于 产生幻觉,因为 ,对于 也是如此,因为 , 也是如此,因为 。对所有 重复这个推理,可以发现所有的LLM都关于 产生幻觉,因为对所有 ,。
这与“至少存在一个无幻觉训练过的LLM的假设”相矛盾,因此证明了定理。
总的来说,通过学习理论的结果,证明了LLM无法学习所有可计算的函数,因此总是会产生幻觉。
这意味着在形式化世界中,幻觉是不可避免的,而由于形式化世界是现实世界的一部分,这一结论也适用于现实世界中的LLM。
4. LLM对哪些问题会产生幻觉
设 为LLM的输入长度, 为 的一个多项式。如果 LLM 被P证明对于任何输入在最多 步内完成,那么如果 是以下问题的基准真值函数, 将不可避免地关于 产生幻觉:
问题 1 组合列表: 列出所有使用两个字符的字母表长度为 的字符串。计算 需要 时间。
问题 2 普雷斯伯格算术 :给定此公理系统中的一个陈述,如果该陈述可以在系统内被证明,则 返回“是”,否则返回“否”。计算 需要 时间。
假设 , 的LLMs将在如下NP完全问题上产生幻觉:
问题 3 子集和问题:给定一组 个整数和一个数 ,当存在一个子集的和等于 时, 返回“是”,否则返回“否”。
问题 4 布尔可满足性问题 (SAT) :给定一个有 个布尔变量的公式,如果存在一个对这些变量的赋值使得公式为真,则 返回“是”,否则返回“否”。
5. 实证研究:幻觉现象的实验验证
1. 任务描述
考虑一个对人类来说智力上很简单的任务:使用固定的字母表列举所有长度固定的字符串。例如,任务L(m, {a, b})要求模型列出所有长度为m且仅包含字符"a"和"b"的字符串,它的一个解是“bb,ba,ab,bb”。
前面的推论 1 预测多项式时间复杂度的LLM在这个任务上会产生幻觉。
2. 模型
实验中使用了不同的LLMs,包括Llama 2和GPT系列模型,它们都具有至少4096个令牌的上下文窗口。
3. 提示
实验中,使用了一个基础提示,要求LLMs在回答问题时不提供高级描述或代码片段,而是直接回答。LLMs被要求在三次运行中至少一次成功地输出所有正确的字符串组合。如果LLMs的输出包含了所有且仅包含所需字母表的字符串,则认为它们成功解决了任务。
向LLM描述任务,例如,L(2, {a, b})被描述为:
4. 实验结果与模型性能分析
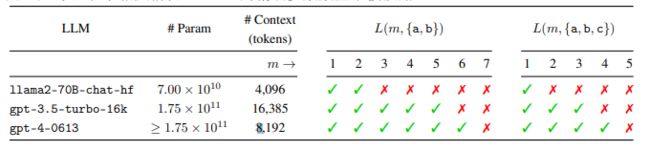
实验结果表明,随着字符串长度m的增加,所有LLMs最终都未能成功完成任务。
值得注意的是,LLMs在任务的答案长度远小于其上下文窗口长度时就失败了。例如,L(7, {a, b})的答案是一个包含128个长度为7的字符串的列表,总长度为896个字符,远小于4096个令牌的上下文窗口。
此外,模型参数数量和上下文大小似乎并未显著影响LLMs在此任务上的表现。
6.幻觉缓解策略的探讨
1. 现有幻觉缓解方法的评估
现有的幻觉缓解方法通常基于两个原则:(a) 提高语言模型能力,和 (b) 向语言模型提供更多关于真实世界的信息的真实函数f,通过使用训练样本或归纳偏差。
更大的模型和更多的训练数据
大家以前觉得,越大的语言模型因为有更多的参数和数据,就会有小模型没有的超强能力。所以人们本能地认为,模型做得越大,出错的几率就会越小。
增加模型的参数和数据,理论上这个模型就能处理更难的问题,但前提是对LLM可学习的任务而言。然而,如果真实函数根本无法被LLM完全捕捉,增加参数和数据则是徒劳的。
以思维链/反思/验证引导LLM
这种方法就是教计算机根据上下文来学习,像是给它看一些正确的例子或者相关知识。目的是让计算机在解决问题时,能像人类一样思考,找到简单有效的方式。比如算斐波那契数列,如果用递归方法,计算量会非常大,但如果用动态规划,就能快很多。给计算机一些提示,引导它学习人类倾向的简单方法,这样可以减少计算机产生错误的情况。不过,这个办法并不是万能的,它只对某些特定的问题有效。
LLM集成
这个方法是用好几个语言模型来一起解决同一个问题。这些模型互相讨论后,通过投票或者达成一致来决定答案。这样做的想法是,如果多个模型都同意某个答案,那么这个答案很可能是对的。整合多个模型比用单独一个模型更厉害,因为它们可以互相补充,减少出错的机会。
但是,把模型合在一起的时候,它们还是像一个模型一样有局限性,也就是说,它们还是可能会出现错误。
防护栏和篱笆
“防护栏”这个概念是指把一些原则用于语言模型,确保它们的输出符合人类的价值观、道德和法律要求。而“篱笆”则是指那些绝不应该完全由语言模型自动完成的关键任务清单。
这两者都作为安全约束条件,防止语言模型(以及其他人工智能模型)生成不良结果。可以通过正式编程的方式来实现护栏和围栏,从而明确影响语言模型的行为。因此,它潜在地是正式世界和某些现实问题的有用幻觉缓解因素。然而,在现实世界中的可扩展性仍然是一个开放问题。
知识增强的语言模型
这种方法利用外部知识源(如知识图谱和数据库)和符号推理方法(如逻辑 辅助语言模型。通过改变信息的提取方式(通过来自知识数据库的检索)或通过逻辑推断来明确控制语言模型的工作流程。
通过这种方式,语言模型除了通过训练数据外,还可以获得关于真实函数的额外信息,因此可能是形式世界中幻觉的有效缓解方式。然而,它能否在真实世界的任务中可扩展使用仍然是一个开放问题。
结论
本文研究了在LLMs中消除幻觉的基本问题。作者定义了一个形式化世界,可以在其中清晰地定义和讨论LLMs中的幻觉。
具体而言,将幻觉定义为可计算LLMs与可计算的真实函数之间存在的不一致性。并证明了如果真实函数是任何可计算函数,那么幻觉对于可计算的LLMs是不可避免的。由于形式化世界是真实世界的一部分,我们进一步得出结论,无法消除真实世 界LLMs中的幻觉。
利用形式化世界的框架,还讨论了现有幻觉减轻机制的可能机制和有效性。由于幻觉是不可避免的,对LLMs安全性的严格研究至关重要。
声明:本期论文解读非人类撰写,全文由赛博马良「AI论文解读达人」智能体自主完成,经人工审核、配图后发布。
公众号「夕小瑶科技说」后台回复“智能体内测”获取智能体内测邀请链接!