矩阵迹（trace）, 行列式（determinate）

1. 迹（trace）

矩阵的迹（trace）表示矩阵 A AA 主对角线所有元素的和

迹的来源

最根本的应该就是迹和特征值的和相等。因为特征值如此重要，所以才定义了迹。离开了这一点，我觉得迹也就失去了立足点。

迹与特征值

一直在用迹等于特征值的和来求特征值，但从来没有想过二者究竟是怎么联系起来的。没事儿就重新推了一遍。

一元二次方程的根与系数的关系

先看一元二次方程。

推广至一元n次方程

特征值

分开来写就是：

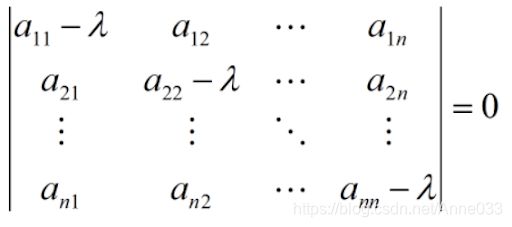
其实质也是一个以$\lambda$为未知数的一元n次方程。展开后可以得到如下的形式：
${\lambda }^n+(a_{11}+a_{22}+\cdots +a_{nn}){\lambda }^{n-1}+a_{11}{a}_{22}\cdots a_{nn}+\cdots =0$
从而可以得到$\lambda$的所有解的和等于$(a_{11}+a22+\cdots +a_{nn})$。也就是矩阵的特征值的和等于矩阵的迹。

2. 行列式（determinant）

矩阵 A AA 的行列式值记为 $det(A)$。


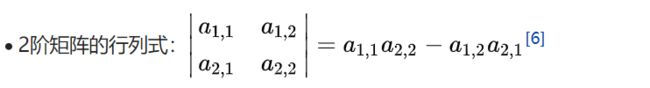
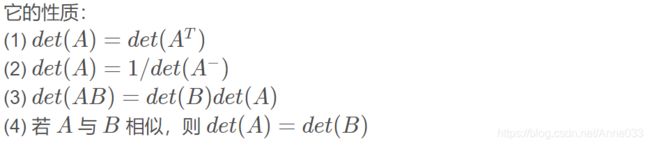
行列式对一个2x2的矩阵来说就是一个 平行四边形, 在四个边沿自己的方向变化时，这个平行四边形的面积就会变化。

扩展到3x3的矩阵，那行列式 就是一个 平行六面体，同样的，在每个边沿自己的方向变化的时候，这个平行六面体的体积就会变化。

3. 迹与行列式的关系

迹可以理解为行列式的导数，所以也就表示了在每个边沿自己的方向变化时，该平行四边形的面积或者平行六面体的体积变化的大小。这实际上和特征值非常相关，迹是特征值的和，行列式是特征值的积。

4. 如何理解矩阵的迹

确实，“迹”就是线性变换藏在矩阵中痕迹。

上面那幅图还有个有意思的地方，用了金、篆、隶、楷来写“迹”字，虽然各有千秋，却又“相似”，彷佛在暗示，线代中的“迹”反映出矩阵“相似”这个特征。

本文准备如下来讲解：
什么是线性变换？
同一个线性变换在不同基下的矩阵，就是相似矩阵
相似矩阵的“迹”都相等
相似矩阵的“迹”、行列式、特征值的关系

a. 什么是线性变换

http://www.360doc.com/content/18/0208/09/15930282_728535853.shtml


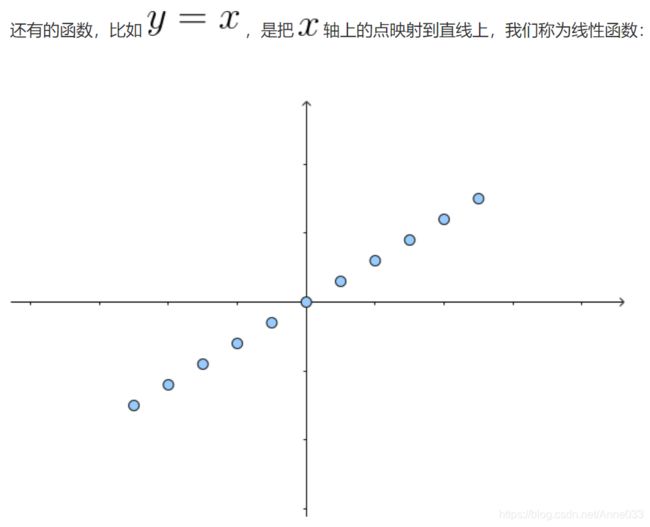
这其实也是线性函数，只是一般我们把这称为线性变换。

综合上面两点，其实，所谓矩阵就是指定基下的线性变换。

b. 同一个线性变换在不同基下的矩阵，就是相似矩阵

之前提到的线性变换，为了示意整个平面的点都被变换了，我用下面的淡蓝色网格来表示这个线性变换（增加一个参考点$x$方便观察）：

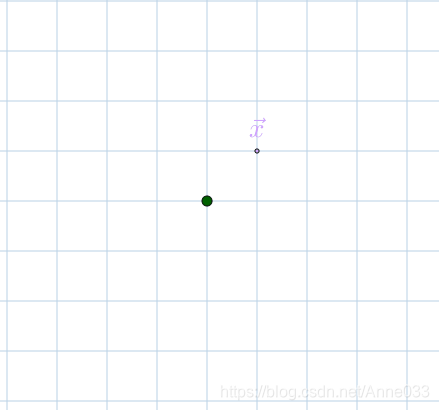
可见，这就是一个围绕蓝点旋转的线性变换，并且作为文章作者，我可以准确的告诉你，所有的点旋转了 弧度（蓝点，即中心点也可以认为旋转了 弧度）。

我们来看看不同基下的矩阵是什么样子的。

下面我会给出所有具体的数字，你可以去计算一下，省得说我骗你。

b.1 标准正交基下的矩阵 A

如何理解矩阵的乘法？https://mp.weixin.qq.com/s?__biz=MzIyMTU0NDMyNA==&mid=2247487771&idx=1&sn=af57d5d9f60ac742e17aa77c8226f30e&chksm=e83a7bf0df4df2e67c323669e537a7e74267c53652c6b9312c401c717a9fd0c2836eba718fff&scene=21#wechat_redirect

b.2 另外一个基下的矩阵

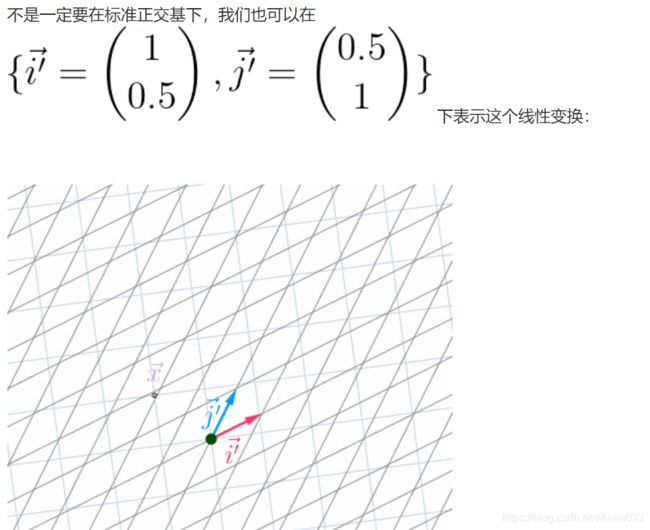
可见淡蓝色网格代表的线性变换是没有发生变化的，只是基不一样了。

矩阵具体计算出来就是：

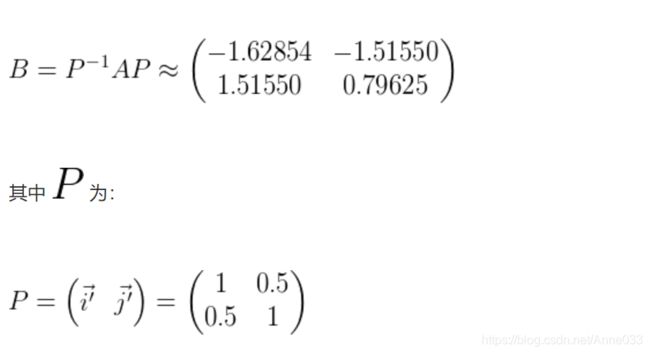
为什么这么计算，就请查看如何理解相似矩阵这篇文章了。
https://mp.weixin.qq.com/s?__biz=MzIyMTU0NDMyNA==&mid=2247486892&idx=1&sn=5c2529222992792248b1c9a0d950b6ec&chksm=e83a6747df4dee519d8f0b546ff231711a8d847adc28f1120452f87c58c256962bc3a2988e93&scene=21#wechat_redirect

b.3 相似矩阵

c 相似矩阵的“迹”都相等

这个线性变换，悄悄在这两个相似矩阵A、B中留下了痕迹，就是它们的主对角线之和相等：

主对角线之和因此称为“迹”。

从另外一个观点来看，我们也可以认为“迹”与坐标无关，也可以说“迹”是相似不变量。

d 相似矩阵的“迹”、行列式、特征值的关系

d.1 行列式

因为A、B代表同一个线性变换，而根据行列式的意义，行列式代表的是线性变换的伸缩比例。
既然是比例，那么也和坐标无关：

行列式又是一个相似不变量。

d.2 特征值

特征值是两个复数。

你的相貌随着年岁变换，我却还能一眼认出，就是因为其中藏着特征。

什么是特征，不被变换所改变的就是特征。

迹、行列式都是相似变换中的不变量，也就是线性变换的特征，现在全部被特征值表示了出来。看来特征值这个名字名副其实啊。

e 写在最后

行列式、迹似乎都是相似不变量，为什么把“迹”叫这个名字呢？

我想或许是“迹”是对角线之和，更容易一眼看出去来吧。

在历史中为什么命名为“迹”，对于我而言已经不可考了，或许这位先哲也曾经这样思考过吧。

http://www.360doc.com/content/18/0208/09/15930282_728535853.shtml
http://chenbinpeng.com/2017/02/06/%E7%9F%A9%E9%98%B5%E7%9A%84%E8%BF%B9/
https://blog.csdn.net/robert_chen1988/article/details/88576194