SPOJ 375 Query on a tree(线段树维护树链剖分)
题目链接:http://www.spoj.com/problems/QTREE/
题意:给出一个树,两种操作:(1)修改某条边的权值;(2)询问某两个顶点之间边的最大值。
思路:树的路径剖分和线段树维护路径剖分。
(1)轻边和重边:记Size(U)表示以U为根的子树的结点个数。令V为U的儿子中Size(V)最大的一个,那么我们称边(U,V)为重边,其余边为轻边。
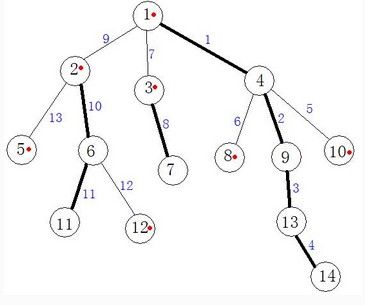
如上图,粗边为重边,细边为轻边。
(2)树链:将所有的重边连起来得到若干条链,这些链叫做树链。上图中红点标记的点为每条树链的头。单独一个节点自己组成一个树链。
(3)下面我们讲如何得到树链。步骤是进行两次DFS,第一次DFS,得到如下数组:dep[u]u的深度,son[u]<u,son[u]>为重边,father[u]u的父节点。第二次DFS建立树链,得到如下数组:w[u]:<father[u],u>这条边在线段树中的位置为w[u]。如上图所示,一条树链中的边在线段树中是连续的一段,top[u]u在树链中的头,上图中top[1]=top[4]=top[9]=top[13]=top[14]=1,top[2]=top[6]=top[11]=2。
(4)单点操作:比如题目中的第一种操作。这种操作比较简单,直接在线段树中找到这个点直接更新即可。
(5)成段操作:比如成段更新或查询等。我们拿10和11作为例子说明。首先,我们得到u=10和v=11的top值,分别是f1=10和f2=2,发现f1的dep值大,则更新图中的边5;接着u=4,f1=1,此时f2的深度的,则更新图中的边9、10和11,接着v=1,f1=1,退出。
有了这些,本题就比较容易了。
vector<int> g[N];
int dep[N],w[N],father[N],top[N],son[N],size[N];
int E[N][3],root,n,z;
int tree[N<<2];
void DFS1(int u)
{
size[u]=1; son[u]=0;
int i,v;
FOR0(i,SZ(g[u]))
{
v=g[u][i];
if(v==father[u]) continue;
father[v]=u;
dep[v]=dep[u]+1;
DFS1(v);
if(size[v]>size[son[u]]) son[u]=v;
size[u]+=size[v];
}
}
void DFS2(int u,int root)
{
w[u]=++z; top[u]=root;
if(son[u]) DFS2(son[u],root);
int i,v;
FOR0(i,SZ(g[u]))
{
v=g[u][i];
if(v!=son[u]&&v!=father[u]) DFS2(v,v);
}
}
void build(int t,int L,int R,int pos,int x)
{
if(L==R)
{
tree[t]=x;
return;
}
int mid=(L+R)>>1;
if(pos<=mid) build(t*2,L,mid,pos,x);
else build(t*2+1,mid+1,R,pos,x);
tree[t]=max(tree[t*2],tree[t*2+1]);
}
int get(int t,int L,int R,int l,int r)
{
if(L==l&&R==r) return tree[t];
int mid=(L+R)>>1;
if(r<=mid) return get(t*2,L,mid,l,r);
if(l>mid) return get(t*2+1,mid+1,R,l,r);
int x=get(t*2,L,mid,l,mid);
int y=get(t*2+1,mid+1,R,mid+1,r);
return max(x,y);
}
int query(int a,int b)
{
int f1=top[a],f2=top[b],ans=0,temp;
while(f1!=f2)
{
if(dep[f1]<dep[f2]) swap(f1,f2),swap(a,b);
temp=get(1,1,z,w[f1],w[a]);
if(temp>ans) ans=temp;
a=father[f1];
f1=top[a];
}
if(a==b) return ans;
if(dep[a]>dep[b]) swap(a,b);
temp=get(1,1,z,w[son[a]],w[b]);
if(temp>ans) ans=temp;
return ans;
}
int main()
{
rush()
{
RD(n); root=(n+1)>>1; father[root]=0; z=0; dep[root]=0;
int i;
FOR1(i,n) g[i].clear();
FOR1(i,n-1)
{
RD(E[i][0],E[i][1],E[i][2]);
g[E[i][0]].pb(E[i][1]);
g[E[i][1]].pb(E[i][0]);
}
DFS1(root); DFS2(root,root);
FOR1(i,n-1)
{
if(dep[E[i][0]]>dep[E[i][1]]) swap(E[i][0],E[i][1]);
build(1,1,z,w[E[i][1]],E[i][2]);
}
char op[10];
int x,y;
while(RD(op),op[0]!='D')
{
RD(x,y);
if(op[0]=='Q') PR(query(x,y));
else build(1,1,z,w[E[x][1]],y);
}
}
}