视觉slam十四讲学习笔记（六）视觉里程计 1

本文关注基于特征点方式的视觉里程计算法。将介绍什么是特征点，如何提取和匹配特征点，以及如何根据配对的特征点估计相机运动。

目录

前言

一、特征点法

1 特征点

2 ORB 特征

FAST 关键点

BRIEF 描述子

3 特征匹配

二、实践：特征提取和匹配

三、2D-2D: 对极几何

1 对极约束

2 本质矩阵

3 单应矩阵

四、实践：对极约束求解相机运动

五、三角测量

总结

---

前言

1. 理解图像特征点的意义, 并掌握在单幅图像中提取出特征点，及多幅图像中匹配特征点的方法。

2. 理解对极几何的原理，利用对极几何的约束，恢复出图像之间的摄像机的三维运动。

3. 理解 PNP 问题，及利用已知三维结构与图像的对应关系，求解摄像机的三维运动。

4. 理解 ICP 问题，及利用点云的匹配关系，求解摄像机的三维运动。

5. 理解如何通过三角化，获得二维图像上对应点的三维结构。

哔哩哔哩课程链接：视觉SLAM十四讲ch7_1_哔哩哔哩_bilibili

---

一、特征点法

特征点法通常是指在计算机视觉和图像处理中使用的一种方法，其目的是检测和描述图像中的关键特征点。这些特征点可以是图像中独特或显著的位置，如角点、边缘点等，它们在不同图像中具有相似性，因此可以用来进行图像匹配、目标跟踪、三维重建等应用。

特征点法的一般步骤包括以下几个方面：

1. 特征点检测： 通过一些算法检测图像中的关键特征点，这些特征点通常是在局部区域内显著的位置，例如角点、边缘点等。常用的特征点检测算法包括Harris角点检测、Shi-Tomasi角点检测、SIFT（尺度不变特征变换）、SURF（加速鲁棒特征）等。

2. 特征点描述： 对于检测到的特征点，需要提取其特征描述子，以便后续匹配。这些描述子通常是能够表征特征点周围局部结构的向量或矩阵。常用的特征描述算法包括SIFT描述子、SURF描述子、ORB（Oriented FAST and Rotated BRIEF）描述子等。

3. 特征点匹配： 在不同图像中，通过比较特征点的描述子，找到相似的特征点对，从而建立图像间的对应关系。匹配可以使用一些距离度量或相似性度量来完成。

4. 应用： 特征点法的应用非常广泛，包括图像配准、目标跟踪、三维重建、拼接图像、物体识别等领域。

1 特征点

VO 的主要问题是如何根据图像来估计相机运动。然而，图像本身是一个由亮度和色彩组成的矩阵，如果直接从矩阵层面考虑运动估计，将会非常困难。所以，习惯于采用这样一种做法：首先，从图像中选取比较有代表性的点。这些点在相机视角发生少量变化后会保持不变，所以会在各个图像中找到相同的点。然后，在这些点的基础上，讨论相机位姿估计问题，以及这些点的定位问题。在经典 SLAM 模型中，把它们称为路标。而在视觉 SLAM 中，路标则是指图像特征（Features）。

• 特征是图像信息的另一种数字表达形式。
• 特征点在相机运动之后保持稳定。
• 特征点是图像里一些特别的地方。

可以作为图像特征的部分：角点、边缘、区块。

人工设计的特征点能够拥有如下的性质：

1. 可重复性（Repeatability）：相同的“区域”可以在不同的图像中被找到。

2. 可区别性（Distinctiveness）：不同的“区域”有不同的表达。

3. 高效率（Efficiency）：同一图像中，特征点的数量应远小于像素的数量。

4. 本地性（Locality）：特征仅与一小片图像区域相关。

特征点由关键点（Key-point）和描述子（Descriptor）两部分组成。

比方说，当谈论 SIFT 特征时，是指“提取 SIFT 关键点，并计算 SIFT 描述子”两件事情。关键点是指该特征点在图像里的位置，有些特征点还具有朝向、大小等信息。描述子通常是一个向量，按照某种人为设计的方式，描述了该关键点周围像素的信息。描述子是按照“外观相似的特征应该有相似的描述子”的原则设计的。因此，只要两个特征点的描述子在向量空间上的距离相近，就可以认为它们是同样的特征点。

2 ORB 特征

OpenCV 提供的 ORB 特征点检测结果。

ORB 特征亦由关键点和描述子两部分组成。它的关键点称为“Oriented FAST”，是一种改进的 FAST 角点，什么是 FAST 角点我们将在下文介绍。它的描述子称为 BRIEF（Binary Robust Independent Elementary Features）。因此，提取 ORB 特征分为两个步骤：

1. FAST 角点提取：找出图像中的” 角点”。相较于原版的 FAST, ORB 中计算了特征点的主方向，为后续的 BRIEF 描述子增加了旋转不变特性。

2. BRIEF 描述子：对前一步提取出特征点的周围图像区域进行描述。

FAST 关键点

FAST（Features from Accelerated Segment Test）是一种用于快速检测图像中角点的特征点检测算法。FAST 算法主要用于实时应用，它在速度和计算效率上表现出色，并且在相对平滑的图像中能够准确地检测到关键点。

以下是 FAST 算法的主要特点和步骤：

1. 加速度段测试（Accelerated Segment Test）： FAST 算法使用一种称为加速度段测试的策略来判断一个像素是否是关键点。在这个测试中，选择了一个中心像素点和周围的16个像素点，然后根据这些像素点的灰度值与中心像素的灰度值进行比较，以判断中心像素是否是一个关键点。这个测试是基于一种简单的圆形区域的像素采样。

2. 非极大值抑制： 在加速度段测试的结果中，如果中心像素是一个关键点，就会产生一些相邻的像素点也可能被认为是关键点。为了防止重复检测，FAST 算法进行非极大值抑制，只选择那些在某个阈值下，灰度值超过相邻像素灰度值的中心像素点作为最终的关键点。

3. 参数选择： FAST 算法中有一个重要的参数，即阈值。阈值的选择影响到算法的灵敏度，可以根据具体应用场景进行调整。

FAST 算法的优点在于其计算速度快，适用于实时应用，但缺点是对图像噪声和纹理较敏感。在一些情况下，FAST 可以用于快速初始化特征点，然后通过其他方法（例如，通过机器学习方法或描述子匹配）来提高准确性。FAST 算法常常用于计算机视觉领域中的实时特征点检测，如图像拼接、物体跟踪和视觉SLAM（Simultaneous Localization and Mapping）等应用中。

FAST 是一种角点，主要检测局部像素灰度变化明显的地方，以速度快著称。它的思想是：如果一个像素与它邻域的像素差别较大（过亮或过暗）, 那它更可能是角点。相比于其他角点检测算法，FAST 只需比较像素亮度的大小，十分快捷。它的检测过程如下：

1. 在图像中选取像素 p，假设它的亮度为 Ip。

2. 设置一个阈值 T(比如 Ip 的 20%)。

3. 以像素 p 为中心, 选取半径为 3 的圆上的 16 个像素点。

4. 假如选取的圆上，有连续的 N 个点的亮度大于 Ip + T 或小于 Ip − T，那么像素 p可以被认为是特征点 (N 通常取 12，即为 FAST-12。其它常用的 N 取值为 9 和 11，他们分别被称为 FAST-9，FAST-11)。

5. 循环以上四步，对每一个像素执行相同的操作。

针对 FAST 角点不具有方向性和尺度的弱点，ORB 添加了尺度和旋转的描述。尺度不变性由构建图像金字塔，并在金字塔的每一层上检测角点来实现。而特征的旋转是由灰度质心法（Intensity Centroid）实现的。

BRIEF 描述子

BRIEF（Binary Robust Independent Elementary Features）是一种用于图像特征描述的算法。它主要用于生成图像中检测到的关键点的二进制描述子，用于在图像匹配和目标识别等任务中进行特征匹配。

以下是 BRIEF 描述子的主要特点和步骤：

1. 二进制描述子生成： BRIEF 描述子的主要思想是通过在关键点周围选择一组固定的、随机的像素对，并比较它们的灰度值来生成二进制字符串。这些比较结果被编码成二进制位，形成一个二进制向量，称为 BRIEF 描述子。

2. 随机选择的像素对： BRIEF 算法在每个关键点周围随机选择一组像素对，这些像素对的选择对于最终的描述子起到关键作用。这种随机性带来了描述子的差异性，使其更具区分性。

3. 描述子长度： BRIEF 描述子的长度由用户指定，通常为一个定长的二进制字符串。较长的描述子可能提供更好的区分性，但也需要更多的存储和计算资源。

4. 不变性： BRIEF 描述子相对于尺度和旋转是不变的。这是通过在图像尺度空间中选择随机像素对的方法实现的。

尽管 BRIEF 描述子具有计算速度快、存储需求低的优势，但它对图像噪声和干扰较为敏感。为了提高鲁棒性，通常会与其他算法一起使用，例如在关键点检测中可以与 FAST 等方法结合使用。

总体而言，BRIEF 描述子在实时图像处理和计算资源受限的场景中表现良好，特别适用于嵌入式系统和移动设备等应用。

3 特征匹配

特征匹配是视觉 SLAM 中极为关键的一步，宽泛地说，特征匹配解决了 SLAM 中的数据关联问题（data association），即确定当前看到的路标与之前看到的路标之间的对应系。通过对图像与图像，或者图像与地图之间的描述子进行准确的匹配，可以为后续的姿态估计，优化等操作减轻大量负担。然而，由于图像特征的局部特性，误匹配的情况广泛存在，而且长期以来一直没有得到有效解决，目前已经成为视觉 SLAM 中制约性能提升的一大瓶颈。部分原因是因为场景中经常存在大量的重复纹理，使得特征描述非常相似。在这种情况下，仅利用局部特征解决误匹配是非常困难的。

• 最简单的特征匹配方法就是暴力匹配（Brute-Force Matcher）。
• 描述子距离表示了两个特征之间的相似程度，不过在实际运用中还可以取不同的距离度量范数。
• 用汉明距离（Hamming distance）做为度量——两个二进制串之间的汉明距离，指的是它们不同位数的个数。
• 快速近似最近邻（ FLANN ） 算法更加适合于匹配点数量极多的情况。

二、实践：特征提取和匹配

slambook/ch7/feature_extraction.cpp

#include 
#include 
#include 
#include 

using namespace std;
using namespace cv;

int main ( int argc, char** argv )
{
    if ( argc != 3 )
    {
        cout<<"usage: feature_extraction img1 img2"< keypoints_1, keypoints_2;
    Mat descriptors_1, descriptors_2;
    Ptr detector = ORB::create();
    Ptr descriptor = ORB::create();
    // Ptr detector = FeatureDetector::create(detector_name);
    // Ptr descriptor = DescriptorExtractor::create(descriptor_name);
    Ptr matcher  = DescriptorMatcher::create ( "BruteForce-Hamming" );

    //-- 第一步:检测 Oriented FAST 角点位置
    detector->detect ( img_1,keypoints_1 );
    detector->detect ( img_2,keypoints_2 );

    //-- 第二步:根据角点位置计算 BRIEF 描述子
    descriptor->compute ( img_1, keypoints_1, descriptors_1 );
    descriptor->compute ( img_2, keypoints_2, descriptors_2 );

    Mat outimg1;
    drawKeypoints( img_1, keypoints_1, outimg1, Scalar::all(-1), DrawMatchesFlags::DEFAULT );
    imshow("ORB特征点",outimg1);

    //-- 第三步:对两幅图像中的BRIEF描述子进行匹配，使用 Hamming 距离
    vector matches;
    //BFMatcher matcher ( NORM_HAMMING );
    matcher->match ( descriptors_1, descriptors_2, matches );

    //-- 第四步:匹配点对筛选
    double min_dist=10000, max_dist=0;

    //找出所有匹配之间的最小距离和最大距离, 即是最相似的和最不相似的两组点之间的距离
    for ( int i = 0; i < descriptors_1.rows; i++ )
    {
        double dist = matches[i].distance;
        if ( dist < min_dist ) min_dist = dist;
        if ( dist > max_dist ) max_dist = dist;
    }
    
    // 仅供娱乐的写法
    min_dist = min_element( matches.begin(), matches.end(), [](const DMatch& m1, const DMatch& m2) {return m1.distancedistance;
    max_dist = max_element( matches.begin(), matches.end(), [](const DMatch& m1, const DMatch& m2) {return m1.distancedistance;

    printf ( "-- Max dist : %f \n", max_dist );
    printf ( "-- Min dist : %f \n", min_dist );

    //当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
    std::vector< DMatch > good_matches;
    for ( int i = 0; i < descriptors_1.rows; i++ )
    {
        if ( matches[i].distance <= max ( 2*min_dist, 30.0 ) )
        {
            good_matches.push_back ( matches[i] );
        }
    }

    //-- 第五步:绘制匹配结果
    Mat img_match;
    Mat img_goodmatch;
    drawMatches ( img_1, keypoints_1, img_2, keypoints_2, matches, img_match );
    drawMatches ( img_1, keypoints_1, img_2, keypoints_2, good_matches, img_goodmatch );
    imshow ( "所有匹配点对", img_match );
    imshow ( "优化后匹配点对", img_goodmatch );
    waitKey(0);

    return 0;
}

对ch7文件夹中的cmake工程进行编译，报错：

undefined reference to `vtable for fmt::v7::format_error

链接上fmt 库：

target_link_libraries("可执行文件" ${Sophus_LIBRARIES} fmt)

未筛选的匹配中带有大量的误匹配。经过一次筛选之后，匹配数量减少了许多，大多数匹配都是正确的。这里筛选的依据是汉明距离小于最小距离的两倍，这是一种工程上的经验方法。尽管在示例图像中能够筛选出正确的匹配，但仍然不能保证在所有其他图像中得到的匹配都是正确的。因此，在后面的运动估计中，还需要使用去除误匹配的算法。

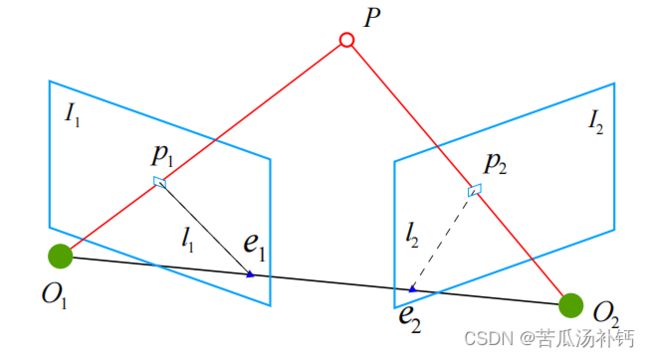
三、2D-2D: 对极几何

1 对极约束

对极约束简洁地给出了两个匹配点的空间位置关系。于是，相机位姿估计问题变为以下两步：

1. 根据配对点的像素位置，求出 E 或者 F；

2. 根据 E 或者 F，求出 R, t。

由于 E 和 F 只相差了相机内参，而内参在 SLAM 中通常是已知的，所以实践当中往往使用形式更简单的 E。我们以 E 为例，介绍上面两个问题如何求解。

2 本质矩阵

根据定义，本质矩阵 E = t ∧R。它是一个 3 × 3 的矩阵，内有 9 个未知数。那么，是不是任意一个 3 × 3 的矩阵都可以被当成本质矩阵呢？从 E 的构造方式上看，有以下值得注意的地方：

• 本质矩阵是由对极约束定义的。由于对极约束是等式为零的约束，所以对 E 乘以任意非零常数后，对极约束依然满足。把这件事情称为 E 在不同尺度下是等价的。

• 根据 E = t ∧R，可以证明 [3]，本质矩阵 E 的奇异值必定是 [σ, σ, 0]T 的形式。这称为本质矩阵的内在性质。

• 另一方面，由于平移和旋转各有三个自由度，故 t ∧R 共有六个自由度。但由于尺度等价性，故 E 实际上有五个自由度。

E 具有五个自由度的事实，表明我们最少可以用五对点来求解 E。但是，E 的内在性质是一种非线性性质，在求解线性方程时会带来麻烦，因此，也可以只考虑它的尺度等价性，使用八对点来估计 E——这就是经典的八点法（Eight-point-algorithm）。八点法只利用了 E 的线性性质，因此可以在线性代数框架下求解。

3 单应矩阵

除了基本矩阵和本质矩阵，还有一种称为单应矩阵（Homography）H 的东西，它描述了两个平面之间的映射关系。

四、实践：对极约束求解相机运动

五、三角测量

三角化获得地图点深度

---

总结

本文内容结束，关于实践部分，预计后续更新！