【吴恩达·机器学习】第二章：单变量线性回归模型（代价函数、梯度下降、学习率、batch）

• 博主简介：努力学习的22级计算机科学与技术本科生一枚
• 博主主页： @Yaoyao2024
• 每日一言: 勇敢的人，不是不落泪的人，而是愿意含着泪继续奔跑的人。
  ——《朗读者》
  

0、声明

本系列博客文章是博主本人根据吴恩达老师2022年的机器学习课程所学而写，主要包括老师的核心讲义和自己的理解。在上完课后对课程内容进行回顾和整合，从而加深自己对知识的理解，也方便自己以及后续的同学们复习和回顾。

• 课程地址2022吴恩达机器学习Deeplearning.ai课程
• 课程资料和代码（jupyter notebook)2022-Machine-Learning-Specialization

由于课程使用英文授课，所以博客中的表达也会用到英文，会用到中文辅助理解。

Machine learning specialization课程共分为三部分

• 第一部分：Supervised Machine Learning: Regression and Classification
• 第二部分：Advanced Learning Algorithms（Neural networks、Decision Trees)
• 第三部分：Unsupervised Learning: Recommenders, Reinforcement Learning

最后，感谢吴恩达老师Andrew Ng的无私奉献，和视频搬运同学以及课程资料整合同学的无私付出。Cheers!

前言

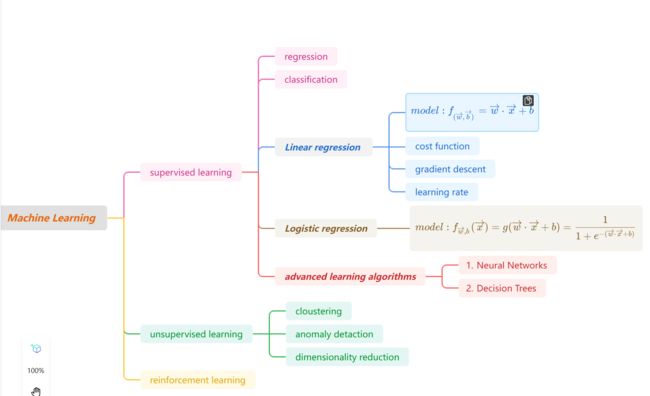
 第一章我们了解了监督学习和非监督学习，接下来我们将依次进行学习。监督学习任务主要有两个：回归和分类。回归问题的基础算法是：线性回归模型（linear regression)。这一章将对 单变量线性回归(linear regression with one varible)进行全面的学习，进而在下一章的多变量线性回归(multiple linear regression)模型中能更好的类比和掌握。

‍♀️在这一章你将掌握

• 单变量线性模型（build with an model which establish the relationship between features and target)
• 代价函数(provide a measure how well your models work on your training data/your predictions match your training data)
• 梯度下降：一种利用代价函数用来训练模型的算法
• 学习率：通过改变学习率从而影响梯度下降

接下来让我们开始吧！

1、单变量线性回归模型

首先我们要弄清楚单变量线性回归是什么，是做什么的。

• "回归”：对应的是监督学习中的“回归问题”对应的“回归模型（regression model)”，即预测连续的值。
  
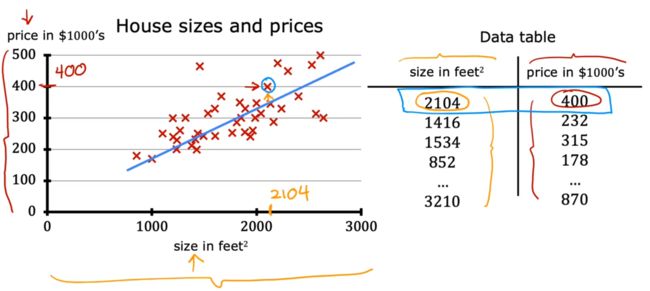
• “单变量”：是值输入数据x是单个数据。即：输入一个变量x，对应一个预测值y.比如在下图示例中，输入房间大小size，即可得到连续的房价预测值price。
  

1.1：术语(notation/terminology)

关于单变量模型中的符号约定及其解释见下图

1.2：原理（流程）

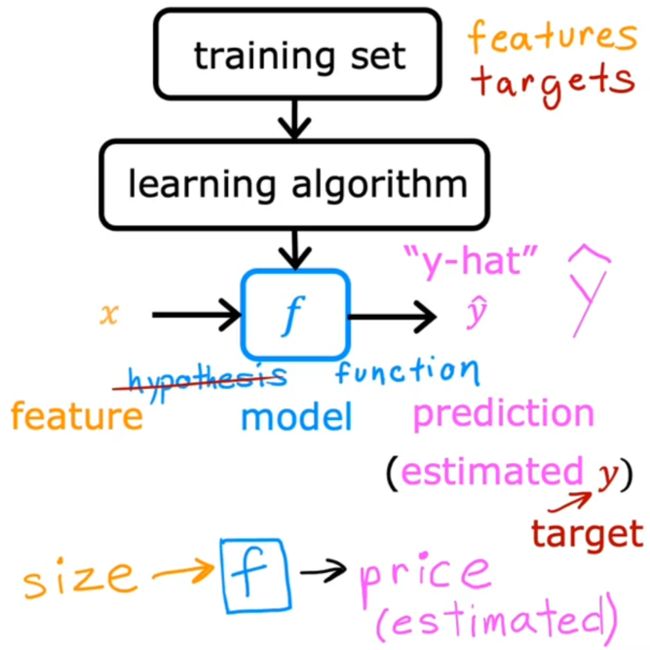
• 1、模型的训练：

  • Step1:首先，通过现有收集的数据，我们将其构建模型训练集（training set).
  • Step2：然后通过机器学习算法（learning algorithm)，利用现有的数据，训练回归模型：regression model

• 2、预测：

  • Step1:输入变量，通过模型进行计算
  • Step2:输出连续的预测结果
    

1.3：模型的表示

如果只是知道上述原理后，我们一定还不清楚，这个模型model到底是什么东西，它是如何表示的，又是如何根据输入变量进行预测的呢？我们下面一起来看看它的真实面目！

可以看到，线性模型的表示本身是一个线性函数。单变量线性回归模型对应的就是单变量的线性函数。输入数据x，经过函数计算（其实就像模型预测），得到函数输出值（也就是预测值）y

1.4：模型的预测

通过上面的学习，我们知道，一旦模型的参数w和b确定了，那么模型确定，给定输入数据x即可预测得到y

w = 200                         
b = 100    
x_i = 1.2
cost_1200sqft = w * x_i + b    

print(f"${cost_1200sqft:.0f} thousand dollars")

但是，问题在于：如何选择参数w、b，使得模型能更好的进行预测，准确率高！

再直白些：我们当然不能人工的去手动确定w,b，这就违背了机器学习让机器自己学习的本质了。我们要让模型自己去学习，也就是：模型的训练。

二、模型的训练

模型训练的本质就是：如何确定参数w、b，使得模型能更好的进行预测。

机器学习对于训练单变量模型（也就是确定w,b）有自己的训练方法，或者称为：learning algorithm——梯度下降（Gradient_Descent）.

具体如何进行的呢？还要从代价函数讲起。

2.1：代价函数

The cost equation provides a measure of how well your predictions match your training data.
也就是说，代价函数是衡量当前模型与训练数据拟合程度的一个函数。

从下图可以看出，不同的w和b拟合的函数(也就是模型）不同，对训练数据的拟合程度也不同。代价函数就是这么一个衡量模型是否和训练数据拟合的好的一个函数。

我们的目的是找到与训练数据拟合的好（当然不能过拟合）的这样一个模型。怎么找先不说，首先我们就需要学会代价函数——判断模型和数据的拟合程度。

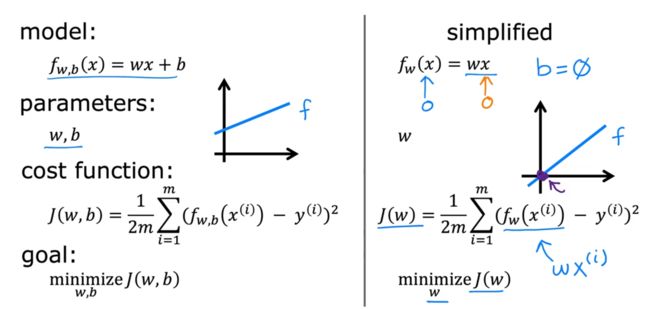
2.1.1：公式(平方误差）

‍♀️公式解析

• 1/m：保证平均，否则代价函数会随着数据量的增大而增大，没有可比性
• 1/2:主要是为了之后算梯度的时候求导好算（把2消掉）

Tips:平方误差函数是常用的代价函数，实际上还有很多种代价函数，以适用于不同的问题）

2.1.2：理解代价函数

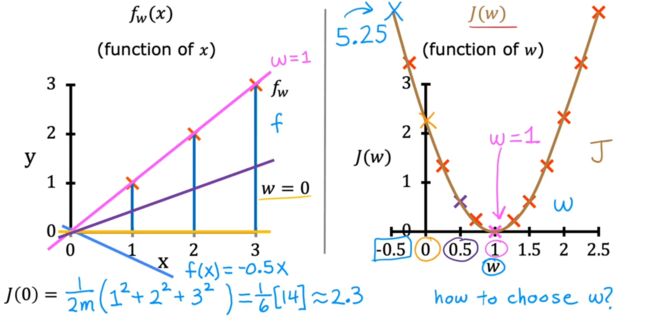
由下图可以看到，我们的目标(goal)是 最小化代价函数，从而使模型和训练数据最贴近。

而学习了代价函数的公式我们知道，代价函数是关于参数w和b的一个二元函数（这里我们为了简化问题，不去考虑b，也就是我们认为这里的代价函数是一个一元函数）

通过下图可以看到，代价函数越小，模型与数据越贴近；代价函数越大，模型与训练数据越不贴近

2.1.3：代价函数的可视化

可以看到当考虑到参数b后，代价函数的3-D可视化图像如下所示。我们的目标就是找到代价函数中的最低点

此外，除了用3-D图的表示方法，我们还可以使用下面等高线这种2-D形式来表示：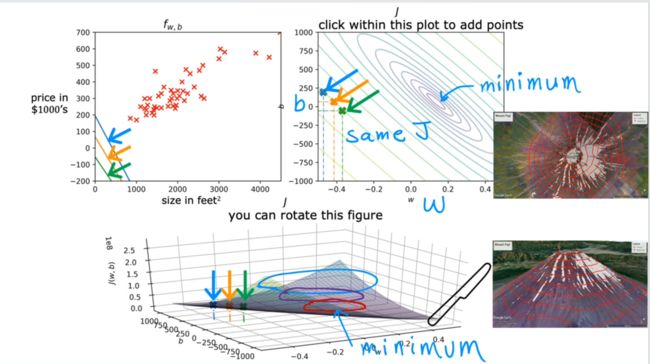

2.2：梯度下降算法

通过上面的学习，我们知道，想要得到效果最好的、与训练数据拟合最好的模型，关键是找到代价函数图像中最低的那点。

如何找到最低点呢？——梯度下降算法（gradient descent)

梯度下降算法不仅仅是用在线性回归任务中，在更多复杂的模型（如神经网络）中也有应用

下面我们具体看看这个算法的思想和步骤以及特性。

2.2.1：算法思想

把代价函数想象成下面这样一个3D立体图，像一个山坡一样。 任意选一个w和b就代表任意站在一点。

• Step1: 站在一点，环顾四周360°，选择最陡下降方向
• Step2：沿着这个方向，迈出一小步
• Step3：重复上述两个步骤
• Step4：直到局部最低点(达到收敛,converge)

特性：最终到达哪个局部最低点与起点有关。

2.2.2：数学公式

梯度下降是上述形象的下坡过程，实际上就是w和b的不断重新赋值更新，直到达到代价函数最低点的过程。

1. 偏导数项：决定了你要选择的那个最陡峭的下降方向
2. α:学习率；决定了每次你确定好方向后要走多大一步

2.2.3：计算梯度

对于后面的多变量线性回归，只需要把对应的标量换成向量即可，公式是相同的。

2.2.4：理解

下面是对公式的直观理解。

导数项总是决定下降方向，学习率α决定了沿这个方向走多远。

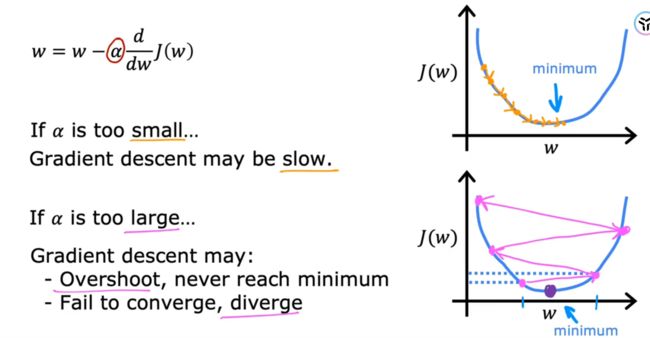
2.2.5:学习率

上面可知，梯度下降算法的关键在于两点：方向、步长

方向由导数项确定，代价函数确定了即可求。而步长——学习率，需要认为设定（属于模型训练过程中的超参数.

下图可以看到，当学习率较小时，梯度下降算法会进行的比较慢，耗时；当学习率过大时，梯度下降时来回震荡，又很难得到收敛。

如何选择学习率（也就是传说中的调参）会在下一篇文章中讲到。此处只是一个介绍。
而且这里的学习率就是全局学习率，只有一个值。后面讲卷积神经网络中还会讲到其他能自动调节学习率的方法。

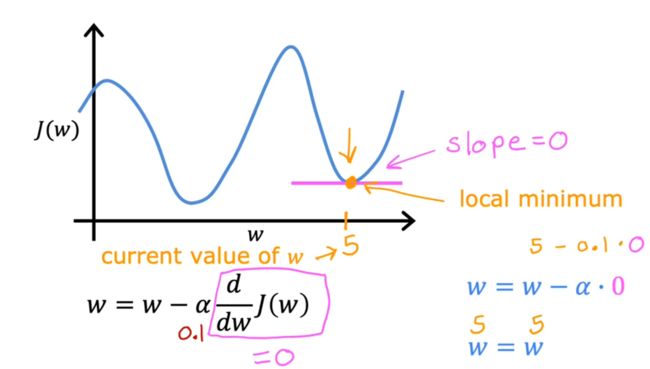
下面可以看到，选择合适的学习率可以达到局部最低点(local minimum)。

对于其他复杂的模型，可能有多个local minimum，这时不一定能确定此时的最小值就是全局的最小值global minimum。

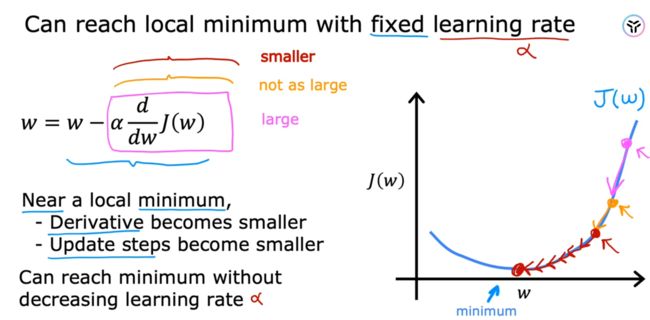
当接近极值点时，会发现有两个特性

• 导数项的值变小
• 每走一步的总步长变小

2.2.6：批量(batch)、时期(Epoch)

如下图，所谓batch，顾名思义，就是一批，" 一批完成一次梯度下降的所有训练样本"

• Batch（批，一批样本）：将整个样本分成若干个batch
• Batch_Size（批量大）：每批样本的样本个数
• Iteration（迭代）：一batch的样本完成一次梯度下降（反向传播），即为一次迭代
• Epoch（时期）：所有的样本完成一次训练（梯度下降/反向传播）。当一个Epoch中的样本数量过多时，就要分成多个batch。

ps：上面的"反向传播”是神经网络模型中的概念。

---

下期预告：多变量的线性回归模型、向量化、特征缩放、判断梯度是否收敛、如何设置合适的学习率、特征工程