数据结构-二叉树深度计算及平衡二叉树（AVL树）

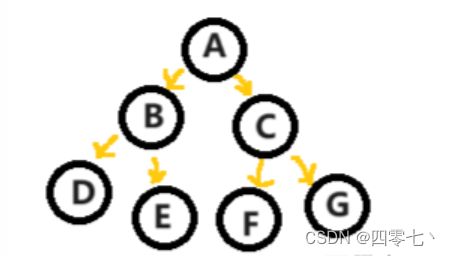
二叉树的深度指一棵树中结点到根结点的距离的最大值，一般令根结点为1，其子树深度为2，以此类推

计算二叉树的深度一般利用后序遍历法（左->右->根），先递归求出左右子树深度，再取最大值加1返回给双亲树，这样求出的其实是树的高度，但由于深度与高度数值相等，所以可以直接利用

即

int depth(BinaryTree* T){
	if (T==NULL) return 0;//如果为空，深度返回0
    int LeftD=depth(T->leftchild)+1;//加上这一层本身的深度
	int RightD=depth(T->rightchild)+1;
	return fmax(RightD,LeftD);//返回到这一层的最大深度
}

这棵树的运行结果：

为了提高树的搜索效率，二叉树应该尽量构建得趋于对称，如果出现一棵子树深度远高于另一颗的情况，极端一些如全将结点构建到右子树上，最终的树的效率会趋于线性结构

因此，我们要学会构建一棵趋于对称的二叉树。在二叉树的定义中，左右子树高度差不超过1的二叉树被称为平衡二叉树

（这样就是一棵非平衡二叉树）

由于自下向上返回高度，当一棵子树为非平衡二叉树时，它的双亲及祖先也不会是平衡二叉树，因此当一棵树不是avl树时，可以直接返回-1利于祖先树判断

即

int isbalanced(BinaryTree* T){
	if (T==NULL) return 0;
    int LeftD=isbalanced(T->leftchild);
	int RightD=isbalanced(T->rightchild);
	if(abs(LeftD-RightD)>1||RightD==-1||LeftD==-1) return -1;//判断子树或此树是否平衡
	else return fmax(RightD+1,LeftD+1);
}

再接收result，判断是否为-1，即可判断是否为avl树

int result=isbalanced(T);
	if (result!=-1) cout<<"Yes";

平衡二叉树的调整

将非平衡二叉树调整为平衡二叉树时，共四种情况

首先判断导致失衡的结点在根结点的哪一侧，接着判断在其双亲的哪一侧，都为左记为LL，左右记为LR，以此类推

LL型：取中间结点，将双亲作为自己的右孩子，如果自己有右孩子，则连接成双亲的左孩子

（即完成一次B为支点的右旋）

void LL(BinaryTree* T,BinaryTree** Root){//传入根结点和双亲结点
	BinaryTree* temp=T->leftchild;//temp记录失衡结点
	T->leftchild=temp->rightchild;//自己的右孩子成双亲的左孩子
	temp->rightchild=T;//双亲成为自己的右孩子
	*Root=temp;//失衡点成为新的根结点
}

RR型：取中间结点，使双亲成为自己的左孩子，如果自己有左孩子，则连接成双亲的右孩子

（完成一次C为支点的左旋）

void RR(BinaryTree* T,BinaryTree** Root){
	BinaryTree* temp=T->rightchild;//temp记录失衡结点
	T->rightchild=temp->leftchild;//自己的左孩子成双亲的右孩子
	temp->leftchild=T;//双亲成为自己的左孩子
	*Root=temp;//失衡点成为新的根结点
}}

LR型：取最后一个结点作为双亲，将双亲作为左孩子，双亲的双亲作为右孩子，原先的左孩子作为双亲的右孩子，右孩子作为双亲的双亲的左孩子。在此过程中，可以发现调整结果与进行一次RR调整，再进行一次LL调整是一样的

void LR(BinaryTree* T, BinaryTree** Root) {
    RR(T->leftchild, &T->leftchild);//子树左旋
    LL(T, Root);
}

RL型：取最后一个结点为双亲，原先的双亲作为自己的右孩子，双亲的双亲作为左孩子，自己的右孩子作为双亲的左孩子，左孩子作为双亲的双亲的右孩子（和上面反过来），同先LL调整再RR调整结果相同

void RL(BinaryTree* T,BinaryTree** Root){
	LL(T->rightchild,&T->rightchild)
	RR(T,Root);
}

（其实根据排序二叉树的性质，这些方法可以自己模拟推导一下，更易于理解）

这些树的调整都是从小到大调整的，因为子树平衡后双亲也更容易调整或也变为平衡，因此调整过程中提到的根结点是相对于调整的小树而言，而不是整体的大树