强化学习笔记
强化学习笔记 - 简介
本文是根据 Sutton的经典书籍 « Reinforcement Learning: An Introduction » 前三章内容整理的笔记。
【枯燥预警】本文侧重对强化学习概念的理论分析,在基本概念上的剖析较为详细,也就是说会比较无聊 LOL
1. 强化学习的概念
1.强化学习的概念
强化学习(reinforcement learning)研究的基本问题是,一个智能体(agent)与周围环境(environment)交互,每次交互都会获得来自环境的反馈或奖励(reward),从而不断修正自己的行为(action)来达到给定的目标。
其最重要的特征有两个,一是试错性搜索(trial-and-error search), 即智能体不会被告知该采取何种行为(action),而是自己去探索整个环境,并且有可能会做出错误的选择;二是延迟奖励(delayed reward),即智能体所采取的行动不仅会影响当前的奖励,还会作用到未来状态(state)的奖励。
2.强化学习和监督学习的区别
监督学习(supervised learning)是给定数据X和标签Y,学习X和Y之间的关系(映射);而强化学习没有给定的先验数据,是通过智能体不断试错来得到经验,不断学习并更新自己的经验来达到目的,这一点和人类的学习过程很类似。
3.强化学习的四个基本元素
在介绍具体的agent-environment框架之前,本文跟随Sutton课本的第一章,首先介绍强化学习的4个基本元素,即策略(policy),奖励函数(reward function),价值函数(value function) 和环境模型(model of environment).
3.1 策略
策略是指在给定的时刻,智能体与环境的交互方式。换句话说,策略就是在给定的状态下,智能体要采取何种行为。
3.2 奖励函数
奖励函数是整个强化学习问题最终的目标。比如围棋人工智能Alpha GO,它的目标是赢得一盘棋,那么如果赢了则奖励函数为1,输了奖励函数为-1。
3.3 价值函数
价值函数指从当前状态算起,未来一定数量的奖励函数的累加。如何计算/估计价值函数是整个强化学习的核心问题。
3.4 环境模型(可选)
用特定的模型来模拟环境。比如说,给定状态和行为的情况下,用模型可以预测下一个状态和奖励。环境模型不是必须的,有些强化学校问题是model-free的,即不需要特定的模型,只通过智能体与环境的交互和试错来完成学习。
4. 探索-利用问题
在强化学习中有一个很重要的概念,即探索-利用问题(exploration&exploitation trade-off). 一般来说,在做出行为(action)时,我们倾向于选择价值最大的那一个行为,这种选择被称为贪婪策略(greedy policy)。如果按照贪婪策略来选择行为,我们称之为利用(exploitation), 即利用现有的经验来做出选择;如果选择其他价值不是最高行为,我们称之为探索(exploration), 即探索其他行为可能带来的价值。Exploration & exploitation trade-off是强化学习的一个基本问题,因为exploitation可以在当前的时间节点做出价值最大的选择;然而可能有些选择在长期看来有更高的价值,但在当前时间节点却不是价值最高的,这时候就需要用exploration的策略去探索这些行为,来获得长期的最大收益。翻译成大白话就是,exploitation是选择当前利益最大的选项,考虑眼下的收益;而exploration是去尝试其他选项,考虑长远的收益。
一般在强化学习的开始阶段,使用较多exploration策略,充分探索整个假设空间;随着学习的进行,我们学习的策略(policy)越来越成熟,因而使用较多的exploitation策略,选择当下价值最大的行为[1]。
5. 智能体-环境交互模型:强化学习的基本框架
在1中我们提到了强化学习的基本问题是智能体与环境的交互,它是强化学习的基本框架,如图1所示。
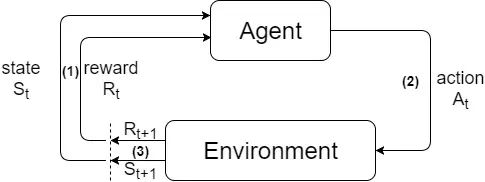
图1. 强化学习基本模型
在图1中,我们可以看到一个基本的强化学习步骤。在时刻t,第(1)步中智能体通过当前的状态St和奖励Rt,来决定要采取的行为。第(2)步中,智能体执行这个行为At,并在第(3)步中得到反馈,即t+1时刻的奖励Rt+1和新的状态St+1. 这样的一个过程称为一个阶段(episode)。强化学习的过程就是循环地执行每个episode,直到达到我们的学习目标。当t=0时,当前的状态S0和R0为事先设定好的初始值。下面,我们以图1中的框架为基础,定量地说明3中提到的两个基本要素:策略和奖励。
5.1 策略(π)
策略π指在当前状态下,选择每个动作的概率。即
π t ( a ∣ s ) = P ( A t = a ∣ S t = s ) ( 1 ) \pi_{t}(a|s)=P(A_{t}=a|S_{t}=s)\:\:\:(1) πt(a∣s)=P(At=a∣St=s)(1)
5.2奖励(Reward)与回报(Return)
奖励代表着强化学习的最终目标。我们要奖励(或惩罚)的是最终我们是否达到了我们的目的,而不是我们实现目的的方式。这里有点拗口,举个例子:在象棋AI的训练中,我们的奖励函数应当是我们最终是否赢得了比赛,如果赢了奖励为1,输了奖励为-1. 但是下棋中的走法,比如吃了对方一个子,或者将了对方一军,都不应该被算作奖励的对象。因为我们只关注最终的胜负,至于如何赢,就交给智能体自己去学习,我们不要把自己的经验强加给他。这是强化学习试错机制的体现(即不给任何先验知识),也是为什么AI可以打败人类顶尖棋手的原因之一。
奖励是执行当前动作获得的即使回报,而我们追求的应当是长期累积奖励,即回报(return). 回报有两种定义方式:
形式1
考虑最简单的情况,回报Gt定义为从当前时间点开始,一定时间内奖励Rt的累加:
G t = R t + 1 + R t + 2 + . . . + R T ( 2 ) G_{t}=R_{t+1}+R_{t+2}+...+R_{T}\:\:\:(2) Gt=Rt+1+Rt+2+...+RT(2)
这种定义方式适用于片段式任务(Episodic Task), 即强化学习任务可以被分解为有限个时间节点,或有限个episodes,经过一定时间的学习后任务会达到最终状态(Terminal State)并自然结束。
形式2
现实中有些任务并没有明确的最终状态,而是会一直延续下去,我们把这种称之为持续性任务(Continuing Task),即 T = ∞. 此时(1)中的回报定义方式是发散的,因此需要引入衰减(Discounting)的概念。我们定义把回报定义为衰减的奖励函数的累积:
G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 . . . + ∞ ( 3 ) G_{t}=R_{t+1}+\gamma R_{t+2}+\gamma^{2}R_{t+3}...+\infty\:\:\:(3) Gt=Rt+1+γRt+2+γ2Rt+3...+∞(3)
其中γ为衰减率,0 ≤ γ ≤ 1.
6. 马尔科夫决策过程
6.1 马尔科夫性质(Markov Property):
系统的下个状态只与当前的状态信息有关,而与更早的状态无关。
6.2 马尔科夫决策过程(Markov Decision Process, MDP)
马尔科夫决策过程即满足马尔科夫性质的强化学习问题。如果该MDP的状态数目是有限的,则称为有限马尔科夫决策过程(finite MDP).
可以用转移概率(transition probabilities)来定义一个有限MDP
p ( s ′ ∣ s , a ) = P r { S t + 1