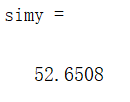神经网络入门必备——BP神经网络
神经网络入门必备——BP神经网络
文章目录
- 神经网络入门必备——BP神经网络
-
- 一、什么是BP神经网络
- 二、BP神经网络的工作原理
-
- 2.1 BP神经网络的逻辑模型
- 2.2 BP神经网络的权重迭代原理
- 三、BP神经网络训练示例
- 四、BP神经网络的缺点
一、什么是BP神经网络
神经网络是模仿人的神经元处理方式而诞生的数学模型,BP神经网络是神经网络中最经典的一个,也是最早被广泛应用的一种神经网络模型之一。
BP神经网络由多个神经元组成,神经元之间通过连接权重进行连接。每个神经元接收输入信号并通过激活函数进行处理,然后将输出传递给下一个神经元。BP神经网络的名字来源于其训练算法,即反向传播算法,该算法是一种用于调整神经网络连接权重的方法。
二、BP神经网络的工作原理
2.1 BP神经网络的逻辑模型
符号说明:
| 符号 | 说明 |
|---|---|
| X i X_i Xi | 输入数据 |
| W i j W_{ij} Wij | 权重 |
| β i \beta_i βi | 偏置 |
BP神经网络分为输入层、隐藏层和输出层。以下图为例,由输入层输入数据,向隐藏层传输一个带有权重(W)的数据。由此原理可知,下一层的“神经元”收到的数据是 X i ∗ W i X_i*W_i Xi∗Wi。
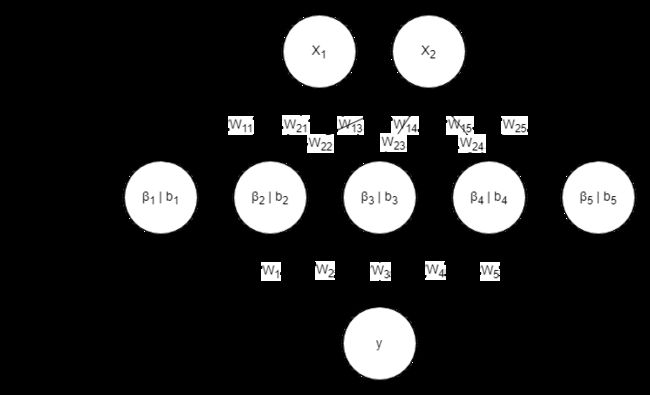
一般激活函数为 l o g s i g logsig logsig,其表达式为:
f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1
所以在隐藏层中,收到上一层的数据,处理方式为
l o g s i g ( X i W i j + X i + 1 W i j + 1 + β i ) logsig(X_iW_{ij}+X_{i+1}W_{ij+1}+\beta_i) logsig(XiWij+Xi+1Wij+1+βi)
则上表视图中 y y y的表达式为: y = ∑ m = 0 m < 5 l o g s i g ( W m ∑ i = 0 i < 2 ∑ j = 0 j < 5 W i j X i + β j + β y ) y=\sum_{m=0}^{m<5}logsig(W_m \sum_{i=0}^{i<2}\sum_{j=0}^{j<5}W_{ij}X_i+\beta_j+\beta_y) y=m=0∑m<5logsig(Wmi=0∑i<2j=0∑j<5WijXi+βj+βy)
2.2 BP神经网络的权重迭代原理
符号说明:
| 符号 | 说明 |
|---|---|
| m m m | 训练样本个数 |
| k k k | 输出个数 |
| y ^ i j \hat y_{ij} y^ij | 第i个样本第k个输出的预测值 |
| y i j y_{ij} yij | 第i个样本第k个输出的真实值 |
| b b b | 权重阈值 |
BP神经网络采用的梯度下调权重的方式,经过数据处理后,对数据进行均方误差函数计算,公式如下:
E ( W , b ) = 1 m ∑ i = 1 m 1 k ∑ j = 1 k ( y ^ i j − y i j ) 2 E(W,b)=\frac{1}{m} \sum_{i=1}^{m}\frac{1}{k} \sum_{j=1}^{k}(\hat{y}_{ij}-y_{ij})^2 E(W,b)=m1i=1∑mk1j=1∑k(y^ij−yij)2
数据通过均方误差计算,得到符合期望的值后输出得到合适的值,并得到 W W W和 b b b值

三、BP神经网络训练示例
这是一个模拟的数据,以工作、家庭、娱乐三个方面得出幸福度。

在MATLAB中,将工作、家庭、娱乐三项作为输入数据,幸福度作为输出数据进行模型训练。
x1=[50,40,80,70];
x2=[30,20,40,40];
x3=[60,50,20,40];
y=[40,35,60,63];
input=[x1;x2;x3];
output=y;
setdemorandstream(88888);
net = newff(input,output,5,{'logsig','purelin'},'trainlm');%%神经元5个
net.trainparam.goal = 0.0001; %%均方误差目标
net.trainparam.show = 400; %%每400次展示一次
net.trainparam.epochs = 15000; %%训练15000次
[net,tr] = train(net,input,output);
simout = sim(net,input);
figure;
t=1:length(simout);
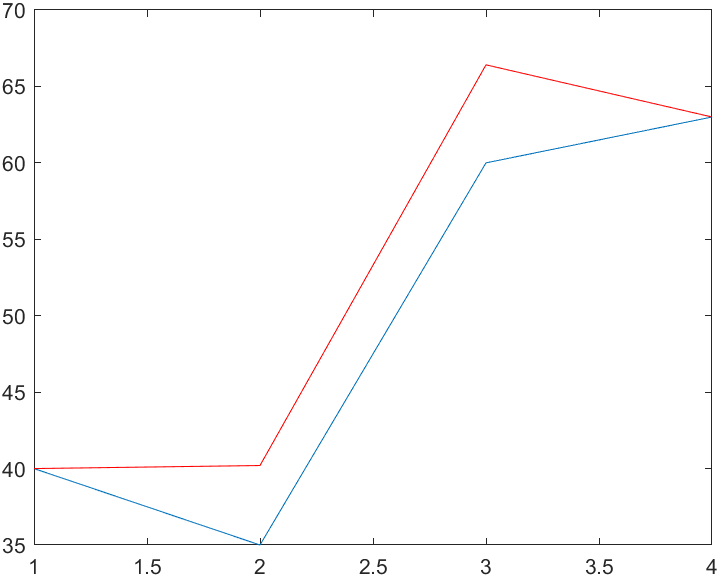
plot(t,y,t,simout,'r')
训练完成后,会得出一个对比图(蓝色为原始图像,红色为预测图像)
得到训练模型后,写入代码或者在命令框内输入
x=[30;60;50];
simy = sim(net,x)
四、BP神经网络的缺点
1、训练时间长:BP神经网络的训练过程需要大量的迭代计算,因此训练时间较长;
2、由于BP神经网络采用梯度下降算法来优化网络权重,存在着陷入局部最小值的问题;
3、BP神经网络对输入数据的变化非常敏感。