【翻译】GPT-3架构，简述于“餐巾纸”上

这是一篇技术派文章，尤其是其中的绘制于“餐巾纸”上的手绘图，从数学角度对于大语言模型的架构给你一些新的启发。

原文链接：https://dugas.ch/artificial_curiosity/GPT_architecture.html
作者：Daniel Dugas
翻译/编辑：liyane 使用LLM Chat API翻译；为了方便对照，把英文原文也对应在每段中文翻译之下。

现在马上跟随作者开始一次开心的旅程：

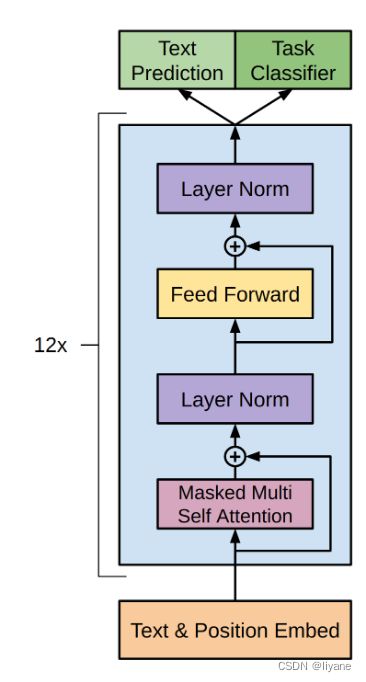
GPT-3架构，简述于“餐巾纸”上

有太多关于GPT-3的精彩文章，展示了它能做什么，思考其后果，可视化其工作原理。即使有这些，我仍需要查阅多篇论文和博客，才确信我已经理解了架构。

因此，此页面的目标很简单：帮助其他人尽可能详细地理解GPT-3架构。

如果你没有耐心看完过程和细节，直接跳到完整架构草图。

The GPT-3 Architecture, on a Napkin

There are so many brilliant posts on GPT-3, demonstrating what it can do, pondering its consequences, vizualizing how it works. With all these out there, it still took a crawl through several papers and blogs before I was confident that I had grasped the architecture.
So the goal for this page is humble, but simple: help others build an as detailed as possible understanding of the GPT-3 architecture.
Or if you’re impatient, jump straight to the full-architecture sketch.

原始图表

作为起点，原始的transformer和GPT论文[^1][2][^3]为我们提供了以下图表：

就图表而言，不错，但如果你像我一样，这些还不足以理解全部画面。那么，让我们深入了解！

Original Diagrams

As a starting point, the original transformer and GPT papers[1][2][3] provide us with the following diagrams:

Not bad as far as diagrams go, but if you’re like me, not enough to understand the full picture. So let’s dig in!

输入/输出

在我们能理解任何其他事情之前，我们需要知道：GPT的输入和输出是什么？

输入是N个单词（也称为标记）的序列。 输出是一个猜测，猜测最有可能被放在输入序列末尾的单词。

就是这样！你看到的所有令人印象深刻的GPT对话、故事和示例都是用这个简单的输入输出方案制作的：给它一个输入序列 - 获得下一个单词。

Not all heroes wear-> capes

当然，我们通常想要获得不止一个单词，但那不是问题：获取下一个单词后，我们将其添加到序列中，并获取下一个单词。

Not all heroes wear capes -> but
Not all heroes wear capes but -> all
Not all heroes wear capes but all -> villans
Not all heroes wear capes but all villans -> do

根据需要重复此过程，你最终会得到长篇生成的文本。

实际上，为了准确，我们需要在两个方面纠正上述内容。

1. 输入序列实际上固定为2048个单词（对于GPT-3）。我们仍然可以传入短序列作为输入：我们简单地用“空”值填充所有额外的位置。

2. GPT的输出不仅仅是一个猜测，而是一个序列（长度2048）的猜测（每个可能的单词一个概率）。序列中的每个’下一个’位置都有一个。但在生成文本时，我们通常只看序列的最后一个单词的猜测。
   

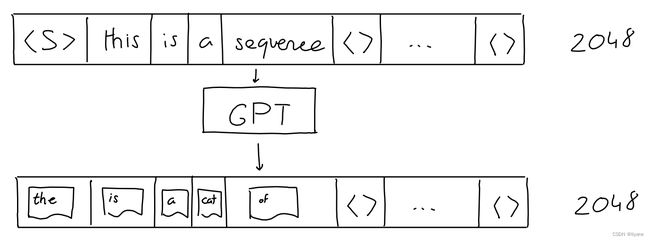
就是这样！序列进，序列出。

In / Out

Before we can understand anything else, we need to know: what are the inputs and outputs of GPT?

The input is a sequence of N words (a.k.a tokens). The output is a guess for the word most likely to be put at the end of the input sequence.

That’s it! All the impressive GPT dialogues, stories and examples you see posted around are made with this simple input-output scheme: give it an input sequence – get the next word.

Not all heroes wear -> capes

Of course, we often want to get more than one word, but that’s not a problem: after we get the next word, we add it to the sequence, and get the following word.

Not all heroes wear capes -> but
Not all heroes wear capes but -> all
Not all heroes wear capes but all -> villans
Not all heroes wear capes but all villans -> do

repeat as much as desired, and you end up with long generated texts.

Actually, to be precise, we need to correct the above in two aspects.

1. The input sequence is actually fixed to 2048 words (for GPT-3). We can still pass short sequences as input: we simply fill all extra positions with “empty” values.
2. The GPT output is not just a single guess, it’s a sequence (length 2048) of guesses (a probability for each likely word). One for each ‘next’ position in the sequence. But when generating text, we typically only look at the guess for the last word of the sequence.

That’s it! Sequence in, sequence out.

编码

但是等一下，GPT实际上并不理解单词。作为一个机器学习算法，它操作的是数字向量。那么我们如何将单词转换为向量呢？

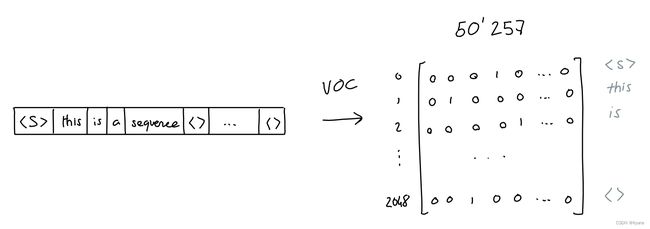
第一步是保留所有单词的词汇表，这允许我们给每个单词一个值。Aardvark为0，aaron为1，依此类推。 （GPT拥有50257个单词的词汇表）。

结果，我们可以将每个单词转换成一个大小为50257的一位热编码（one-hot encoding）向量，其中只有索引i（单词的值）处的维度为1，所有其他维度都为0。

当然，我们对序列中的每个单词都这样做，这会产生一个2048 x 50257的由一和零组成的矩阵。

注意：为了效率，GPT-3实际上使用字节级Byte Pair Encoding（BPE）分词。这意味着词汇表中的“单词”不是完整的单词，而是文本中经常出现的字符组（对于字节级BPE，是字节）。使用GPT-3字节级BPE分词器，“Not all heroes wear capes”被分割为标记"Not" “all” “heroes” “wear” “cap” “es”，在词汇表中的id分别为3673, 477, 10281, 5806, 1451, 274。这里有一个很好的介绍该主题的文章，以及一个github实现，你可以自己尝试。

2022年编辑：OpenAI现在有一个分词器工具，允许你输入一些文本并查看它是如何被分解为标记的。

Encoding

But wait a second, GPT can’t actually understand words. Being a machine-learning algorithm, it operates on vectors of numbers. So how do we turn words into vectors?

The first step is to keep a vocabulary of all words, which allows us to give each word a value. Aardvark is 0, aaron is 1, and so on. (GPT has a vocabulary of 50257 words).

As a result, we can turn each word into a one-hot encoding vector of size 50257, where only the dimension at index i (the word’s value) is 1, and all others are 0.

Of course, we do this for every word in the sequence,
Which results in a 2048 x 50257 matrix of ones and zeroes.

Note: For efficiency, GPT-3 actually uses byte-level Byte Pair Encoding (BPE) tokenization. What this means is that “words” in the vocabulary are not full words, but groups of characters (for byte-level BPE, bytes) which occur often in text.
Using the GPT-3 Byte-level BPE tokenizer, “Not all heroes wear capes” is split into tokens “Not” “all” “heroes” “wear” “cap” “es”, which have ids 3673, 477, 10281, 5806, 1451, 274 in the vocabulary.
Here is a very good introduction to the subject, and a github implementation so you can try it yourself.

2022 edit: OpenAI now has a tokenizer tool, which allows you to type some text and see how it gets broken down into tokens.

嵌入

50257对于一个向量来说相当大，并且它主要是由零填充的。这浪费了很多空间。

为了解决这个问题，我们学习了一个嵌入函数：一个神经网络，它接收一个长度为50257的由一和零组成的向量，并输出一个长度为n的数字向量。在这里，我们试图将单词的含义的信息存储（或投影）到一个更小的维度空间中。

例如，如果嵌入维度是2，就像在2D空间中的特定坐标存储每个单词一样。

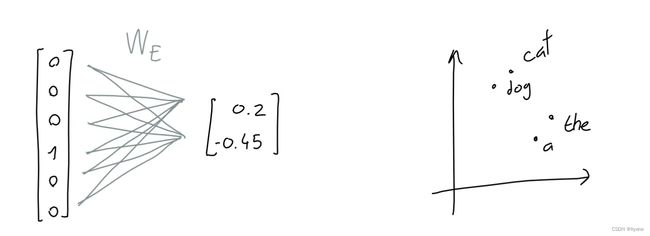
另一个直观的思考方式是，每个维度是一个虚构的属性，比如“软度”，或“shmlorbness”，并且给定每个属性的一个值，我们就可以准确知道哪个单词被指代。

当然，嵌入维度通常大于2：GPT使用12288维。

实际上，每个单词的一位热向量与学习到的嵌入网络权重相乘，最终成为一个12288维的嵌入向量。

在算术术语中，我们将2048 x 50257的序列编码矩阵与50257 x 12288的嵌入权重矩阵（学习得到的）相乘，最终得到一个2048 x 12288的序列嵌入矩阵。

从现在开始，我会将2D矩阵绘制为小小的块，旁边写着它们的维度。如适用，我分隔矩阵线条以清楚地表明，每行对应序列中的一个单词。

另外请注意，由于矩阵乘法的工作方式，嵌入函数（即嵌入权重矩阵）被分别应用于每个单词编码（即序列编码矩阵中的行）。换句话说，结果与将每个单词编码向量分别传递给嵌入函数并在最后将所有结果拼接起来相同。这意味着：在此过程中，序列中没有信息流动，也没有关于标记的绝对或相对位置的信息。

Embedding

50257 is pretty big for a vector, and it’s mostly filled with zeroes. That’s a lot of wasted space.

To solve this, we learn an embedding function: a neural network that takes a 50257-length vector of ones and zeroes, and outputs a n-length vector of numbers. Here, we are trying to store (or project) the information of the word’s meaning to a smaller dimensional space.

For example, if the embedding dimension is 2, it would be like storing each word at a particular coordinate in 2D space.

Another intuitive way to think about it is that each dimension is a made-up property, like “softness”, or “shmlorbness”, and given a value for each property we can know exactly which word is meant.

Of course, the embedding dimensions are typically larger than 2: GPT uses 12288 dimensions.

In practice, each word one-hot vector gets multiplied with the learned embedding network weights, and ends up as a 12288 dimension embedding vector.

In arithmetic terms, we multiply the 2048 x 50257 sequence-encodings matrix with the 50257 x 12288 embedding-weights matrix (learned) and end up with a 2048 x 12288 sequence-embeddings matrix.

From now on, I will draw 2D matrices as small little blocks with the dimensions written next to them.
When applicable, I separate the matrix lines to make it clear that each line corresponds to a word in the sequence.

Also note that due to how matrix multiplication works, the embedding function (a.k.a the embedding weight matrix) is applied to each word encoding (a.k.a row in the sequence-encodings matrix) separately. In other words, the result is the same as passing each word encoding vector separately to the embedding function, and concatenating all the results at the end. What this means: this far in the process, there is no information flowing across the sequence, and no information on the absolute or relative position of tokens.

位置编码

为了编码当前标记在序列中的位置，作者取标记的位置（一个标量i，范围[0-2047]）并通过12288个正弦函数，每个具有不同的频率，进行传递。

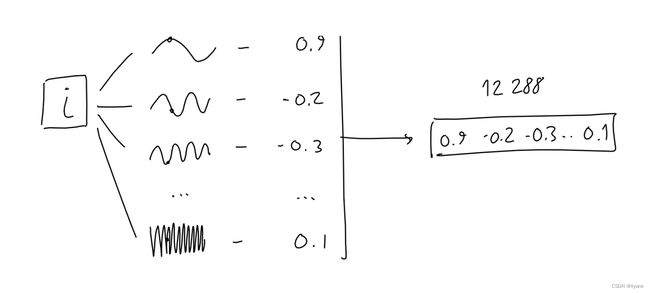
为什么这样做有效的确切原因对我来说并不完全清楚。作者将其解释为产生了许多相对位置编码，这对模型很有用。为了分析此选择的其他可能心智模型：考虑信号经常被表示为周期样本之和（参见傅立叶变换或SIREN网络架构），或者语言自然呈现出各种长度的周期（例如，诗歌）。

结果是，每个标记都是一个12288维的数字向量。就像嵌入一样，我们将这些向量组合成一个具有2048行的单独矩阵，其中每行是序列中一个标记的12288列位置编码。

最终，这个序列位置编码矩阵，形状与序列嵌入矩阵相同，可以简单地加到它上面。

Positional Encoding

To encode the position of the current token in the sequence, the authors take the token’s position (a scalar i, in [0-2047]) and pass it through 12288 sinusoidal functions, each with a different frequency.

The exact reason for why this works is not entirely clear to me. The authors explain it as yielding many relative-position encodings, which is useful for the model. For other possible mental models to analyze this choice: consider the way signals are often represented as sums of periodic samples (see fourier transforms, or SIREN network architecture), or the possibility that language naturally presents cycles of various lengths (for example, poetry).

The result is, for each token, a 12288 vector of numbers. Just as with the embeddings, we combine those vectors into a single matrix with 2048 rows, where each row is the 12288-column positional-encoding of a token in the sequence.

Finally, this sequence-positional-encodings matrix, having the same shape as the sequence-embeddings matrix, can simply be added to it.

注意（简化版本）

简单地说，注意机制的目的是：对于序列中的每个输出，预测要关注哪些输入标记以及关注的程度。这里，想象一个由3个标记组成的序列，每个都用512值的嵌入表示。

模型学习了3个线性投影，它们都应用于序列嵌入。换句话说，学习了3个权重矩阵，将我们的序列嵌入转换为三个不同任务的三个独立的3x64矩阵。

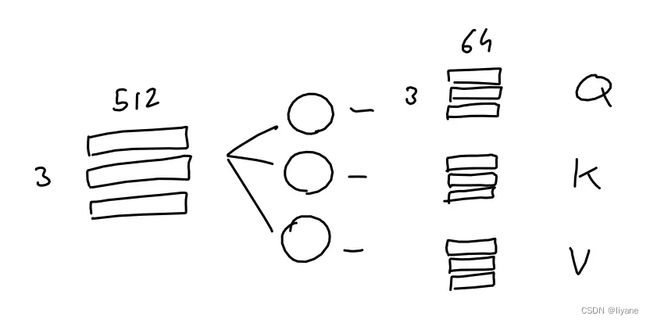
前两个矩阵（“查询”和“键”）相乘（QK^T），产生一个3x3矩阵。这个矩阵（通过softmax标准化）表示每个标记对其他标记的重要性。

注意：这个（QK^T）是GPT中唯一在序列中的词之间进行操作的操作。它是唯一一个矩阵行相互作用的操作。

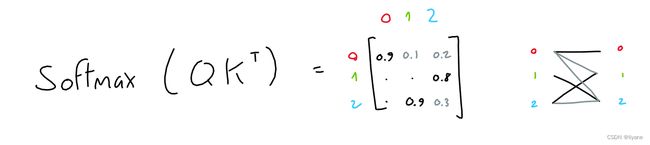
第三个矩阵（“值”）与这个重要性矩阵相乘，从而产生每个标记的所有其他标记值的混合，这些标记的值根据各自标记的重要性加权。

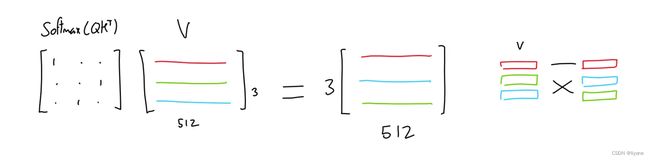
例如，如果重要性矩阵仅包含一和零（每个标记只有一个其他标记很重要），结果类似于根据哪个标记最重要来选择值矩阵中的行。

我希望这有助于理解注意机制的直观过程，或者至少帮助理解所使用的确切代数。

Attention (Simplified)

Simply put, the purpose of attention is: for each output in the sequence, predict which input tokens to focus on and how much. Here, imagine a sequence of 3 tokens, each represented with a 512-values embedding.

The model learns 3 linear projections, all of which are applied to the sequence embeddings. In other words, 3 weight matrices are learned which transform our sequence embeddings into three separate 3x64 matrices, each purposed for a different task.

The first two matrices (“queries” and “keys”) are multiplied together (QK^T), which yields a 3x3 matrix.This matrix (normalized through softmax) represents the importance of each token to each other tokens.

Note: This (QK^T) is the only operation in GPT which operates across words in the sequence. It is the only operation where matrix rows interact.

The third matrix (“values”) is multiplied with this importance matrix, resulting in, for each token, a mix of all other token values weighted by the importance of their respective tokens.

For example, if the importance matrix is only ones and zeroes (each token has only one other token which is of importance), the result is like selecting rows in the values matrix based on which token is most important.

I hope that this helped, if not with the intuitive understanding of the attention process, at least with understanding the exact algebra which is used.

多头注意

现在，在作者介绍的GPT模型中，他们使用了多头注意。这意味着上述过程被多次重复（在GPT-3中是96次），每次都使用不同的学习到的查询、键、值投影权重。

每个注意头的结果（单个2048 x 128矩阵）被连在一起，产生一个2048 x 12288的矩阵，然后再以线性投影（不改变矩阵形状）乘以它，以求稳妥。

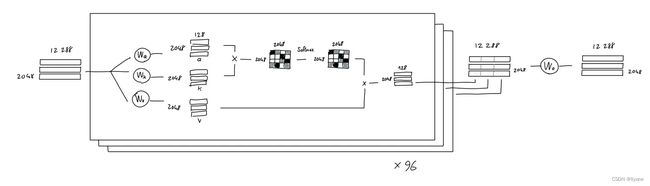
注意：论文提到GPT-3使用稀疏注意，这允许更有效的计算。老实说，我还没有花时间去完全理解它是如何实现的。祝你好运！

“吹毛求疵”：上述图示意味着每个注意头有单独的权重矩阵。然而，实际上，注意模型实现可能使用一个大的组合权重张量来完成所有头的矩阵乘法，然后将其分割为每个头的a、k、v矩阵。不用担心：从理论上讲，这也不应该影响模型输出，因为代数运算是相同的。（感谢Kamilė Lukošiūtė提出这一点）

Multi-Head Attention

Now, in the GPT model presented by the authors, they use multi-head attention. All this means is that the above process is repeated many times (96x in GPT-3), each with a different learned query, key, value projection weights.

The result of each attention head (a single 2048 x 128 matrix) are concatenated together, yielding a 2048 x 12288 matrix, which is then multiplied with a linear projection (which doesn’t change the matrix shape), for good measure.

Note: the paper mentions that GPT-3 uses sparse attention, which allows more efficient computation.
Honestly, I haven’t taken the time to understand exactly how it’s implemented. You’re on your own, good luck!

‘Splitting hairs’: The above drawing implies separate weights matrices for each head. However, in practice, attention models implementations may use a single big combined weight tensor for all the heads, do the matrix multiplication once, and then split it into each head’s a, k, v matrices. Not to worry: In theory, it should also not affect model outputs, since the algebraic operations are the same. (thanks to Kamilė Lukošiūtė for raising this point)

前馈

前馈块是一个拥有1个隐藏层的好老式多层感知器。取输入，乘以学习到的权重，加上学习到的偏置，重复一遍，得到结果。

这里，输入和输出形状相同（2048 x 12288），但隐藏层的大小是4*12288。

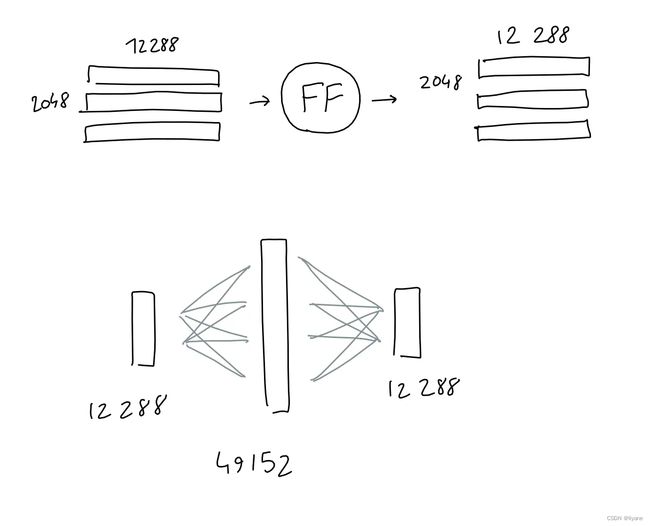
为了清楚：我也将这个操作绘制为一个圆圈，但与架构中的其他学习投影（嵌入、查询/键/值投影）不同，这个“圆圈”实际上由两个投影（将输入与学习到的权重矩阵相乘）连续组成，每次都在之后加上学习到的偏置，并最终应用ReLU激活函数。

Feed Forward

The feed forward block is a good-old multi-layer-perceptron with 1 hidden layer. Take input, multiply with learned weights, add learned bias, do it again, get result.

Here, both input and output shapes are the same ( 2048 x 12288 ), but the hidden layer has a size 4*12288.

To be clear: I also draw this operation as a circle, but unlike other learned projections in the architecture (embedding, query/key/value projections) this “circle” actually consists of two projections (learned-weight matrix multiplied with the input) in a row, with the learned biases added after each one, and finally a ReLU.

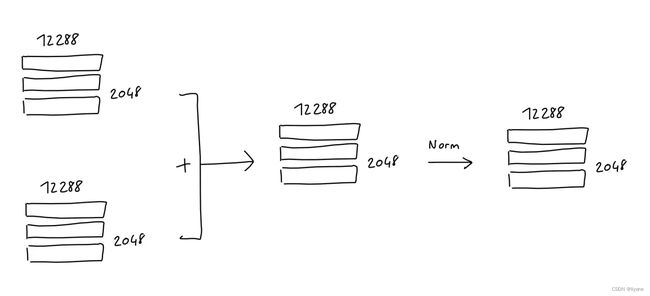
加法 & 归一化

在多头注意力机制和前馈块之后，会将块的输入加到它的输出上，然后对结果进行归一化处理。
这在深度学习模型中很常见（自ResNet以来）。

注意：我的任何草图中都没有反映出自GPT-2以来的一个事实，“层归一化被移至每个子块的输入处，类似于预激活残差网络，并且在最后一个自注意力块之后增加了一个额外的层归一化”

Add & Norm

After both the Multi-Head attention and the Feed Forward blocks, the input of the block is added to it’s output, and the result is normalized. This is common in deep learning models (since ResNet).

Note: Not reflected in any of my sketches is the fact that since GPT-2, “Layer normalization was moved to the input of each sub-block, similar to a pre-activation residual network and an additional layer normalization was added after the final self-attention block”

解码

我们快到了！经过GPT-3的全部96层注意力/神经网络机制处理后，输入被处理成一个2048 x 12288的矩阵。这个矩阵应该包含序列中每个2048输出位置的一个12288向量，这个向量包含了应该出现的单词的信息。但我们如何提取这些信息呢？

如果你还记得嵌入部分，我们学习了一个映射，它可以将一个给定的（单词的独热编码）转化成一个12288向量嵌入。结果表明，我们可以简单地反转这个映射，将我们的输出12288向量嵌入转换回50257单词编码。想法是，如果我们花了这么大的精力学习从单词到数字的良好映射，我们不妨重用它！

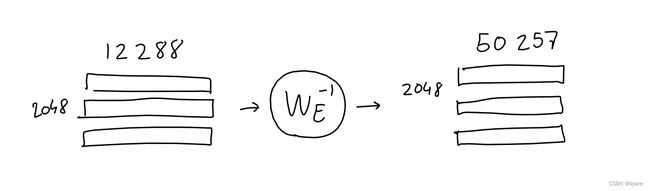
当然，这样做不会像我们开始时那样给我们0和1，但这是好事：经过一个快速的softmax后，我们可以将结果值视为每个单词的概率。

另外，GPT论文提到了参数top-k，它限制了在输出中可能采样的单词数量，仅限于k个最可能预测的单词。例如，当top-k参数为1时，我们总是选择最可能的单词。

Decoding

We’re almost there! Having passed through all 96 layers of GPT-3’s attention/neural net machinery, the input has been processed into a 2048 x 12288 matrix. This matrix is supposed to contain, for each of the 2048 output positions in the sequence, a 12288-vector of information about which word should appear. But how do we extract this information?

If you remember in the Embedding section, we learned a mapping which transforms a given (one-hot encoding of a) word, into a 12288-vector embedding. It turns out, we can just reverse this mapping to transform our output 12288-vector embedding back into a 50257-word-encoding. The idea is, if we spent all this energy learning a good mapping from word to numbers, we might as well reuse it!

Of course, doing this won’t give us ones and zeroes like we started with, but that’s a good thing: after a quick softmax, we can treat the resulting values as probabilities for each word.

In addition, the GPT papers mention the parameter top-k, which limits the amount of possible words to sample in the output to the k most likely predicted words. For example, with a top-k parameter of 1, we always pick the most likely word.

完整架构

就这样：一些矩阵乘法，一些代数运算，我们就得到了一个最先进的自然语言处理巨头。我把所有部分绘制成一个单独的示意图，请点击查看完整尺寸版本。

包含可学习权重的操作用红色高亮显示 。

Full Architecture

And there you have it: a few matrix multiplications, some algebra, and we have ourselves a state-of-the-art, natural language processing monster. I’ve drawn all of the parts together into a single schematic, click it to see the full-sized version.
The operations which contain learnable weights are highlighted in red.

参考文献

[^1] Radford, A., Narasimhan, K., Salimans, T. 和 Sutskever, I., 2018. 通过生成式预训练提升语言理解。
[^2] Radford, A., Wu, J., Child, R., Luan, D., Amodei, D. 和 Sutskever, I., 2019. 语言模型是无监督的多任务学习者。OpenAI博客, 1(8), 第9页。
[^3] Brown, T., Mann, B., Ryder, N., Subbiah, M., Kaplan, J.D., Dhariwal, P., Neelakantan, A., Shyam, P., Sastry, G., Askell, A. 和 Agarwal, S., 2020. 语言模型是小样本学习者。神经信息处理系统进展, 33, 页1877-1901

References

[^1] Radford, A., Narasimhan, K., Salimans, T. and Sutskever, I., 2018. Improving language understanding by generative pre-training.
[^2] Radford, A., Wu, J., Child, R., Luan, D., Amodei, D. and Sutskever, I., 2019. Language models are unsupervised multitask learners. OpenAI blog, 1(8), p.9.
[^3] Brown, T., Mann, B., Ryder, N., Subbiah, M., Kaplan, J.D., Dhariwal, P., Neelakantan, A., Shyam, P., Sastry, G., Askell, A. and Agarwal, S., 2020. Language models are few-shot learners. Advances in neural information processing systems, 33, pp.1877-1901