路径跟踪算法Stanley 实现 c++
参考博客:【自动驾驶】Stanley(前轮反馈)实现轨迹跟踪 | python实现 | c++实现
Stanley
前轮反馈控制(Front wheel feedback),又称Stanley控制。
核心思想:基于前轮中心的路径跟踪偏差量对方向盘转向控制量进行计算(Pure Pursuit是基于后轮中心)。
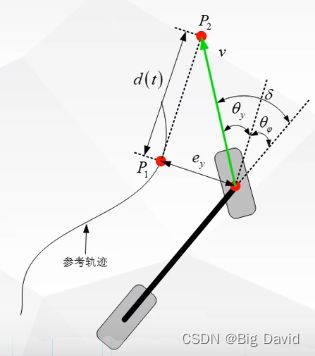
前轮转角控制量:
δ = θ φ + θ y \large\delta =\theta _{\varphi }+\theta _{y } δ=θφ+θy
- 由航向误差引起的转角 θ φ \theta _{\varphi } θφ,即当前车身方向与参考轨迹最近的点 P 1 P_{1} P1的切线方向的夹角。
- 由横向误差引起的转角 θ y \theta _{y } θy,即前轮中心到参考轨迹最近点 P 1 P_{1} P1的横向距离 e y e_{y} ey
δ = θ φ + θ y = θ φ + a r c t a n e y d \large\delta =\theta _{\varphi }+\theta _{y }=\theta _{\varphi }+arctan\frac{e_{y}}{d} δ=θφ+θy=θφ+arctandey
横向误差变化率: e y ˙ = − v s i n θ y ≈ − v θ y ≈ − v t a n θ y = − v e y d \dot{e_{y}} =-vsin\theta _{y }\approx -v\theta _{y }\approx -vtan\theta _{y }=-v\frac{e_{y}}{d} ey˙=−vsinθy≈−vθy≈−vtanθy=−vdey
e y ˙ ≈ − v d e y \dot{e_{y}} \approx-\frac{v}{d}e_{y} ey˙≈−dvey得:
e ( t ) = e ( 0 ) e − k t = e ( 0 ) e − v d t e(t)=e(0)e^{-kt }=e(0)e^{-\frac{v}{d}t } e(t)=e(0)e−kt=e(0)e−dvt
1 Stanley控制器设计如下:
δ ( k ) = θ e ( k ) + a r c t a n k e ( k ) v ( k ) \large\delta(k)=\theta _{e}(k)+arctan\frac{ke(k)}{v(k)} δ(k)=θe(k)+arctanv(k)ke(k)
其中, θ e ( k ) \theta _{e}(k) θe(k)为k时刻的航向角偏差,e(k)为横向跟踪误差,k为需要调节的参数,v为无人车当前速度。
输入:当前车辆位置、航向角 ψ ψ ψ、速度 v v v、当前目标路点和离车辆前轴中心最近目标路径点的航向角 ψ t ψ_t ψt
计算横向误差 e y e_y ey
计算 δ = ψ t − ψ + a r c t a n k e y v δ=ψ_t−ψ+arctan\frac{ke_y}{v} δ=ψt−ψ+arctanvkey
输出:前轮转角控制量 δ \delta δ
2 Stanley控制器代码
stanley.h
#pragma once
#include stanley.cpp
#include "Stanley.h"
Stanley::Stanley(double k)
{
this->k = k;
}
// 搜索目标邻近路点
// robot_state 当前机器人位置 ref_path 参考轨迹(数组)
double Stanley::calTargetIndex(vector<double> robot_state, vector<vector<double>> ref_path)
{
vector<double> dists;
for (vector<double> xy : ref_path)
{
double dist = sqrt(pow(xy[0] - robot_state[0], 2) + pow(xy[1] - robot_state[1], 2));
dists.push_back(dist);
}
return min_element(dists.begin(), dists.end()) - dists.begin();
}
// 角度归一化到[-PI, PI]
double Stanley::normalizeAngle(double angle)
{
while (angle > PI)
{
angle -= 2.0 * PI;
}
while (angle < -PI)
{
angle += 2.0 * PI;
}
return angle;
}
// stanley 控制
// robot_state:x,y,yaw,v ref_path:x,y,theta
// return 控制量 + 目标点索引
vector<double> Stanley::stanleyControl(vector<double> robot_state, vector<vector<double>> ref_path)
{
double current_target_index = calTargetIndex(robot_state, ref_path);
vector<double> current_ref_point;
if (current_target_index >= ref_path.size())
{
current_target_index = ref_path.size() - 1;
current_ref_point = ref_path[ref_path.size() - 1];
} else {
current_ref_point = ref_path[current_target_index];
}
double e_y;
double psi_t = current_ref_point[2];
if ((robot_state[0] - current_ref_point[0]) * psi_t - (robot_state[1] - current_ref_point[1]) > 0)
{
e_y = sqrt(pow(current_ref_point[0]-robot_state[0],2)+pow(current_ref_point[1]-robot_state[1],2));
}
else
{
e_y = -sqrt(pow(current_ref_point[0]-robot_state[0],2)+pow(current_ref_point[1]-robot_state[1],2));
}
double psi = robot_state[2];
double v = robot_state[3];
double theta_e = psi_t - psi;
double delta_e = atan2(k * e_y, v);
double delta = normalizeAngle(delta_e + theta_e);
return {delta, current_target_index};
}
main.cpp
#include "Stanley.h"
#include "matplotlibcpp.h"
#include "KinematicModel.h"
namespace plt = matplotlibcpp;
#define PI 3.1415926
int main()
{
double x0 = 0.0, y0 = 1.0, psi = 0.5, v = 2, L = 2, dt = 0.1;
double k = 1;
vector<vector<double>> ref_path(1000, vector<double>(3));
// 生成参考轨迹
vector<double> ref_x, ref_y;
for (int i = 0; i < 1000; i++)
{
ref_path[i][0] = 0.1 * i;
ref_path[i][1] = 2 * sin(ref_path[i][0]);
for (int i = 0; i < 999; i++) {
ref_path[i][2]= atan2((ref_path[i+1][1]-ref_path[i][1]),(ref_path[i+1][0]-ref_path[i][0]));
}
ref_x.push_back(ref_path[i][0]);
ref_y.push_back(ref_path[i][1]);
}
KinematicModel model(x0, y0, psi, v, L, dt);
vector<double> x_, y_;
vector<double> robot_state(4);
Stanley stanley(k);
for (int i = 0; i < 600; i++) {
plt::clf();
robot_state = model.getState();
vector<double> delta_index = stanley.stanleyControl(robot_state, ref_path);
model.updateState(0, delta_index[0]);
x_.push_back(model.x);
y_.push_back(model.y);
plt::plot(ref_x, ref_y, "b--");
plt::plot(x_, y_, "r");
plt::grid(true);
plt::ylim(-5, 5);
plt::pause(0.01);
if (delta_index[1] >= ref_path.size() - 1) break;
}
const char* filename = "./stanley.png";
plt::save(filename);
plt::show();
return 0;
}
3 Pure pursuit与Stanley算法对比
相同点:基于对前轮转角进行控制来消除横向误差
不同点:
PurePursuit算法:预瞄点的选取,距离越短,控制精度越高,但可能会产生震荡;预瞄距离越长,控制效果趋于平滑,震荡减弱。
Stanley算法:控制效果取决于控制增益,缺少纯追踪的规律性,调试需要花一定的精力寻找合适的控制增益值