基于Python3的数据结构与算法 - 02 冒泡排序和选择排序
一、列表排序
排序:将一组”无序“的记录序列调整为”有序“的记录序列。
列表排序:将无序的列表变为有序列表
- 输入:列表
- 输出:有序列表
- 升序与降序
- 内置排序函数:sort()
常见排序算法:
排序Low B三人组:
- 冒泡排序
- 选择排序
- 插入排序
排序NB三人组:
- 快速排序
- 堆排序
- 归并排序
其他排序:
- 希尔排序
- 计数排序
- 基数排序
1. 冒泡排序
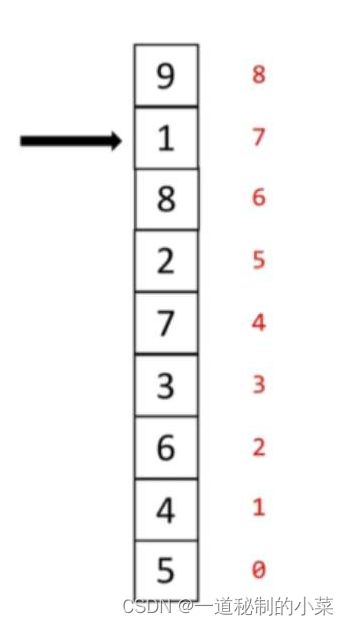
定义:列表每两个相邻的数,如果前面比后面大,则交换这两个数。(目的:得到一个升序列)
一趟排序完成后,则无序区减少一个数,有序区增加一个数。
代码关键点:趟、无序区范围。
我们可以发现,当最后仅剩下一个元素时不再需要排序,因此最大需要排序len(list)-1趟。
第一趟确定最大的数;第二趟确定第二大的数...
示例代码如下:
def bobble_sort(li):
for i in range(len(li) - 1): # 共循环n-1趟,第i趟
for j in range(len(li) - i - 1): # 箭头的长度是从0到len(li)-1;第j个箭头
if li[j] > li[j + 1]: # 若为降序,将 > 改为 <
li[j], li[j + 1] = li[j + 1], li[j]
print(li)
# li = [random.randint(1, 10000) for i in range(10)]
# print(li)
# bobble_sort(li)
# print(li) # 默认为升序的
bobble_sort([3, 2, 7, 5, 9, 6, 8, 4])我们可以发现冒泡算法的时间复杂度为:O(![]() )
)
我们可以发现,如果列表内已经有一部分已经排好序,那么我们可以简化算法:通过增加一个标志位提前结束循环。
冒泡排序 - 优化:
def bobble_sort(li):
for i in range(len(li) - 1): # 共循环n-1趟,第i趟
exchange = False # 增加一个标志位
for j in range(len(li) - i - 1): # 箭头的长度是从0到len(li)-1;第j个箭头
if li[j] > li[j + 1]: # 若为降序,将 > 改为 <
li[j], li[j + 1] = li[j + 1], li[j]
exchange = True # 每趟结束后,将值变为True;
print(li)
if not exchange: # 如果exchange值为真
return
bobble_sort([1, 2, 3, 4, 5, 9, 8, 7])2. 选择排序
思路:遍历一个列表,选择出最小的数,将其放到新列表当中,再对剩下的的元素继续遍历,再选择出一个最小的元素...重复以上的步骤。
选择排序简单版:
def select_sort_simple(li):
li_new = []
for i in range(len(li)): # 每次遍历找出一个最小数
min_val = min(li) # 找出最小数
li_new.append(min_val) #
li.remove(min_val)
return li_new
li = [3, 2, 4, 1, 5, 6, 8, 7, 9]
print(select_sort_simple(li))
缺点:
- 生成一个新的列表,占用内存空间大。
- min()和remove()的操作的复杂度不为1;而是O(n).
- 时间复杂度为O(
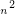 )
)
优化版:不创建一个新的列表,而是把挑选出来的最小的数值放到列表的最前面,而第一个数放到后面,与它交换位置。
示例代码如下:
def select_sort(li):
for i in range(len(li)-1): # i是第几趟
min_loc = i # 假定无序区的第一个数为最小值,让后面的数与其进行比较
for j in range(i+1, len(li)): # 确定无序区的范围
if li[j] < li[min_loc]: # 选择出最小追
min_loc = j # 最后确定min_loc是最小值
li[i], li[min_loc] = li[min_loc], li[i]
print(li)
li = [3, 2, 4, 1, 5, 6, 8, 7, 9]
print(li)
print("###")
select_sort(li) 复杂度也为O(![]() ),但是避免创建新列表。
),但是避免创建新列表。
流程:
- 一趟排序记录最小的数,放到第一个位置
- 再一趟排序记录列表无序区最小的数,放到第二个位置。
- 算法关键:确定有序区和无序区;确定无序区最小数的位置。