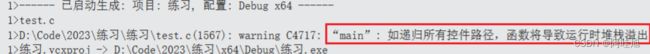「函数递归小课堂」~(C语言)
先赞后看,不足指正!
这将对我有很大的帮助!
所属专栏:C语言知识
阿哇旭的主页:Awas-Home page
目录
引言
1. 什么是递归?
2. 递归的限制条件
3. 递归应用举例
3.1 求 n 的阶乘
3.2 图例演示
3.3 代码实现
4. 递归问题
4.1 打印整数n的每一位
4.2 图例演示
4.3 代码实现
5. 递归与迭代
6. 知识拓展
7. 结语
引言
在前面,我们了解并学习到了关于C语言函数相关的概念知识,接下来我们将深入探究函数递归的奥秘。
那么,话不多说,我们一起来看看吧!
1. 什么是递归?
递归是我们学习C语言函数经常穿插的一个话题,那递归到底是何方神圣?
从字面意思理解起来不难,递归其实是一种解决问题的方法,在C语言中,递归就是函数自己调用自己。下面是一个简单的例子:
#include
int main()
{
printf("a-wax");
main(); //main函数自己调用自己
return 0;
} 上面举了一个最简单的函数递归例子,运行程序会陷入死递归,导致栈溢出(Stack overflow)。
2. 递归的限制条件
在我们使用递归的时候,不能让它无限的递归,在达到我们的要求时,就停止。因此,函数递归有两个必要条件:
- 递归存在限制条件,当满足这个限制条件的时候,递归便不再继续。
- 每次递归调用之后越来越接近这个限制条件。
3. 递归应用举例
3.1 求 n 的阶乘
在不考虑栈溢出的情况下,计算正整数 n 的阶乘。
阶乘公式:n ! = n * (n - 1) !
解题思路:n ! -> n * (n - 1) !
(n - 1) ! ->(n-1) * (n-2) !
......
通过这样,就可以把一个较大的问题,转换为一个与原问题相似,但规模较小的问题来解决。
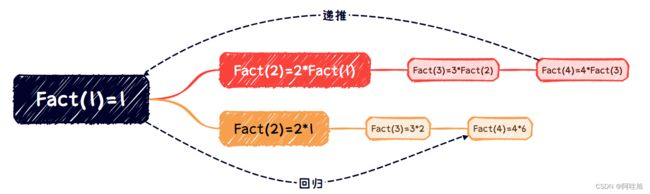
3.2 图例演示
3.3 代码实现
// 递归求n的阶乘
#include
int Fact(int n)
{
if (n == 0) //回归条件
return 1;
else //递推调用
return n * Fact(n - 1);
}
int main()
{
int n = 0;
printf("请输入要阶乘的数:\n");
scanf("%d", &n);
int ret = Fact(n);
printf("阶乘的结果:%d", ret);
return 0;
} 4. 递归问题
4.1 打印整数n的每一位
输入一个整数m,打印这个按照顺序打印整数的每一位。
例如:
输入:1014 输出:1 0 1 4
输入:220 输出:2 2 0
解题思路: 如果n是一位数,n的每一位就是n自己, n是超过一位数的话,就得拆分每一位。
我们可以发现数字的最低位是最容易得到的,通过%10就能得到。
此时,可以定义一个print函数来打印n的每一位数字。
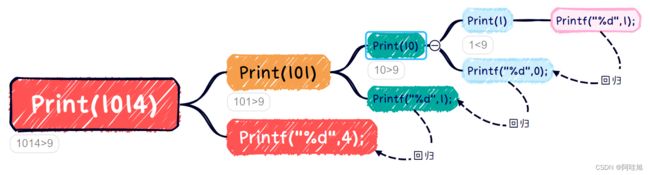
Print(n) 如果n是1014,那表⽰为 Print(1014) //打印1014的每⼀位 其中1014中的4可以通过%10得到,那么 Print(1014)就可以拆分为两步: 1. Print(1014/10) //打印101的每⼀位 2. printf(1014%10) //打印4 完成上述2步,那就完成了1014每⼀位的打印 那么Print(101)⼜可以拆分为Print(101/10) + printf(101%10)
4.2 图例演示
4.3 代码实现
//打印n的每一位
#include
void Print(int n)
{
if (n > 9) //回归条件
{
Print(n / 10); //递推调用
}
printf("%d ", n % 10);
}
int main()
{
int n = 0;
printf("请输入一个数:\n");
scanf("%d", &n);
Print(n);
return 0;
} 5. 递归与迭代
有时候,递归虽然好用,但也存在一些问题,就比如求第n位斐波那契数,是不适合用递归求解的。
#include
int Fibon(int n)
{
if (n <= 2)
return 1;
else
return Fibon(n - 1) + Fibon(n - 2);
}
int main()
{
int n = 0;
printf("请输入要求第几个斐波那契数:\n");
scanf("%d", &n);
int ret = Fibon(n);
printf("第%d个斐波那契数为%d\n", n, ret);
return 0;
} 当我们输入n位50的时候,需要很长时间才能算出结果,这也说明递归的写法是比较低效的,为什么呢?在递归计算过程中,会有重复计算,且递归层次越深,冗余计算就会越多,这就是导致效率低的主要原因。
此时,我们可以用迭代的方法来求解:
// 迭代求第n个斐波那契数
#include
int Fibon(int n)
{
// 中间变量
int a = 1;
int b = 1;
int c = 1;
if (n >= 3)
{
for (int i = 3; i <= n; i++)
{
c = a + b;
a = b;
b = c;
}
}
return c;
}
int main()
{
int n = 0;
printf("请输入要求第几个斐波那契数:\n");
scanf("%d", &n);
int ret = Fibon(n);
printf("第%d个斐波那契数为%d\n", n, ret);
return 0;
} 运行代码,我们会发现,速度明显比递归要快,效率更高。
6. 知识拓展
- 小青蛙跳台阶问题
- 汉诺塔问题
7. 结语
希望这篇文章对大家有所帮助,如果你有任何问题和建议,欢迎在评论区留言,这将对我有很大的帮助。
完结!咻~