【科学刷题】完全吃透所有树相关的算法题

1 二叉树

1.1 二叉树递归 / 层序遍历

1.1.1 二叉树的 对称 / 翻转 / 镜像

3个入门级简单题，汇总一下：

101. 对称二叉树

class Solution:
    def isSymmetric(self, root):
        # 56ms 击败10%
        # return self.check(root, root)
        if root is None:
            return True
        # 52ms 击败20%
        return self.check(root.left, root.right)

    def check(self, p, q):
        if p is None and q is None:
            return True
        if p is None or q is None:
            return False
        return p.val == q.val and self.check(p.left, q.right) and self.check(p.right, q.left)

226. 翻转二叉树

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if root is None:
            return None
        root.right, root.left = self.invertTree(root.left), self.invertTree(root.right)
        return root

剑指 Offer 27. 二叉树的镜像

class Solution:
    def mirrorTree(self, root: TreeNode) -> TreeNode:
        def recur(node):
            if node is None:
                return None
            node.left, node.right = recur(node.right), recur(node.left)
            return node
        return recur(root)

1.1.2 二叉树的直径 / 最大路径和

1.1.2.1 二叉树的直径

这种类型的题有两个关键步骤：

• 二叉树的直径
  • 更新：经过当前结点的最大长度
  • 返回：从当前结点出发的最大长度
• 二叉树中的最大路径和
  • 更新：经过当前结点的最大路径和
  • 返回：从当前结点出发的最大路径

543. 二叉树的直径

有空重新刷一下，注意边界条件

class Solution:
    def diameterOfBinaryTree(self, root: TreeNode) -> int:
        ans = 1
        def rec(node:TreeNode):
            nonlocal ans
            if node is None:
                return 0
            rl, rr = rec(node.left), rec(node.right)
            # 更新：经过当前结点的最大长度
            ans = max(ans, 1 + rl + rr)
            # 返回：从当前结点出发的最大长度
            return max(rl, rr) + 1
        
        rec(root)
        return ans - 1

1.1.2.2 二叉树中的最大路径和

124. 二叉树中的最大路径和

class Solution:
    def maxPathSum(self, root: TreeNode) -> int:
        ans = -inf
        def recursion(node)->int:
            nonlocal ans
            if node is None:
                return 0
            # 如果为负数，做一个截断
            left = max(0, recursion(node.left))
            right = max(0, recursion(node.right))
            # 更新：经过当前结点的最大路径和
            ans = max(ans, left + right + node.val)
            # 返回：从当前结点出发的最大路径
            return node.val + max(left, right)
        recursion(root)
        return ans

1.1.3 二叉树的最大 / 最小深度

最大深度

104. 二叉树的最大深度

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1 if root else 0

最小深度

111. 二叉树的最小深度

对于【二叉树的最小深度】，虽然BFS和DFS的时间复杂度相同，但一般来说BFS会更快，因为一般情况下只需要遍历部分结点即可返回

• DFS

class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        if root.left is None and root.right is None:
            return 1
        ans = inf
        if root.left:
            ans = min(ans, self.minDepth(root.left))
        if root.right:
            ans = min(ans, self.minDepth(root.right))
        return ans + 1

• BFS

class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root: return 0
        q = [(root, 1)]
        while q:
            top, d = q.pop(0)
            if top.left is None and top.right is None:
                return d
            if top.left:
                q.append((top.left, d + 1))
            if top.right:
                q.append((top.right, d + 1))

1.1.4 填充每个节点的下一个右侧节点指针

116. 填充每个节点的下一个右侧节点指针

• 递归

题目要求常数空间。

class Solution:
    def connect(self, root: 'Node') -> 'Node':
        if root is None:
            return None
        def recursion(node1, node2):
            if node1 is None or node2 is None:
                return
            node1.next = node2
            recursion(node1.left, node1.right)
            recursion(node2.left, node2.right)
            recursion(node1.right, node2.left)
        recursion(root.left, root.right)
        return root

• 层序遍历

跑起来快多了。。

class Solution:
    def connect(self, root: 'Node') -> 'Node':
        if root is None:
            return None
        queue = collections.deque()
        queue.append(root)
        while queue:
            sz = len(queue)
            pre = None
            for _ in range(sz):
                top = queue.popleft()
                if pre:
                    pre.next = top
                pre = top
                if top.left:
                    queue.append(top.left)
                if top.right:
                    queue.append(top.right)
        return root

117. 填充每个节点的下一个右侧节点指针 II

这题与上题不同，只能用BFS层序遍历求解了

1.1.5 二叉树的层序遍历

1.1.5.1 二叉树最大宽度

662. 二叉树最大宽度

class Solution:
    def widthOfBinaryTree(self, root: TreeNode) -> int:
        q = [(root, 0)]
        ans = 0
        max_width = 0
        while q:
            sz = len(q)
            lb, rb = inf, -inf
            for i in range(sz):
                top, idx = q.pop(0)
                lb = min(lb, idx)
                rb = max(rb, idx)
                max_width = max(max_width, (rb - lb + 1))
                if top.left:
                    q.append((top.left, idx * 2))
                if top.right:
                    q.append((top.right, idx * 2 + 1))

        return max_width

1.2 完全二叉树

1.2.1 复杂度${\log }^{2}N$的题目

这类题目有一个共同的特点:

1. 每次遍历都需要计算一遍二叉树左右子树的高度（复杂度$\log N$）
2. 然后结合这个高度信息，再去遍历左右子树（复杂度$\log N$）

二者叠加后，时间复杂度就变成了${\log }^{2}N$

1.2.1.1 完全二叉树的结点个数

222. 完全二叉树的节点个数

算法笔记：如何计算完全二叉树的节点数

利用完全二叉树的性质：

• 如果height_left == height_right
  • 是满二叉树，用公式计算结点数
• 否则
  • 用递归计算结点数

时间复杂度 $O(lo{g}^{2}N)$

class Solution:
    def countNodes(self, root: TreeNode) -> int:
        r = l = root
        hr = hl = 0
        while r is not None:
            hr += 1
            r = r.right
        while l is not None:
            hl += 1
            l = l.left
        # 空指针也会在这里返回
        if hl == hr:
            return 2 ** (hl) - 1
        return 1 + self.countNodes(root.left) + self.countNodes(root.right)

1.2.1.2 完全二叉树的最后一个节点

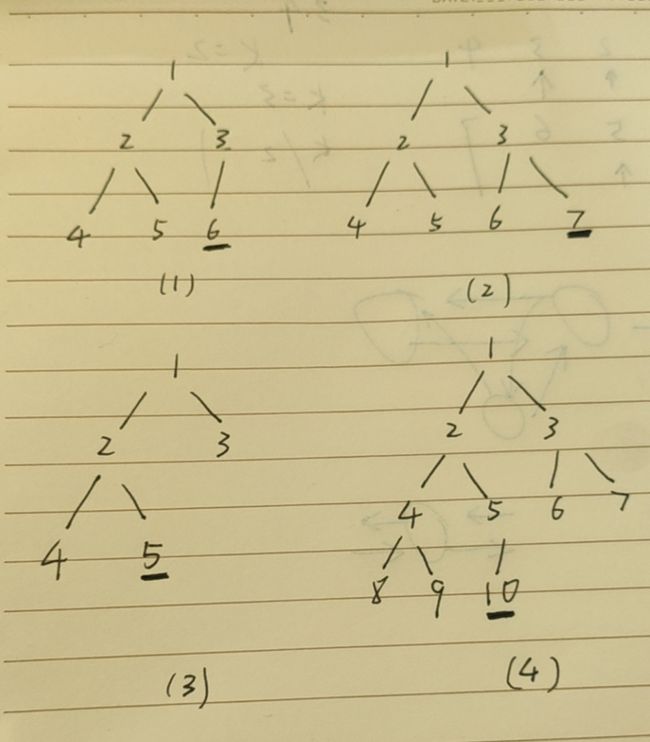
字节跳动面试题.完全二叉树的最后一个节点

实习｜算法岗血泪面经：商汤，旷世，阿里，字节跳动

这题的lh，rh与上题的区别：
lh：从左节点出发，一直往左走
rh：从右结点出发，一直往右左走

用这张图简单说明一下思路：

• 如果左子树高度>右子树高度，目标结点必然在左子树
• 如果左子树高度<=右子树高度，目标结点必然在右子树

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def getLastNode(root: TreeNode) -> TreeNode:
    if root is None or root.left is None:
        return root
    lp, rp = root.left, root.right
    lh = rh = 0
    while lp:
        lp = lp.left
        lh += 1
    while rp:
        rp = rp.left
        rh += 1
    if lh > rh:
        return getLastNode(root.left)
    elif lh <= rh:
        return getLastNode(root.right)

if __name__ == '__main__':
    case1 = TreeNode(1, TreeNode(2, TreeNode(4), TreeNode(5)),
                     TreeNode(3, TreeNode(6)))
    assert getLastNode(case1).val == 6
    case2 = TreeNode(1, TreeNode(2, TreeNode(4), TreeNode(5)),
                     TreeNode(3, TreeNode(6), TreeNode(7)))
    assert getLastNode(case2).val == 7
    case3 = TreeNode(1, TreeNode(2, TreeNode(4), TreeNode(5)),
                     TreeNode(3))
    assert getLastNode(case3).val == 5
    case4 = TreeNode(1,
                     TreeNode(2, TreeNode(4, TreeNode(8), TreeNode(9)), TreeNode(5, TreeNode(10))),
                     TreeNode(3, TreeNode(6), TreeNode(7)))
    assert getLastNode(case4).val == 1

1.2.2 完全二叉树的连续性性质

1.2.2.1 二叉树的完全性检验

958. 二叉树的完全性检验

class Solution:
    def isCompleteTree(self, root: TreeNode) -> bool:
        i = 0
        nodes = [(root, 1)]
        while i < len(nodes):
            node, v = nodes[i]
            i += 1
            if node:
                nodes.append([node.left, v * 2])
                nodes.append([node.right, v * 2 + 1])
        return len(nodes) == nodes[-1][1]

1.2.2.2 完全二叉树插入器

919. 完全二叉树插入器

class CBTInserter:

    def __init__(self, root: TreeNode):
        self.root = root
        queue = [root]
        self.heap = []
        while queue:
            top = queue.pop(0)
            self.heap.append(top)
            if top.left:
                queue.append(top.left)
            if top.right:
                queue.append(top.right)

    def insert(self, v: int) -> int:
        node = TreeNode(v)
        self.heap.append(node)
        n = len(self.heap)
        pid = n // 2 - 1
        parent = self.heap[pid]
        if n % 2:
            parent.right = node
        else:
            parent.left = node
        return parent.val

    def get_root(self) -> TreeNode:
        return self.root

1.3 二叉搜索树（BST）

1.3.1. BST的增删改查判断

手把手带你刷二叉搜索树（第二期）

手把手带你刷通二叉搜索树（第三期）

1.3.1.1. BST的查找 ⭐️

700. 二叉搜索树中的搜索

class Solution:
    def searchBST(self, root: TreeNode, val: int) -> TreeNode:
        if root is None or root.val == val:
            return root
        if root.val < val:
            return self.searchBST(root.right, val)
        else:
            return self.searchBST(root.left, val)

1.3.1.2. BST的插入 ⭐️⭐️

701. 二叉搜索树中的插入操作

class Solution:
    def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
        if root is None:
            return TreeNode(val)
        if root.val < val:
            root.right = self.insertIntoBST(root.right, val)
        else:
            root.left = self.insertIntoBST(root.left, val)
        return root

1.3.1.3. BST的删除 ⭐️⭐️⭐️⭐️

450. 删除二叉搜索树中的节点

1. 叶子结点（0个孩子） → 当场去世
2. 1个孩子 → 让孩子接替自己位置
3. 两个孩子 → 找到左子树中最大的结点或 [ 右子树最小结点 ] 接替自己

class Solution:
    def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
        if root is None:
            return None
        if root.val == key:
            # == 情况1 == & == 情况2 ==
            if root.left is None:
                return root.right
            if root.right is None:
                return root.left
            # == 情况3 ==
            # 找到右子树的最小结点，即右子树不断往左遍历的最后一个结点
            min_node = self.find_min(root.right) 
            # 【这个结点】和【待删除结点】做swap，但具体的操作形式为赋值：
            # 【待删除结点】.val = 【右子树最小结点】.val
            root.val = min_node.val
            # 转化为子问题：删除【右子树最小结点】
            root.right = self.deleteNode(root.right, min_node.val)
        elif root.val > key: # 左右顺序写错
            root.left = self.deleteNode(root.left, key)
        elif root.val < key:
            root.right = self.deleteNode(root.right, key)

        return root

    def find_min(self, root: TreeNode) -> TreeNode:
        while root.left:
            root = root.left
        return root

1.3.1.4 判断BST是否合法 ⭐️⭐️⭐️

面试题 04.05. 合法二叉搜索树

98. 验证二叉搜索树

我们通过使用辅助函数，增加函数参数列表，在参数中携带额外信息，将这种约束传递给子树的所有节点，这也是二叉树算法的一个小技巧吧。

class Solution:
    # def isValidBST(self, root: TreeNode) -> bool:
    def isValidBST(self, root: TreeNode, min_: TreeNode = None, max_: TreeNode = None) -> bool:
        if root is None:
            return True
        if min_ is not None and root.val <= min_.val:
            return False
        if max_ is not None and root.val >= max_.val:
            return False
        return self.isValidBST(root.left, min_, root) and \
               self.isValidBST(root.right, root, max_)

1.3.2. BST 带上下界的函数

这个专题的题目其实在本文的其他部分都有收录，但笔者发现了这些题的共通之处，故做一整理。

本专题为几道涉及BST的的题目，且解题函数中都涉及到了lower、upper参数，这两个参数会在递归过程中判断当前结点是否是调用方的一个合法子结点（left or right），如果不是，会返回None

1.3.2.1 前序遍历构造二叉搜索树

1008. 前序遍历构造二叉搜索树

class Solution:
    def bstFromPreorder(self, preorder: List[int]) -> TreeNode:
        index = 0
        N = len(preorder)

        def dfs(lower, upper):
            nonlocal index
            if not 0 <= index < N:
                return None
            if preorder[index] < lower or preorder[index] > upper:
                return None
            cur = preorder[index]
            node = TreeNode(cur)
            index += 1
            node.left = dfs(lower, cur)
            node.right = dfs(cur, upper)
            return node

        return dfs(-inf, inf)

1.3.2.2. BST的序列化和反序列化

449. 序列化和反序列化二叉搜索树

• 与1.6.1相比：
  • serialize：如果为None，不需要单独转义为特定字符，而可以直接pass
  • deserialize：采用类似1.8.2.1 前序 $\to$ 构造BST的做法，用lower和upper界定当前index的元素是否合法

class Codec:
    def serialize(self, root: TreeNode) -> str:
        def helper(root):
            if root is None: return []
            left = helper(root.left)
            right = helper(root.right)
            return [str(root.val)] + left + right
        return ",".join(helper(root))
        

    def deserialize(self, data: str) -> TreeNode:
        if not data: return None
        seq = [int(x) for x in data.split(",")]
        def helper(lower=-inf, upper=inf):
            nonlocal seq
            if not seq or (not lower<seq[0]<upper):
                return None
            root = TreeNode(seq.pop(0))
            root.left = helper(lower, root.val)
            root.right = helper(root.val, upper)
            return root
        return helper()

1.3.2.3 判断BST是否合法

面试题 04.05. 合法二叉搜索树

98. 验证二叉搜索树

class Solution:
    # def isValidBST(self, root: TreeNode) -> bool:
    def isValidBST(self, root: TreeNode, lower: TreeNode = None, upper: TreeNode = None) -> bool:
        if root is None:
            return True
        if lower is not None and root.val <= lower.val:
            return False
        if upper is not None and root.val >= upper.val:
            return False
        return self.isValidBST(root.left, lower, root) and \
               self.isValidBST(root.right, root, upper)

1.3.2.4 修剪BST

669. 修剪二叉搜索树

class Solution:
    def trimBST(self, root: TreeNode, low: int, high: int) -> TreeNode:
        if root is None:
            return None
        if root.val < low:
            return self.trimBST(root.right, low, high)
        elif root.val > high:
            return self.trimBST(root.left, low, high)
        else:
            root.left = self.trimBST(root.left, low, high)
            root.right = self.trimBST(root.right, low, high)
            return root

1.3.3. BST中序遍历的性质

手把手带你刷二叉搜索树（第一期）

1.3.3.1 二叉搜索树中第K小的元素

230. 二叉搜索树中第K小的元素

时间复杂度 $O(K)$

class Solution:
    def kthSmallest(self, root: TreeNode, k: int) -> int:
        rank = 0
        ans = -1

        def rec(node: TreeNode):
            nonlocal rank, ans
            if node is None:
                return
            rec(node.left)
            rank += 1
            if rank == k:
                ans = node.val
                return
            rec(node.right)

        rec(root)
        return ans

1.3.3.2 二叉搜索树的第k大节点

剑指 Offer 54. 二叉搜索树的第k大节点

面试题54. 二叉搜索树的第 k 大节点（中序遍历 + 提前返回，清晰图解）

题解的Python代码用类变量代替了我答案的局部变量，值得学习

class Solution:
    def kthLargest(self, root: TreeNode, k: int) -> int:
        cnt = 0
        ans = None
        def travel(node):
            nonlocal cnt, ans
            if node is None or cnt > k:
                return 
            travel(node.right)
            cnt += 1
            if cnt == k:
                ans = node
            travel(node.left)
        
        travel(root)
        return ans.val

1.3.3.3 把二叉搜索树转换为累加树

538. 把二叉搜索树转换为累加树

同样利用了BST中序遍历递增的性质

class Solution:
    def convertBST(self, root: TreeNode) -> TreeNode:
        sum_ = 0

        def rec(node: TreeNode):
            nonlocal sum_
            if node is None:
                return None
            rec(node.right)
            sum_ += node.val
            node.val = sum_
            rec(node.left)

        rec(root)
        return root

1.3.3.4 二叉搜索树中的众数

501. 二叉搜索树中的众数

# 一次遍历得到结果
class Solution:
    def findMode(self, root: TreeNode) -> List[int]:
        ans = []
        cnt = 0
        pre = nan
        max_cnt = 0

        def rec(root):
            nonlocal ans, cnt, pre, max_cnt
            if root is None:
                return
            rec(root.left)
            # travel
            cur = root.val
            if cur == pre:
                cnt += 1
            else:
                cnt = 1
            pre = cur
            if cnt > max_cnt:
                max_cnt = cnt
                ans = [cur]
            elif cnt == max_cnt:
                ans.append(cur)
            # end travel
            rec(root.right)

        rec(root)
        return ans

1.3.4 恢复swap一次的BST

99. 恢复二叉搜索树

方法一、显式中序遍历

之前刷东哥算法小抄的时候刷到了这个题，在没看题解的情况下写了个时间复杂度$O(N\log N)$的代码，解法特别高效，中序遍历后，排序，再中序遍历一次。

如果用【显式中序遍历】方法的话，需要用for循环找到是哪两个结点乱序了，然后交换两个结点的值就好了。

class Solution:
    def recoverTree(self, root: TreeNode) -> None:
        seq = []

        def inorder(root):
            if not root:
                return
            inorder(root.left)
            seq.append(root)
            inorder(root.right)

        inorder(root)
        x = y = None
        n = len(seq)
        # 那[3,2,1]的例子推这个步骤
        for i in range(n - 1):
            if seq[i].val > seq[i + 1].val:
                y = seq[i + 1]
                if x is None:
                    x = seq[i]
                else:
                    break
        x.val, y.val = y.val, x.val

1.3.5. BST与子树

1373. 二叉搜索子树的最大键值和

美团面试官：你对后序遍历一无所知

class Solution:
    def maxSumBST(self, root: TreeNode) -> int:
        self.ans = -inf

        def travel(root):
            if root is None:
                return inf, -inf, 0, True
            left_min, left_max, left_sum, left_valid = travel(root.left)
            right_min, right_max, right_sum, right_valid = travel(root.right)
            if left_valid and right_valid and left_max < root.val < right_min:
                cur_sum = left_sum + right_sum + root.val
                self.ans = max(self.ans, cur_sum)
                return min(left_min,root.val), max(right_max,root.val), cur_sum, True
            else:
                return 0, 0, 0, False

        travel(root)
        return max(self.ans,0)

1.4 平衡二叉树

判断平衡二叉树

剑指 Offer 55 - II. 平衡二叉树

面试题55 - II. 平衡二叉树（从底至顶、从顶至底，清晰图解）

递归判断：左右子树高度差 < 2

类似于二叉树的后序遍历

class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        def recur(root):
            if root is None:
                return 0
            left = recur(root.left)
            right = recur(root.right)
            if left==-1 or right==-1:
                return -1
            if abs(right-left)>=2:
                return -1
            return max(left, right) + 1
        return recur(root)!=-1

创建平衡树

面试题 04.02. 最小高度树

• 一行python

return TreeNode(nums[len(nums) // 2], self.sortedArrayToBST(nums[:len(nums) // 2]), 
self.sortedArrayToBST(nums[len(nums) // 2 + 1:])) if nums else None

1.5 二叉树的【子结构 / 子树】匹配

首先阐述一个概念：子结构匹配与子树匹配

子树匹配：

子树匹配就是A的子结构与B完全匹配

子结构匹配：

子结构匹配就是A的子结构与B部分匹配，A的子结构允许有与B不匹配的其他结构

如何判断是【子树匹配】还是【子结构】呢？我觉得最重要的还是读题。

并且这两个匹配算法在代码上相差比较小，如果用某种方法A不了我们可以想想是不是思考错题意了

1.5.1 子结构匹配

剑指 Offer 26. 树的子结构

建议看这个题解：

面试题26. 树的子结构（先序遍历 + 包含判断，清晰图解）

例如:
给定的树 A:

     3
    / \
   4   5
  / \
 1   2
给定的树 B：

   4 
  /
 1

recur判定函数的记忆方法：

• 如果B为空，说明走到底了，True
• 如果A为空，说明没救了，False
• 判断元素是否相等
• 继续往下递归（and条件）

递归里面有递归，很难想到

def recur(A, B):
    if B is None:
        return True
    if A is None:
        return False
    if not A.val==B.val:
        return False
    return recur(A.left, B.left) and recur(A.right, B.right) # and

class Solution:
    def isSubStructure(self, A: TreeNode, B: TreeNode) -> bool:
        # bool
        return bool(A and B) and ( recur(A, B) or self.isSubStructure(A.left, B) or self.isSubStructure(A.right, B) )

1.5.2 子树匹配

572. 另一个树的子树

这题如果是子结构匹配的话，示例2是可以通过的（但子树匹配的返回值为false）。我们做题的第一件事就是理解题意。

这题其实可以复用上题的代码，就是需要修改一下recur函数的判断条件

【子结构匹配】的recur函数：

def recur(A, B):
    if B is None: # 只要到了B的边界（None值）就视为完成了匹配
        return True
    if A is None:
        return False
    if not A.val==B.val:
        return False
    return recur(A.left, B.left) and recur(A.right, B.right) # and

【子树匹配】的recur函数：

def recur(A, B):
    if A is None and B is None: # B到了边界时，A必须也到边界
        return True
    if bool(A) ^ bool(B): # 如果AB其中之一为None，另外一个不为None，就表明匹配失败
        return False
    if not A.val==B.val:
        return False
    return recur(A.left, B.left) and recur(A.right, B.right)

相同点：

AB都不为None，值（val）不匹配，返回False

不同点：(加粗)

A	B	子树匹配	子结构匹配
None	not None	False	False
None	None	True	True
not None	None	False	True

子树匹配完整代码：

def recur(A, B):
    if A is None and B is None:
        return True
    if bool(A) ^ bool(B):
        return False
    if not A.val==B.val:
        return False
    return recur(A.left, B.left) and recur(A.right, B.right)


class Solution:
    def isSubtree(self, A: TreeNode, B: TreeNode) -> bool:
        return bool(A and B) and ( recur(A, B) or self.isSubtree(A.left, B) or self.isSubtree(A.right, B) )

1.5.3 查找所有重复子树

652. 寻找重复的子树

东哥笔记：

手把手带你刷二叉树（第三期）

本质上是数的后序遍历，使用了序列化的技巧

class Solution:
    NULL = "#"

    def findDuplicateSubtrees(self, root: TreeNode) -> List[TreeNode]:
        memo = collections.defaultdict(int)
        res = []

        def traverse(node: TreeNode):
            if node is None:
                return self.NULL
            seq = ",".join([traverse(node.left), traverse(node.right), str(node.val)])
            if memo[seq] == 1:  # 巧妙地去重
                res.append(node)
            memo[seq] += 1
            return seq

        traverse(root)
        return res

1.6 序列化与反序列化

1.6.1 二叉树的序列化与反序列化

297. 二叉树的序列化与反序列化

二叉树的题，就那几个框架，枯燥至极

1.6.1.1 先序遍历

class Codec:
    NULL = '#'

    def serialize(self, root: TreeNode) -> str:
        res = []

        def traverse(root: TreeNode):
            if root is None:
                res.append(self.NULL)
            else:
                res.append(str(root.val))
                traverse(root.left)
                traverse(root.right)

        traverse(root)
        return ','.join(res)

    def deserialize(self, data: str) -> TreeNode:
        lst = data.split(',')

        def traverse():
            val = lst.pop(0)
            if val == self.NULL:
                return None
            else:
                node = TreeNode(int(val))
                node.left = traverse()
                node.right = traverse()
                return node

        return traverse()

1.6.1.2 后序遍历

• serialize 部分，调换顺序为后序遍历
• deserialize部分，做两点改动：
  • 每次pop最后一个元素（具体到Python的list对象，就是val = lst.pop()）
  • 先左后右 $\to$ 先左后右

class Codec:
    NULL = '#'

    def serialize(self, root: TreeNode) -> str:
        res = []

        def traverse(root: TreeNode):
            if root is None:
                res.append(self.NULL)
            else:
                traverse(root.left)
                traverse(root.right)
                res.append(str(root.val))
                
        traverse(root)
        return ','.join(res)

    def deserialize(self, data: str) -> TreeNode:
        lst = data.split(',')

        def traverse():
            # 与中序不同，取出最后的元素
            val = lst.pop()
            if val == self.NULL:
                return None
            else:
                node = TreeNode(int(val))
                # 先右后左
                node.right = traverse()
                node.left = traverse()
                
                return node

        return traverse()

1.6.1.3 中序遍历

1.6.1.4 层序遍历

• labladong 做法

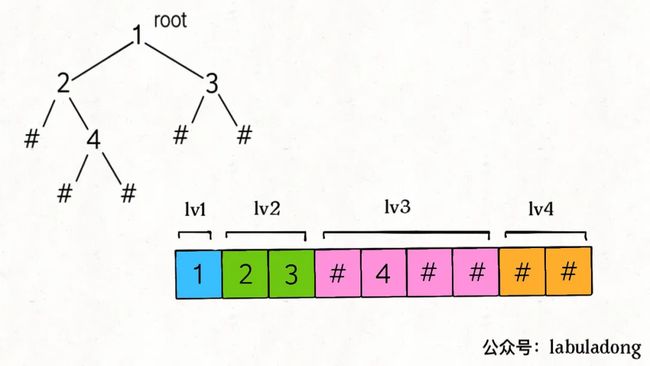
class Codec:
    NULL = '#'

    def serialize(self, root: TreeNode) -> str:
        q = collections.deque()
        q.append(root)
        seq = []
        while q:
            top = q.popleft()
            seq.append(str(top.val) if top else self.NULL)
            if top is not None:
                q.append(top.left)
                q.append(top.right)
        return ",".join(seq)

    def deserialize(self, data: str) -> TreeNode:
        def decode(elem: str) -> Optional[TreeNode]:
            if elem == self.NULL:
                return None
            return TreeNode(int(elem))

        seq = data.split(",")
        q = collections.deque()
        root = decode(seq.pop(0))
        q.append(root)
        while q and seq:
            top = q.popleft()
            if top is not None:
                left = decode(seq.pop(0))
                right = decode(seq.pop(0))
                top.left = left
                top.right = right
                q.append(left)
                q.append(right)
        return root

• leetcode做法
  • 与labuladong做法的两个区别
    • 1 — 删除后导null
    • 2 — decode时，如果seq为空，返回None

class Codec:
    NULL = 'null'

    def serialize(self, root: TreeNode) -> str:
        q = collections.deque()
        q.append(root)
        seq = []
        while q:
            top = q.popleft()
            seq.append(str(top.val) if top else self.NULL)
            if top is not None:
                q.append(top.left)
                q.append(top.right)
        # 删除后导null
        index = len(seq) - 1
        while index >= 0 and seq[index] == self.NULL: index -= 1
        seq = seq[:index + 1]
        print(seq)
        return "[" + ",".join(seq) + "]"

    def deserialize(self, data: str) -> TreeNode:
        
        def decode(seq) -> Optional[TreeNode]:
            if not seq:
                return None
            elem = seq.pop(0)
            if elem == self.NULL:
                return None
            return TreeNode(int(elem))

        if data == "[]": return None
        seq = data[1:-1].split(",")
        q = collections.deque()
        root = decode(seq)
        q.append(root)
        while q and seq:
            top = q.popleft()
            if top is not None:
                left = decode(seq)
                right = decode(seq)
                top.left = left
                top.right = right
                q.append(left)
                q.append(right)
        return root

1.6.2 BST的序列化和反序列化

449. 序列化和反序列化二叉搜索树

• 与1.6.1相比：
  • serialize：如果为None，不需要单独转义为特定字符，而可以直接pass
  • deserialize：采用类似1.8.2.1 前序 $\to$ 构造BST的做法，用lower和upper界定当前index的元素是否合法

class Codec:
    def serialize(self, root: TreeNode) -> str:
        def helper(root):
            if root is None: return []
            left = helper(root.left)
            right = helper(root.right)
            return [str(root.val)] + left + right
        return ",".join(helper(root))
        

    def deserialize(self, data: str) -> TreeNode:
        if not data: return None
        seq = [int(x) for x in data.split(",")]
        def helper(lower=-inf, upper=inf):
            nonlocal seq
            if not seq or (not lower<seq[0]<upper):
                return None
            root = TreeNode(seq.pop(0))
            root.left = helper(lower, root.val)
            root.right = helper(root.val, upper)
            return root
        return helper()

1.6.3 查找所有重复子树

652. 寻找重复的子树

东哥笔记：

手把手带你刷二叉树（第三期）

本质上是数的后序遍历，使用了序列化的技巧

class Solution:
    NULL = "#"

    def findDuplicateSubtrees(self, root: TreeNode) -> List[TreeNode]:
        memo = collections.defaultdict(int)
        res = []

        def traverse(node: TreeNode):
            if node is None:
                return self.NULL
            seq = ",".join([traverse(node.left), traverse(node.right), str(node.val)])
            if memo[seq] == 1:  # 巧妙地去重
                res.append(node)
            memo[seq] += 1
            return seq

        traverse(root)
        return res

1.7 二叉树【序的转换 / 根据序重建树】

https://www.cnblogs.com/TQCAI/p/8546737.html

这个类型的题，一般以下几种出题方法：

1. 给出其中两个序，求另外一个序。如：前序和中序，求后序
2. 给出两个序，要求重建二叉树

1.7.1 中序 + 前序 / 后序 $\to$ 建树 / 建序

1.7.1.1 中序 + 前序 $\to$ 建树

105. 从前序与中序遍历序列构造二叉树

preorder的最开始的元素就是根节点元素：preorder[pre_s]

找到inorder中的下标：i = inorder.index(preorder[pre_s])

左子树元素数量：num_left = i - in_s

递归：

• 左子树
  • preorder range: pre_s + 1, pre_s + num_left
  • inorder range: in_s, i - 1
• 右子树
  • preorder range: pre_s + num_left + 1, pre_e
  • inorder range: i + 1, in_e

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        def build(pre_s, pre_e, in_s, in_e):
            if pre_s > pre_e or in_s > in_e:
                return None
            if pre_s == pre_e:
                return TreeNode(preorder[pre_s])
            i = inorder.index(preorder[pre_s])
            num_left = i - in_s
            node = TreeNode(preorder[pre_s])
            node.left = build(pre_s + 1, pre_s + num_left, in_s, i - 1)
            node.right = build(pre_s + num_left + 1, pre_e, i + 1, in_e)
            return node

        N = len(inorder)
        return build(0, N - 1, 0, N - 1)

1.7.1.2 中序 + 后序 $\to$ 建树

106. 从中序与后序遍历序列构造二叉树

class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
        def build(post_s, post_e, in_s, in_e):
            if post_s > post_e or in_s > in_e:
                return None
            if post_s == post_e:
                return TreeNode(postorder[post_e])
            i = inorder.index(postorder[post_e])
            num_left = i - in_s
            node = TreeNode(postorder[post_e])
            node.left = build(post_s, post_s + num_left - 1, in_s, i - 1)
            node.right = build(post_s + num_left, post_e - 1, i + 1, in_e)
            return node

        N = len(inorder)
        return build(0, N - 1, 0, N - 1)

1.7.2 前序 + 后序 $\to$ 建中序 / 树计数

多年前还在学土木时写的：分析报告

• 前序 + 后序 $\to$ 建中序

     1
    / \
   2   4
 /  \    \
3   5     6  

pre: 1 [2 3 5] [4 6]
post: [3 5 2] [6 4] 1

如果满足i == postE - 1，就说明当前结点既可以是左子树，也可以是右子树（paradox结点）

int pre[LEN] = {8, 5, 2, 6, 10, 9, 11};
int in[LEN];
int post[LEN] = {2, 6, 5, 9, 11, 10, 8};
int t = 0;
int flag = 1;

void setIn(int preS, int preE, int postS, int postE) {
    if (preS == preE) {
        in[t++] = pre[preS];
        return;
    }
    //finding the elem which is the root of left sub_tree
    int i = postS;
    while (i <= postE && post[i] != pre[preS + 1]) i++;
    //calculate the numbers of left sub_tree
    int leftNum = i - postS + 1;
    //is paradox
    if (i == postE - 1) {
        flag = 0;
        setIn(preS + 1, preS + leftNum, postS, i);//default consider this is a right leaf
        in[t++] = pre[preS];
        return;
    }
    //build the in_order traversal sequence
    setIn(preS + 1, preS + leftNum, postS, i);
    in[t++] = pre[preS];
    setIn(preS + leftNum + 1, preE, i + 1, postE - 1);
}

setIn(0, n - 1, 0, n - 1);

实战一下：889. 根据前序和后序遍历构造二叉树

class Solution:
    def constructFromPrePost(self, pre: List[int], post: List[int]) -> TreeNode:
        N = len(pre)
        if N == 0:
            return None
        if N == 1:
            return TreeNode(pre[0])
        # 左子树根节点
        left_root = pre[1]
        # 算出左子树结点数
        n_left = post.index(left_root) + 1
        return TreeNode(
            pre[0],
            self.constructFromPrePost(pre[1:1 + n_left], post[:n_left]),
            self.constructFromPrePost(pre[1 + n_left:], post[n_left:-1]),
        )

• 前序 + 后序 $\to$ 判断有多少可能的树

int cnt;

void calc(int preS, int preE, int postS, int postE) {
    if (preS >= preE) return;
    int i = postS;
    while (i <= postE - 1 && post[i] != pre[preS + 1]) i++;
    int ln = i - postS + 1;    //left_num
    if (i == postE - 1) cnt++;
    calc(preS + 1, preS + ln, postS, postS + ln - 1);
    calc(preS + ln + 1, preE, postS + ln, postE - 1);
}

在上文模板的基础上，在检测到有一组结点既可以当左子树，又可以当右子树时，cnt++（记录这样的结点出现的个数）。最后输出cnt的二次幂（假如有一个这样的结点，那就有左右两种形态。如果有两个，在控制左右形态的同时，左右又各有左右两种形态，一次类推，比图cnt=3 ,ans就等于8 ……）

最后结果：$ans=cn{t}^2$

1.8 二叉树与单调性

1.8.1 最大二叉树

654. 最大二叉树

参考一个$O(N)$的题解：最大二叉树

# inf | 3 2 1 6 0 5
# 找从当前往左第一个比当前元素大的
# 3->inf
# 2->3
# 1->2
# 6->inf
# 0->6
# 5->6
def build(nums: List[int], parent: TreeNode, index: int):
    while 0 <= index < len(nums):
        if nums[index] < parent.val:
            now = TreeNode(nums[index])
            # 如果当前结点有右结点，说明是回溯回来的
            # tmp 比parent小，也比now小
            tmp = parent.right
            parent.right = now
            now.left = tmp
            # end
            index = build(nums, now, index + 1)
        else:
            # 将index透传给上一个调用点
            return index
    return -1


class Solution(object):
    def constructMaximumBinaryTree(self, nums):
        parent = TreeNode(inf)
        build(nums, parent, 0)
        return parent.right

1.8.2 前序/后序 $\to$ 构造/判断 BST

1.8.2.1 前序 $\to$ 构造BST

1008. 前序遍历构造二叉搜索树

首先可以想到两种时间复杂度为$O(N\log N)$的方法：

1. BST的中序序列是有序的。故对preorder进行排序【$O(N\log N)$】，就能得到inorder。然后根据preorder+inorder 就能得到结果【$O(N)$】
2. 根节点为preorder[start]，根据BST的性质，根节点的左子树全部小于root.val。如果是线性查找，时间复杂度为$O(N^2)$，如果是二分查找，时间复杂度为$O(N\log N)$

然后，我们看两种时间复杂度为$O(N)$的方法：

• 递归的方法：

class Solution:
    def bstFromPreorder(self, preorder: List[int]) -> TreeNode:
        index = 0
        N = len(preorder)

        def dfs(lb, ub):
            nonlocal index
            if not 0 <= index < N:
                return None
            if preorder[index] < lb or preorder[index] > ub:
                return None
            cur = preorder[index]
            node = TreeNode(cur)
            index += 1
            node.left = dfs(lb, cur)
            node.right = dfs(cur, ub)
            return node

        return dfs(-inf, inf)

• 非递归的方法（单调栈）：

自己在草稿纸上推一下，只要知道是【单调递减】栈就行了

class Solution:
    def bstFromPreorder(self, preorder: List[int]) -> TreeNode:
        root = TreeNode(preorder[0])
        stack = [root]
        for num in preorder[1:]:
            node = TreeNode(num)
            top = None
            # 不满足【单调递减栈】的条件
            while stack and not (num < stack[-1].val):
                top = stack.pop()
            if top is None:
                stack[-1].left = node
            else:
                top.right = node
            stack.append(node)
        return root

1.8.2.2 前序/后序 $\to$ 判断BST

对于这种类型的题，即给一个 前序/后序 的序列，判断是否为BST的 前序/后序 的序列。最开始可以想到一种比较朴素的想法：

不妨设已知preorder，则root.val = preorder[start]，则可以找到r_start = lower_bound(preorder[start+1:], root.val)，只要保证preorder[start+1:r_start]且preorder[r_start:]>root.val，并且递归地判断这一结论，就可以得出最终的结论。

但这么做的时间复杂度为$O(N^2)$ — java 两种解法

但我们可以结合BST的结论，然后牢记这两个原则，就可以一举解决以下两道题了：

• BST的 preorder ：入栈递减，出栈递增
• BST的postorder：出栈递增，入栈递减

BST的postorder看的是倒序

如何判断：在遍历元素时，与出栈序列的栈顶进行判断，如果不满足就返回False

1.8.2.2.1 前序 $\to$ 判断BST

255. 验证前序遍历序列二叉搜索树

题解：Python3 图解，栈

入栈递减，出栈递增

class Solution:
    def verifyPreorder(self, preorder: List[int]) -> bool:
    	# 出栈序列的栈顶
        top = -inf
        # 单调递减 栈
        stack = []
        for val in preorder:
        	# 不满足【出栈递增】的条件，即小于了出栈序列的栈顶
            if val < top:
                return False
            # 不满足【单调递减】栈的条件
            while stack and (not stack[-1] > val):
            	# 出栈序列的栈顶
                top = stack.pop()
            stack.append(val)
        return True

1.8.2.2.2 后序 $\to$ 判断BST

剑指 Offer 33. 二叉搜索树的后序遍历序列

题解：面试题33. 二叉搜索树的后序遍历序列（递归分治 / 单调栈，清晰图解）

class Solution:
    def verifyPostorder(self, postorder: List[int]) -> bool:
    	# 出栈序列的栈顶
        top = inf
        # 单调递增 栈
        stack = []
        for val in postorder[::-1]:
        	# 不满足【出栈递减】的条件，即小于了出栈序列的栈顶
            if val > top:
                return False
            # 不满足【单调递增】栈的条件
            while stack and (not stack[-1] < val):
            	# 出栈序列的栈顶
                top = stack.pop()
            stack.append(val)
        return True

1.9 二叉树的非递归迭代

史上最全遍历二叉树详解

1.9.1 非递归先序

144. 二叉树的前序遍历

官方题解

• LC官方 / 王道数据结构 的解法

class Solution:
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        stack = []
        ans = []
        while root or stack:
            while root:
            	# 访问
                ans.append(root.val)
                # 入栈，向左遍历
                stack.append(root)
                root = root.left
            # 出栈，向右遍历
            root = stack.pop()
            root = root.right
        return ans

• 一种更能被理解的解法，但不能泛化到中序中

class Solution:
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        if not root: return []
        stack = [root]
        ans = []
        while stack:
            curr = stack.pop()
            ans.append(curr.val)
            left, right = curr.left, curr.right
            if right:
                stack.append(right)
            if left:
                stack.append(left)

        return ans

1.9.2 非递归中序

94. 二叉树的中序遍历

官方题解

class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        stack = []
        ans = []
        while root or stack:
            while root:
            	# 入栈，向左遍历
                stack.append(root)
                root = root.left
            # 出栈
            root = stack.pop()
            # 访问
            ans.append(root.val)
            # 向右遍历
            root = root.right
        return ans

1.9.3 非递归后序

145. 二叉树的后序遍历

官方题解

最简单的想法就是利用后序遍历的性质：倒序是先右后左的先序遍历

class Solution:
    def postorderTraversal(self, root: TreeNode) -> List[int]:
        stack = []
        ans = []
        while root or stack:
            while root:
                ans.append(root.val)
                stack.append(root)
                root = root.right
            root = stack.pop()
            root = root.left
        return ans[::-1]

1.10 最近公共祖先（LCA）

1.10.1 二叉树的LCA

1.10.1.1 两结点都在树中

236. 二叉树的最近公共祖先

class Solution:
    def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:
    	# 直接对TreeNode对象进行判断就ok，甚至不需要对TreeNode.val进行判断
        if root in [p, q, None]: 
            return root
        l_ret = self.lowestCommonAncestor(root.left, p, q)
        r_ret = self.lowestCommonAncestor(root.right, p, q)
        if l_ret is None and r_ret is None:
            return None
        if l_ret is not None and r_ret is not None:
            return root
        return l_ret if l_ret else r_ret

1.10.1.2 某一结点不在树中

1644. 二叉树的最近公共祖先 II

上一题的代码是不能用在这题的。为什么呢，观察代码会发现，如果p在树中而q不在树中，会把p当做LCA返回。

c++几乎双百的递归解法

以下为解题思路，本质仍为后序遍历：

• 需要保存ans为类对象
• 递归函数dfs，返回值为bool：当前子树是否包含p或q。
  • 判断当前子树是否包含p或q：
    • 如果左右子树之一的递归结果为True，or
    • 当前结点的值为p, q
  • 在递归过程中，顺便更新结果：
    • 如果左右子树都含p, q，说明当前结点为ans
    • 如果当前结点==p or ==q，且某个子树含p, q，说明当前结点为ans

class Solution:
    def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:
        self.ans: Optional[TreeNode] = None
        self.dfs(root, p, q)
        return self.ans

    def dfs(self, root: TreeNode, p: TreeNode, q: TreeNode) -> bool:
        if root is None:
            return False
        l_ret: bool = self.dfs(root.left, p, q)
        r_ret: bool = self.dfs(root.right, p, q)
        if l_ret and r_ret:
            self.ans = root
        if (l_ret or r_ret) and (root.val in [p.val, q.val]):
            self.ans = root
        if l_ret or r_ret:
            return True
        if root.val in [p.val, q.val]:
            return True
        return False

1.10.1.3 含parent结点

1650. 二叉树的最近公共祖先 III

class Solution:
    def lowestCommonAncestor(self, p: 'Node', q: 'Node') -> 'Node':
        a, b = p, q
        while a != b:
            a = a.parent if a else q
            b = b.parent if b else p
        return a

1.10.1.4 两结点泛化为多结点

1676. 二叉树的最近公共祖先 IV

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', nodes: 'List[TreeNode]') -> 'TreeNode':
    	# 直接对TreeNode对象进行判断就ok，甚至不需要对TreeNode.val进行判断
        if root in nodes + [None]: 
            return root
        l_ret = self.lowestCommonAncestor(root.left, nodes)
        r_ret = self.lowestCommonAncestor(root.right, nodes)
        if l_ret is None and r_ret is None:
            return None
        if l_ret is not None and r_ret is not None:
            return root
        return l_ret if l_ret else r_ret

1.10.1.5 最深叶节点的LCA

1123. 最深叶节点的最近公共祖先

「一题双解」递归优化

• 两次递归

class Solution:
    depth = {}

    def lcaDeepestLeaves(self, root: TreeNode) -> TreeNode:
        self.build_depth(root)
        return self.get_lca(root)

    def get_lca(self, root):
        if root is None:
            return None
        l_depth = self.get_depth(root.left)
        r_depth = self.get_depth(root.right)
        if l_depth == r_depth:
            return root
        elif l_depth < r_depth:
            return self.get_lca(root.right)
        else:
            return self.get_lca(root.left)

    def get_depth(self, root):
        if root is None:
            return 0
        else:
            return self.depth[root.val]

    def build_depth(self, root):
        if root is None:
            return 0
        d = max(self.build_depth(root.left), self.build_depth(root.right)) + 1
        self.depth[root.val] = d
        return d

• 一次递归

class Solution:

    def lcaDeepestLeaves(self, root: TreeNode) -> TreeNode:
        return self.get_lca(root)[0]

    def get_lca(self, root: TreeNode) -> Tuple[TreeNode, int]:
        if root is None:
            return root, 0
        l_ret, l_dep = self.get_lca(root.left)
        r_ret, r_dep = self.get_lca(root.right)
        ans_dep = max(l_dep, r_dep) + 1
        if l_dep == r_dep:
            return root, ans_dep
        elif l_dep < r_dep:
            return r_ret, ans_dep
        else:
            return l_ret, ans_dep

1.10.2. BST的LCA

235. 二叉搜索树的最近公共祖先

面试题68 - I. 二叉搜索树的最近公共祖先（迭代 / 递归，清晰图解）

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        qv = q.val
        pv = p.val
        while root:
            rv = root.val
            if rv < qv and rv < pv:
                root = root.right
            elif rv > qv and rv > pv:
                root = root.left
            else:
                break
        return root

1.11 二叉树与链表

1.11.1 二叉树展开为链表

1.11.1.1 先序

114. 二叉树展开为链表

一、两阶段：中序遍历+展开链表 — 时间 $O(N)$ 空间 $O(N)$

class Solution:
    def flatten(self, root: TreeNode) -> None:
        preorderList = list()

        def preorderTraversal(root: TreeNode):
            if root:
                preorderList.append(root)
                preorderTraversal(root.left)
                preorderTraversal(root.right)
        
        preorderTraversal(root)
        size = len(preorderList)
        for i in range(1, size):
            prev, curr = preorderList[i - 1], preorderList[i]
            prev.left = None
            prev.right = curr

二、用栈遍历，同时更新prev结点实现【展开链表】
时间 $O(N)$ 空间 $O(N)$ — 空间复杂度来自【栈的空间】

只能用非递归

class Solution:
    def flatten(self, root: TreeNode) -> None:
        if not root: return
        stack = [root]
        prev = None
        while stack:
            curr = stack.pop()
            if prev:
                prev.left = None
                prev.right = curr
            left, right = curr.left, curr.right
            if right:
                stack.append(right)
            if left:
                stack.append(left)
            prev = curr

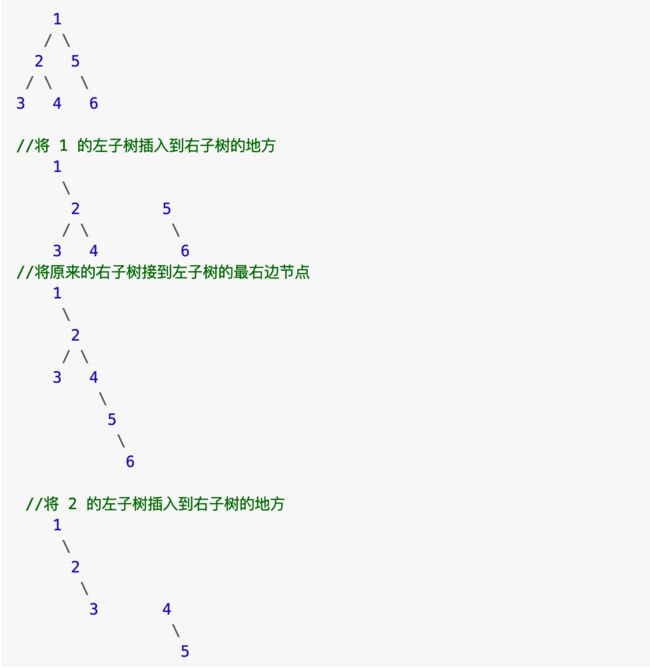
三、寻找前驱结点

详细通俗的思路分析，多解法

1. 将左子树插入到右子树的地方
2. 将原来的右子树接到左子树的最右边节点
3. 考虑新的右子树的根节点，一直重复上边的过程，直到新的右子树为 null

• 前序遍历

class Solution:
    def flatten(self, root: TreeNode) -> None:
        if not root:
            return None
        left, right = root.left, root.right
        root.left = None
        root.right = left
        p = root
        while p.right:
            p = p.right
        p.right = right
        self.flatten(root.right)

• 后序遍历

class Solution:
    def flatten(self, root: TreeNode) -> None:
        if not root:
            return None
        self.flatten(root.left)
        self.flatten(root.right)
        left, right = root.left, root.right
        root.left = None
        root.right = left
        p = root
        while p.right:
            p = p.right
        p.right = right

• 非递归，迭代

class Solution:
    def flatten(self, root: TreeNode) -> None:
        while root:
            left, right = root.left, root.right
            root.left = None
            root.right = left
            p = root
            while p.right:
                p = p.right
            p.right = right
            root = root.right

1.11.1.2 中序

897. 递增顺序搜索树

注意一个坑：

class Solution:
    def increasingBST(self, root: TreeNode) -> TreeNode:
        dummmy = TreeNode(-1)
        pre = dummmy

        def inorder(root):
            nonlocal pre
            if not root: return
            # left
            inorder(root.left)
            # travel
            if pre:
                # 不是 pre.left = None
                root.left = None
                pre.right = root
            pre = root
            # right
            inorder(root.right)

        inorder(root)
        return dummmy.right

1.11.2 二叉树展开为双向循环链表【中序】

剑指 Offer 36. 二叉搜索树与双向链表

面试题36. 二叉搜索树与双向链表（中序遍历，清晰图解）

• 递归

class Solution:
    def treeToDoublyList(self, root: 'Node') -> 'Node':
        if not root: # 记得处理边界条件
            return root

        pre = None
        head = None

        def travel(node: Node):
            nonlocal pre, head
            if node is None:
                return
            travel(node.left)
            if head is None:
                # 不设dummy head
                head = node
            if pre is not None:
                pre.right = node
            node.left = pre
            pre = node
            travel(node.right)

        travel(root)
        pre.right = head # 加了后两句就好了
        head.left = pre
        return head

• 非递归

class Solution:
    def treeToDoublyList(self, root: 'Node') -> 'Node':
        if not root: return None
        stack = []
        pre = None
        head = None
        while root or stack:
            while root:
                stack.append(root)
                root = root.left
            root = stack.pop()
            if root:
                if head is None:
                    head = root
                if pre is not None:
                    pre.right = root
                root.left = pre
                pre = root
                root = root.right
        pre.right = head
        head.left = pre
        return head

1.12 二叉树与回溯

1.12.1 不同的BST

给一个长度为$N$的有序序列$S$，问有多少种不同的BST树结构$\{T\}$，其中序遍历序列$S^{\prime }=S$ 。(1) 求不同的BST树结构数量$|T|$ 。 (2) 求BST树结构集合$\{T\}$

1. 如果直接问数量，直接答catalan数（见下文公式）。同理如果问进栈出栈形成某序列的问题解空间数量，也为catalan数。
2. 定义一个generate(start, end)函数，返回值为序列$S=[s\cdots e]$生成的BST树结构集合$\{T\}$。不妨对这个序列做一轮遍历（$i=s\cdots e$），用 $i$ 构造根节点，左侧序列$[s\cdots i-1]$形成一个集合$\{T_L\}$，右侧序列$[i+1\cdots e]$形成一个集合$\{T_R\}$，这两个集合做笛卡尔积，分别做根节点的左右子树。递归完成构造
   

96. 不同的二叉搜索树

catalan 数：

$$\frac{C_{2n}^n}{n+1}$$

def C(a, b):
    ans = 1
    for _ in range(b):
        ans *= a
        a -= 1
    while b >= 1:
        ans //= b
        b -= 1
    return ans

def catalan(n):
    return C(2*n, n) // (n + 1)


class Solution:
    def numTrees(self, n: int) -> int:
        return (catalan(n))

95. 不同的二叉搜索树 II

class Solution:
    def generateTrees(self, n: int) -> List[TreeNode]:
        def generate(start, end):
            if start > end:
                return [None, ]
            ans = []
            for i in range(start, end + 1):
                left_nodes = generate(start, i - 1)
                right_nodes = generate(i + 1, end)
                for left_node in left_nodes:
                    for right_node in right_nodes:
                        ans.append(TreeNode(i, left_node, right_node))
            return ans

        return generate(1, n)

1.12.2 所有可能的满二叉树

894. 所有可能的满二叉树

class Solution:
    memo = {0:[], 1:[TreeNode(0)]}
    def allPossibleFBT(self, n: int) -> List[TreeNode]:
        if n in self.memo:
            return self.memo[n]
        ans = []
        for x in range(n):
            y = n - 1 - x
            for left in self.allPossibleFBT(x):
                for right in self.allPossibleFBT(y):
                    root = TreeNode(0)
                    root.left = left
                    root.right = right
                    ans.append(root)
        self.memo[n] = ans
        return ans

1.12.3 二叉搜索树序列

面试题 04.09. 二叉搜索树序列

[二叉搜索树序列] 简洁递归 举例说明 Python

class Solution:
    def BSTSequences(self, root: TreeNode) -> List[List[int]]:
        if not root: return [[]]
        ans: List[List[int]] = []

        def dfs(root, choices, path):
            if root.left:
                choices.append(root.left)
            if root.right:
                choices.append(root.right)
            if not choices:
                ans.append(path)
            for i in range(len(choices)):
                dfs(choices[i], choices[:i] + choices[i + 1:], path + [choices[i].val])

        dfs(root, [], [root.val])
        return ans

2. 树与DP

2.1 打家劫舍

2.2 监控二叉树

968. 监控二叉树

[监控二叉树] 后序遍历递归状态 贪心决策 Python

NONE = 0
COVER = 1
CAMERA = 2
class Solution:
    def minCameraCover(self, root: TreeNode) -> int:
        self.res = 0
        def dfs(root):
            # 叶子结点默认为NONE
            if root is None:
                return COVER
            left = dfs(root.left)
            right = dfs(root.right)
            # 如果任一为【无覆盖】NONE，则应该为【摄像头】CAMERA
            if left == NONE or right == NONE:
                self.res += 1
                return CAMERA
            # 表面被子结点【覆盖】了
            if left == CAMERA or right == CAMERA:
                return COVER
             # 最经典的叶子结点为【无覆盖】NONE
            if left == COVER and right == COVER:
                return NONE
        if dfs(root) == NONE:
            self.res += 1
        return self.res