代码随想录算法训练营day17|Leetcode110/257/404
Leetcode257二叉树的所有路径
链接:257. 二叉树的所有路径 - 力扣(LeetCode)
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
思路: 递归+回溯法
这里有两种方法。第一: 两层for循环,分别遍历左子树和右子树。
特例:如果只有1个root,那么可以直接添加到结果集种[str(root)],注意在添加的过程中要对应上lettcode的输出要求,要加上‘->'并且把节点的值转换为字符
第二:
新构建一个函数分别对左右子树进行递归,但是用什么遍历方法呢?
答案是用前序遍历,中左右的遍历顺序去判断,那么递归的终止条件呢?也就是遍历到左右节点都为空的时候 停止递归 返回当前路径
首先,我们先将中间节点加入到path中,然后判断下面的左右孩子是否为空,如果不为空就开始递归。并且,递归完了之后别忘了需要回溯才可以!!!需要不断的删除节点,然后继续判断新的节点。所以 回溯和递归永远是一家
代码:
def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
#第一种
# result = []
# if not root:
# return []
# if not root.left and not root.right:
# return [str(root.val)]
# if root.left:
# for i in self.binaryTreePaths(root.left):
# result.append(str(root.val)+'->'+i)
# if root.right:
# for j in self.binaryTreePaths(root.right):
# result.append(str(root.val)+'->'+j)
# return result
----------------------------------
#第二种
path = ''
result = []
if not root: return result
self.traversal(root, path, result)
return result
##回溯算法+递归
def traversal(self,node:TreeNode,path,result):
path+=(str(node.val))
if not node.left and not node.right:
result.append(path)
if node.left:
self.traversal(node.left,path + '->',result)
if node.right:
self.traversal(node.right,path + '->',result)leetcode110平衡二叉树
链接:110. 平衡二叉树 - 力扣(LeetCode)
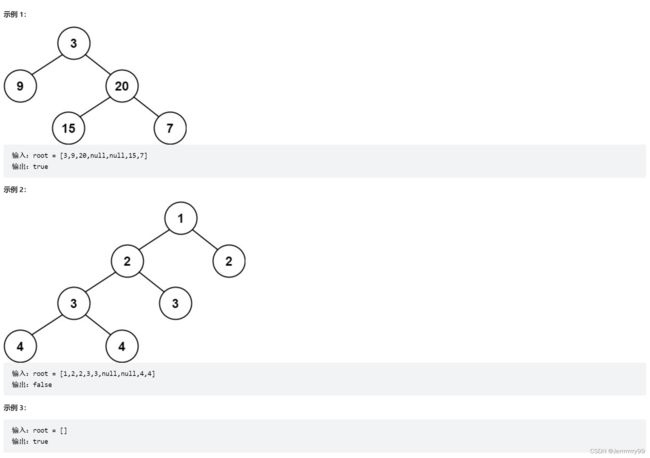
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
思路:判断子树是不是平衡二叉树
如果子树都不是平衡二叉树就可以直接返回-1给父节点
如果左右子树都是平衡二叉树 那么就两边取最大高度加上本身高度返回给父节点 最后判断是否等于-1也就是判断 是否为平衡二叉树
既然是求高度,那么就需要用后序遍历的方法
因为求深度可以从上到下去查 所以需要前序遍历(中左右),而高度只能从下到上去查,所以只能后序遍历(左右中)
如图所示:
递归三步曲分析:
- 明确递归函数的参数和返回值
参数:当前传入节点。
返回值:以当前传入节点为根节点的树的高度。
那么如何标记左右子树是否差值大于1呢?
如果当前传入节点为根节点的二叉树已经不是二叉平衡树了,还返回高度的话就没有意义了。
所以如果已经不是二叉平衡树了,可以返回-1 来标记已经不符合平衡树的规则了。
代码:
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
if self.get_height(root)==-1:
return False
else:
return True
def get_height(self,root):
if not root:
return 0
left_height = self.get_height(root.left)
if left_height==-1:
return -1
right_height = self.get_height(root.right)
if right_height==-1:
return -1
result = 0
if abs(left_height-right_height)<=1:
result=1+max(left_height,right_height)
else:
result=-1
return resultleetcode404左叶子之和
链接:404. 左叶子之和 - 力扣(LeetCode)
 首先这道题既然是左叶子之和,那么是不是首先要判断是否为叶子节点 ?
首先这道题既然是左叶子之和,那么是不是首先要判断是否为叶子节点 ?
那么如果说他是一个叶子节点 但是怎么得到他的左叶子呢?
首先要注意是判断左叶子,不是二叉树左侧节点,所以不要上来想着层序遍历。
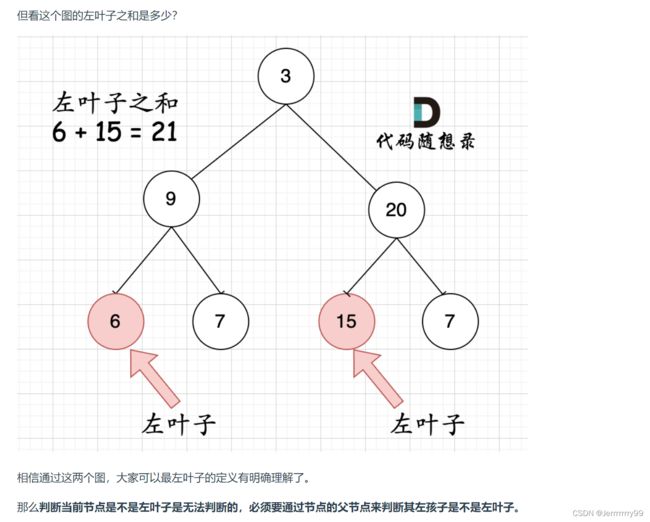
因为题目中其实没有说清楚左叶子究竟是什么节点,那么我来给出左叶子的明确定义:节点A的左孩子不为空,且左孩子的左右孩子都为空(说明是叶子节点),那么A节点的左孩子为左叶子节点
示例:
所以说 判断当前节点是不是左叶子 是要通过父节点来判断的
也就是 if root.left!=none and root.left.left==none and root.left.right==none
如果满足这个逻辑,那么当前节点就是左叶子节点
此时我们记录一下当前节点的值left_val = root.left.val
然后我们的右子树是不是也需要去判断左叶子节点!
直接递归right_val = self.sum(root.right)这里sum是我个人定义的函数名,大家随意
最后left+right得到他们的和
递归三部曲:
确定递归函数的参数和返回值
判断一个树的左叶子节点之和,那么一定要传入树的根节点,递归函数的返回值为数值之和,所以为int
使用题目中给出的函数就可以了。
确定终止条件
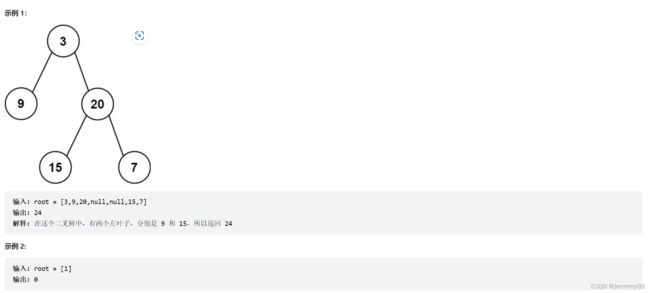
如果遍历到空节点,那么左叶子值一定是0(看上图案例1)
确定单层递归的逻辑
当遇到左叶子节点的时候,记录数值,
然后通过递归求取左子树左叶子之和,和 右子树左叶子之和,相加便是整个树的左叶子之和。
代码:
class Solution:
def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:
return self.sum(root)
def sum(self,root):
if not root:
return 0
if root.left==None and root.right==None:
return 0
left_val = self.sum(root.left)
if root.left!=None and root.left.left==None and root.left.right==None:
left_val = root.left.val
right_val = self.sum(root.right)
total = left_val + right_val
return total