435. 无重叠区间【贪心算法】
435. 无重叠区间
题目链接:https://leetcode-cn.com/problems/non-overlapping-intervals/
给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。
注意:
可以认为区间的终点总是大于它的起点。
区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。
示例 1:
输入: [ [1,2], [2,3], [3,4], [1,3] ]
输出: 1
解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例 2:
输入: [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:
输入: [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
思路:
相信很多同学看到这道题目都冥冥之中感觉要排序,但是究竟是按照右边界排序,还是按照左边界排序呢?
按照右边界排序,就要从左向右遍历,因为右边界越小越好,只要右边界越小,留给下一个区间的空间就越大,所以从左向右遍历,优先选右边界小的。
按照左边界排序,就要从右向左遍历,因为左边界数值越大越好(越靠右),这样就给前一个区间的空间就越大,所以可以从右向左遍历。
如果按照左边界排序,还从左向右遍历的话,其实也可以,逻辑会有所不同。
一些同学做这道题目可能真的去模拟去重复区间的行为,这是比较麻烦的,还要去删除区间。
题目只是要求移除区间的个数,其实没有必要去真实的模拟删除区间!
按照右边界排序,从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了。
此时问题就是要求非交叉区间的最大个数。
右边界排序之后,局部最优:优先选右边界小的区间,所以从左向右遍历,留给下一个区间的空间大一些,从而尽量避免交叉。全局最优:选取最多的非交叉区间。
局部最优推出全局最优,试试贪心!
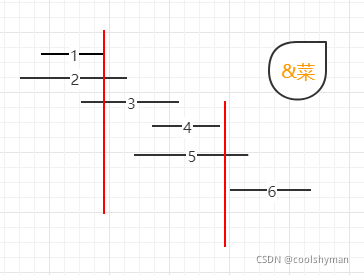
这里记录非交叉区间的个数还是有技巧的,如图:
区间,1,2,3,4,5,6都按照右边界排好序。
每次取非交叉区间的时候,都是可右边界最小的来做分割点(这样留给下一个区间的空间就越大),所以第一条分割线就是区间1结束的位置。
接下来就是找大于区间1结束位置的区间,是从区间4开始。那有同学问了为什么不从区间5开始?别忘已经是按照右边界排序的了。
区间4结束之后,在找到区间6,所以一共记录非交叉区间的个数是三个。
总共区间个数为6,减去非交叉区间的个数3。移除区间的最小数量就是3。
Java代码如下:
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
if (intervals.length < 2) return 0;
// 按照区间右边界排序
Arrays.sort(intervals, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
if (o1[1] != o2[1]) {
return Integer.compare(o1[1],o2[1]);
} else {
return Integer.compare(o1[0],o2[0]);
}
}
});
int count = 1;// intervals 不为空至少需要一支箭
int edge = intervals[0][1];
for (int i = 1; i < intervals.length; i++) {
if (edge <= intervals[i][0]){
count ++; // 需要一支箭
edge = intervals[i][1];// 更新重叠气球最小右边界
}
}
return intervals.length - count;
}
}
什么是贪心算法?
贪心的本质是选择每一个阶段的局部最优,从而达到全局最优。
举个例子:
假如钱包里有一堆钞票,你可以拿走5张,如果想要尽可能的拿到最大的金额,你要如何拿?
每次拿最大的,最终结果就是拿走最大的金额数。
每次拿最大的就是局部最优,最后拿走最大数额的钱就是推出全局最优。