【leetcode】floodfill算法
floodfill算法
- 一、图像渲染
-
- 1、题目描述
- 2、代码
- 3、解析
- 二、岛屿数量
-
- 1、题目描述
- 2、代码
- 3、解析
- 三、岛屿最大面积
-
- 1、题目描述
- 2、代码
- 3、解析
- 四、被围绕的区域
-
- 1、题目描述
- 2、代码
- 3、解析
- 五、太平洋大西洋水流问题
-
- 1、题目描述
- 2、代码
- 3、解析
- 六、扫雷游戏
-
- 1、题目描述
- 2、代码
- 3、解析
- 七、衣柜整理
-
- 1、题目描述
- 2、代码
- 3、解析
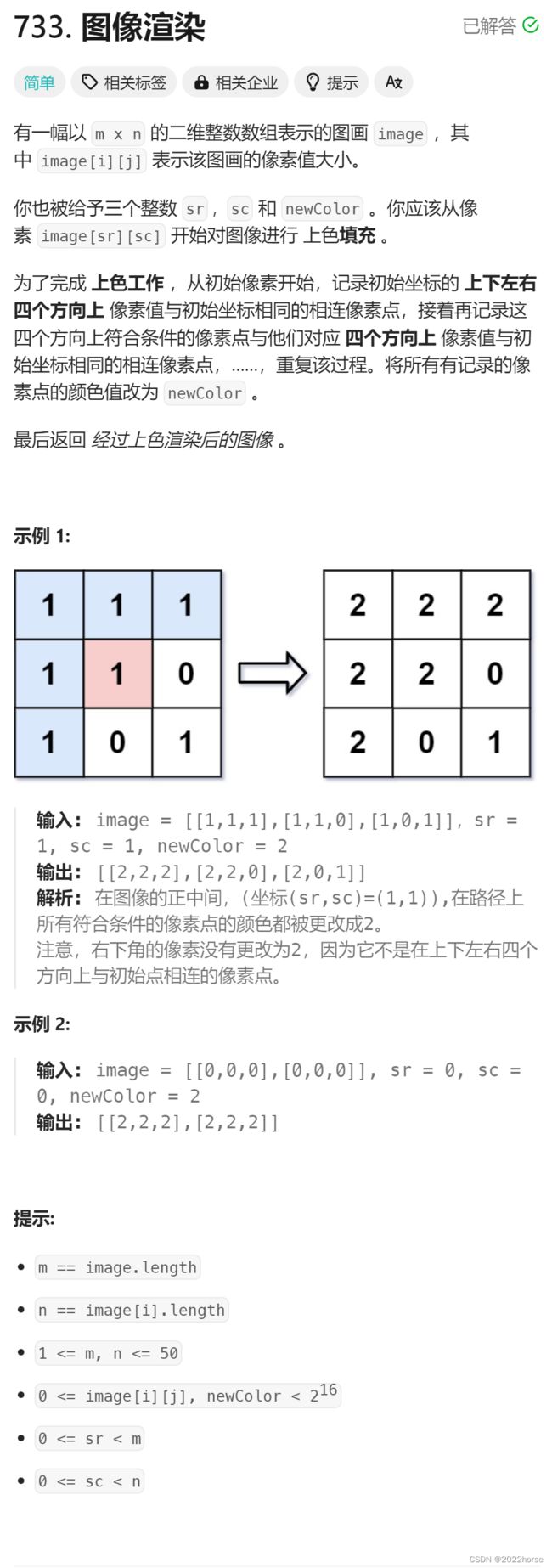
一、图像渲染
1、题目描述
2、代码
class Solution
{
public:
// 全局变量
int dx[4] = {0, 0, -1, 1};
int dy[4] = {1, -1, 0, 0};
int m, n;
int Init;
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color)
{
if(image[sr][sc] == color) // 相同数
{
return image;
}
m = image.size();
n = image[0].size();
Init = image[sr][sc]; // 刚开始的初识值
dfs(image, sr, sc, color);
return image;
}
void dfs(vector<vector<int>>& image, int i, int j, int color)
{
// 刚进来就进行改颜色
image[i][j] = color;
for(int k = 0; k < 4; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && Init == image[x][y])
{
dfs(image, x, y, color);
}
}
}
};
3、解析
从(sr,sc)位置开始,先将该位置值覆盖掉,然后进行上下左右的顺序走,遇见走不通的路就回溯,直到走到原位置就停下即可。
二、岛屿数量
1、题目描述
2、代码
class Solution
{
public:
// 全局变量
vector<vector<bool>> visit;
int m, n;
int ret; // 统计岛屿数量的
int numIslands(vector<vector<char>>& grid)
{
m = grid.size();
n = grid[0].size();
// 初始化visit数组
visit = vector<vector<bool>>(m, vector<bool>(n));
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(!visit[i][j] && grid[i][j] == '1')
{
ret++;
dfs(grid, i, j);
}
}
}
return ret;
}
// 上下左右移动
int dx[4] = {0, 0, -1, 1};
int dy[4] = {1, -1, 0, 0};
void dfs(vector<vector<char>>& grid, int i, int j)
{
// 标记当前坐标已经被访问过了
visit[i][j] = true;
for(int k = 0; k < 4; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && !visit[x][y] && grid[x][y] == '1')
{
dfs(grid, x, y);
}
}
}
};
3、解析
我们要明确一个点,是先要将该递归放在一个全局的视角去看待,并且要相信这个递归它是会自动回溯的,我们抱着这种想法来进行写下面的思路:
首先,我们先定义一个二维数组visit用来标记一下当前的位置是否被访问过,其次遍历这个二维数组,每遇到第一个1的时候先将数量进行加1,然后进入dfs深度优先遍历中,进入后,我们先定义其为true,也就是被访问过了,然后进行上下左右进行联通即可。
三、岛屿最大面积
1、题目描述
leetcode链接
2、代码
class Solution
{
public:
// 全局变量
vector<vector<bool>> visit;
int m, n;
int sum; // 统计最多数量
int count; // 统计每个1的数量
int maxAreaOfIsland(vector<vector<int>>& grid)
{
m = grid.size();
n = grid[0].size();
visit = vector<vector<bool>>(m, vector<bool>(n));
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(!visit[i][j] && grid[i][j] == 1)
{
count = 0; // 每次进来先更新一下为0
dfs(grid, i, j);
sum = max(count, sum); // 取最大值
}
}
}
return sum;
}
int dx[4] = {0, 0, -1, 1};
int dy[4] = {1, -1, 0, 0};
void dfs(vector<vector<int>>& grid, int i, int j)
{
visit[i][j] = true;
count++; // 这里每次进来都要进行++,因为要避免回溯的情况
for(int k = 0; k < 4; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && !visit[x][y] && grid[x][y] == 1)
{
dfs(grid, x, y);
}
}
}
};
3、解析
这道题的做法和上面一道题的基本框架一样的,无非就是每经过一个联通的岛屿其count都++,而这道题目必定是有诱惑人犯错的地方的,我在做这道题的时候其每次递归没有理解透彻导致只通过了部分样例,我们来分析一下我之前写的代码:

所以我们定一个全局的count变量,然后在每次进入1围成的岛屿中count都重新更新为0,然后再进入到dfs深度优先遍历函数进行递归,每次遇到一个1就++,并且进行标记当前位置被访问过了,剩下思路和上面一道题思路一样。
四、被围绕的区域
1、题目描述
2、代码
方法一:(用visit数组标记法)
class Solution
{
public:
// 全局变量
vector<vector<bool>> visit;
int m, n;
void solve(vector<vector<char>>& board)
{
m = board.size();
n = board[0].size();
visit = vector<vector<bool>>(m, vector<bool>(n));
// 横着的
for(int j = 0; j < n; j++)
{
if(!visit[0][j] && board[0][j] == 'O')
{
dfs(board, 0, j);
}
if(!visit[m - 1][j] && board[m - 1][j] == 'O')
{
dfs(board, m - 1, j);
}
}
// 竖着的
for(int i = 0; i < m; i++)
{
if(!visit[i][0] && board[i][0] == 'O')
{
dfs(board, i, 0);
}
if(!visit[i][n - 1] && board[i][n - 1] == 'O')
{
dfs(board, i, n - 1);
}
}
// 遍历整个
for(int i = 1; i < m - 1; i++)
{
for(int j = 1; j < n - 1; j++)
{
if(!visit[i][j] && board[i][j] == 'O')
{
DFS(board, i, j);
}
}
}
}
int dx[4] = {0, 0, -1, 1};
int dy[4] = {1, -1, 0, 0};
// 给竖着的定义true即可
void dfs(vector<vector<char>>& board, int i, int j)
{
visit[i][j] = true;
for(int k = 0; k < 4; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && !visit[x][y] && board[x][y] == 'O')
{
dfs(board, x, y);
}
}
}
// 整体给改成X
void DFS(vector<vector<char>>& board, int i, int j)
{
visit[i][j] = true;
board[i][j] = 'X';
for(int k = 0; k < 4; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && !visit[x][y] && board[x][y] == 'O')
{
DFS(board, x, y);
}
}
}
};
方法二(修改值法):
class Solution
{
public:
// 全局变量
int m, n;
void solve(vector<vector<char>>& board)
{
m = board.size();
n = board[0].size();
// 横着的
for(int j = 0; j < n; j++)
{
if(board[0][j] == 'O')
{
dfs(board, 0, j);
}
if(board[m - 1][j] == 'O')
{
dfs(board, m - 1, j);
}
}
// 竖着的
for(int i = 0; i < m; i++)
{
if(board[i][0] == 'O')
{
dfs(board, i, 0);
}
if(board[i][n - 1] == 'O')
{
dfs(board, i, n - 1);
}
}
// 遍历整个
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(board[i][j] == 'O')
{
board[i][j] = 'X';
}
if(board[i][j] == '.')
{
board[i][j] = 'O';
}
}
}
}
int dx[4] = {0, 0, -1, 1};
int dy[4] = {1, -1, 0, 0};
void dfs(vector<vector<char>>& board, int i, int j)
{
board[i][j] = '.';
for(int k = 0; k < 4; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'O')
{
dfs(board, x, y);
}
}
}
};
3、解析
方法一的解析就很复杂,是需要用两个递归函数的,先把四周的围墙中的‘O’字符给全部标记已经访问过,然后横坐标从1这个位置到m-1这个位置,纵坐标从1这个位置到n-1这个位置进行找’O’这个字符,找到就进入DFS深度游优先变量这个函数进行递归,联通区全部改成’X’即可。
方法二的解析比较简单,只需要用到一个递归函数,同样先把四周围墙中的’O’改成’.‘,然后再遍历整个数组,将’.‘改成’O’,将’O’改成’X’即可。
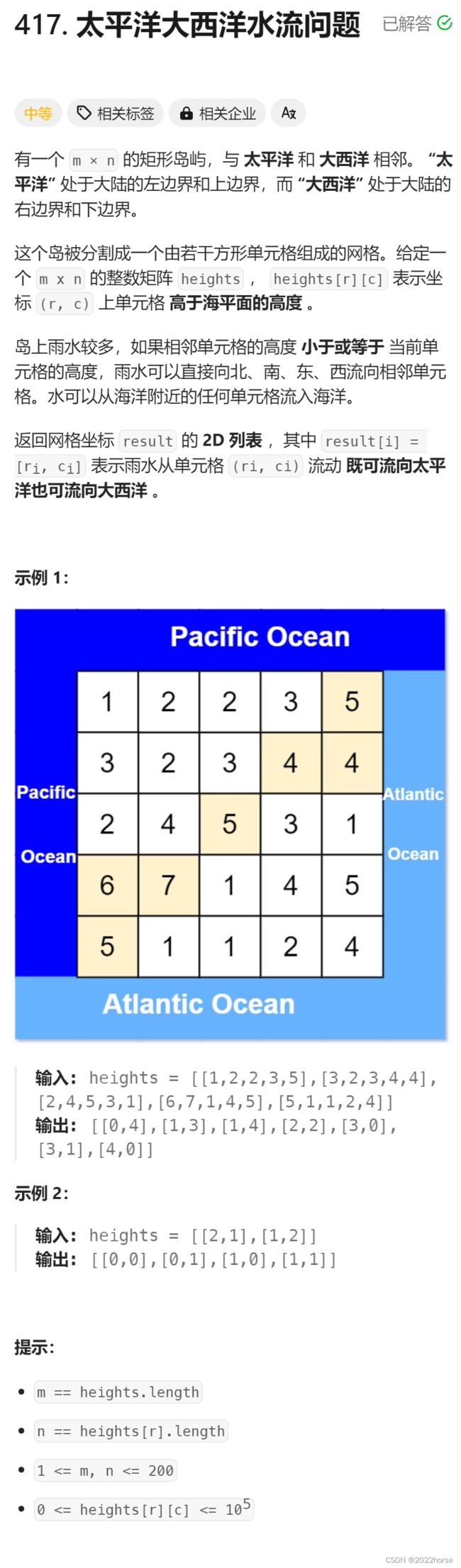
五、太平洋大西洋水流问题
1、题目描述
leetcode链接
2、代码
class Solution
{
public:
// 全局变量
int m, n;
int dx[4] = {0, 0, -1, 1};
int dy[4] = {1, -1, 0, 0};
vector<vector<int>> ret;
vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights)
{
m = heights.size();
n = heights[0].size();
vector<vector<bool>> pac(m, vector<bool>(n));
vector<vector<bool>> atl(m, vector<bool>(n));
// 第一行--与pac洋有关
for(int j = 0; j < n; j++)
{
dfs(heights, 0, j, pac);
}
// 第一列--与pac有关
for(int i = 0; i < m; i++)
{
dfs(heights, i, 0, pac);
}
// 最后一行--与atl有关
for(int j = 0; j < n; j++)
{
dfs(heights, m - 1, j, atl);
}
// 最后一列--与atl有关
for(int i = 0; i < m; i++)
{
dfs(heights, i, n - 1, atl);
}
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(pac[i][j] && atl[i][j])
ret.push_back({i, j});
}
}
return ret;
}
void dfs(vector<vector<int>>& heights, int i, int j, vector<vector<bool>>& path)
{
path[i][j] = true;
for(int k = 0; k < 4; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && !path[x][y] && heights[i][j] <= heights[x][y])
{
dfs(heights, x, y, path);
}
}
}
};
3、解析
我刚开始是用的是标记一个int类型的二维数组vector
六、扫雷游戏
1、题目描述
2、代码
class Solution
{
public:
// 全局变量
int dx[8] = {0, 0, -1, 1, 1, -1, -1, 1};
int dy[8] = {1, -1, 0, 0, 1, 1, -1, -1};
int m, n;
vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click)
{
m = board.size();
n = board[0].size();
int i = click[0]; // 横坐标
int j = click[1]; // 纵坐标
if(board[i][j] == 'M')
{
board[i][j] = 'X';
return board;
}
dfs(board, i, j);
return board;
}
void dfs(vector<vector<char>>& board, int i, int j)
{
// 统计一下周围雷的个数
int count = 0;
for(int k = 0; k < 8; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'M')
{
count++;
}
}
// 周围有雷
if(count)
{
board[i][j] = count + '0';
return;
}
else // 周围没雷
{
board[i][j] = 'B';
for(int k = 0; k < 8; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'E')
{
dfs(board, x, y);
}
}
}
}
};
3、解析
七、衣柜整理
1、题目描述
2、代码
class Solution
{
public:
// 全局变量
int dx[4] = {0, 0, -1, 1};
int dy[4] = {1, -1, 0, 0};
int sum;
bool visit[101][101];
int m, n, cnt;
int wardrobeFinishing(int _m, int _n, int _cnt)
{
m = _m;
n = _n;
cnt = _cnt;
dfs(0, 0, cnt);
return sum;
}
void dfs(int i, int j, int cnt)
{
sum++;
visit[i][j] = true;
for(int k = 0; k < 4; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && !visit[x][y] && check(x, y))
{
dfs(x, y, cnt);
}
}
}
bool check(int i, int j)
{
int tmp;
while(i)
{
tmp += i % 10;
i /= 10;
}
while(j)
{
tmp += j % 10;
j /= 10;
}
return tmp <= cnt;
}
};
3、解析
这道题目难度不大,但是最核心的问题是在于其是每个数位进行加减的,所以我们用到的是下面的将每一个数位进行加上的代码:

其余算法原理实在是太简单了,不详细赘述了,直接看代码即可。