Multiple View Geometry in Computer Vision Second Edition by Richard Hartley 读书笔记(二)
Chapter 2介绍的是2d下的投影变换,摘录下了以下定理
Result 2.1. The point x lies on the line l if and only if xTl = 0. (xTl = lTx = x.l )
Result 2.2. The intersection of two lines l and l′ is the point x = l × l′.
Result 2.4. The line through two points x and x′ is l = x × x′.
Result 2.6. Duality principle. To any theorem of 2-dimensional projective geometry there corresponds a dual theorem, which may be derived by interchanging the roles of points and lines in the original theorem. “点和直线在射影平面上的地位是对称的” 引述自《解析几何》丘维声。由之上3个定理也可以看出,两者可以直接交换得到另一个等式。它们互称为对偶命题4
Result2.7. The line l tangent to C at a point x on C is given by l=Cx.
Result2.13. Under a point transformation x′ = Hx, a conic C transforms to C′ = H−TCH−1.
Result 2.14. Under a point transformationx′ = Hx, a dual conic C∗ transforms toC∗′ = HC∗HT.
Result 2.16. The number of functionally independent invariants is equal to, or greater than, the number of degrees of freedom of the configuration less the number of degrees of freedom of the transformation.
Result 2.17. The line at infinity, l∞, is a fixed line under the projective transformation H if and only if H is an affinity.
Result 2.21. The circular points, I, J, are fixed points under the projective transformation H if and only if H is a similarity.
Result 2.22. The dual conic C∗∞ (a degenerate (rank 2) line conic C∗∞ = IJT + JIT )is fixed under the projective transformation H if and only if H is a similarity.
Result 2.23. Once the conic C∗∞ is identified on the projective plane then Euclidean angles may be measured by (2.22).
Result 2.24. Lines l and m are orthogonal if lTC∗∞m = 0.
Result 2.25. Once the conic C∗∞ is identified on the projective plane then projective distortion may be rectified up to a similarity.
Conic:
equation of a conic in homogeneous coordinates is \(ax^2 + bx + c = 0\)
in matrix form: \(x^TCx = 0\)
\[ C = \begin{bmatrix} a&b/2&d/2 \\ b/2&c&e/2 \\ d/2&e/2&f \end{bmatrix} \]
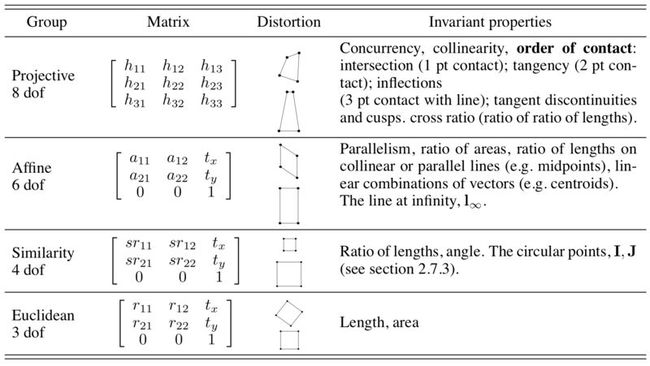
注意,这个矩阵是对称矩阵,且有6个参数,有1个用于缩放,那么就有5 degrees of freedom(这个概念后面也用得很多),因此5个点可以确定一个conic
A hierarchy of transformations:
应该是变换群的概念,例如“平面的所有正交变换组成的集合H是平面的一个变换群,称H为平面的正交变换群。”不过本书中提出 “An isometry is orientation-preserving if the upper left hand 2 × 2 matrix has determinant 1. Orientation-preserving isometries form a group, orientation-reversing ones do not. This distinction applies also in the case of similarity and affine transformations which now follow. ”朝向不变的才构成一个群,不知道为什么,待解决。
-
Isometries
\[ \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{bmatrix} \epsilon \cos \theta & -\sin\theta & t_x \\ \epsilon \cos \theta & \cos\theta & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \]
几何上的表现tx,ty是沿x轴、y轴的平移变换,R是旋转θ
它的Invariants 翻译过来应该是度量性质,包括length, angle, area
-
Similarity transformations
\[ \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{bmatrix} s \cos \theta & -s\sin\theta & t_x \\ s \cos \theta & s\cos\theta & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \]
增加了s,几何上表现是放缩
相似性质,高中学过,angle, ratio of two lengths,要注意以前提出的length就不是这里的invariants了
-
Affine transformations
\[ \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{bmatrix} a_{11} & a_{12} & t_x \\ a_{21} & a_{22} & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \]
几何上表现为沿某两垂直方向进行拉伸或压缩
仿射性质,包括Parallel lines, Ratio of lengths of parallel line segments, Ratio of areas.
Projective transformations
-
Projective transformations
\[ x' = H_Px = \begin{bmatrix} A & t \\ \nu^T & v \end{bmatrix} x \]
代数上表现为把无穷远线\( (0,0,1) \)
变换到一根普通直线\( (a,b,c) \),几何上表现为平行线于投影面上相交于一可见点(无穷远点)
射影性质,包括a ratio of ratios or cross ratio of lengths on a line , 即交比。注意并不是Ratio of lengths on a line(仿射性质)。
那么,一个投影变换就可以进行分解,如下图,我们需要什么样的性质,只需要退回到相应的变换之前。例如,如果想要测量投影图中的长度比,只需返回到相似变换。
\[ H = H_SH_AH_P = \begin{bmatrix} sR & t \\ 0^T & 1 \end{bmatrix} \begin{bmatrix} K & 0 \\ 0^T & 1 \end{bmatrix} \begin{bmatrix} I & 0 \\ \nu^T & v \end{bmatrix} = \begin{bmatrix} A & t \\ \nu^T & v \end{bmatrix} \]
各变换总结
2.5 接下来,书中从1D角度介绍了Cross Ratio、Concurrent lines。
2.6 以及1D、2D投影面的拓扑,完全没理解,,待补充。
2.7 介绍了如何从图像获取仿射、相似、度量性质
Metric rectification using \(C_*^∞\)
\begin{align*} {C_*^\infty}' & = (H_PH_AH_S)C_*^\infty(H_PH_AH_S)^T = (H_PH_A)C_*^\infty(H_SH_S^T)\\ & = (H_PH_A)C_*^\infty(H_SH_S^T) \\ & =\begin{bmatrix} KK_T & KK_T\nu \\ \nu^TKK_T & \nu^TKK_T\nu \end{bmatrix} \end{align*}
- 例1,把出现于图像中的无穷远线(2组平行线->两个无穷远点->确定无穷远线)投影回(0,0,1),就可以去除Projective Distortion。注意,一条直线有两个自由度,我们由Projective(8 def),Affine(6 def)之间的差也可以知道需要两个。
- 例2,已知length ratio,计算投影后的length ratio,1D坐标系,由length ratio得出 . homogeneous coordinates,再得出 H2*2,对应(1,0)的即为一个消失点。
- 例3,已知l的cross ratio,利用其得到一个相同投影中心下投影出的线,连线得出投影中心O,过O并与l平行的线交于无穷远点,经投影,此无穷远点(1,0)变换到(a,b),与l’交点即为无穷远点
- 例4,Projective Distortion已去除,由2 degrees of freedom of the circular points 去除Affine Distortion:垂线\( l′ T C_∗^∞ ′ m′ = 0 \),因为Projective Distortion已去除,v=0,那么 \[ \begin{pmatrix} l_1' & l_2' & l_3' \end{pmatrix} \begin{bmatrix} KK^T & 0 \\ 0^T & 0 \end{bmatrix} \begin{pmatrix} m_1' \\ m_2' \\ m_3' \end{pmatrix}=0 \] 两组垂线即可确定K:two such orthogonal line pairs provide two constraints which may be stacked to give a 2 × 3 matrix with s determined as the null vector ,rank为2,m为3,3-2=rank s,貌似,详见by Cholesky decomposition, section A4.2.1(p582) 也可以由以下确定:Alternatively, the two constraints required for metric rectification may be obtained from an imaged circle or two known length ratios. In the case of a circle, the image conic is an ellipse in the affinely rectified image, and the intersection of this ellipse with the (known) l∞ directly determines the imaged circular points.
- 例5,Projective Distortion未去除,仍由垂线\( l′ T C_∗^∞ ′ m′ = 0 \),公式\( (l^1m^1, (l^1m^2 + l^2m^1)/2, l^2m^2, (l^1m^3 + l^3m^1)/2, (l^2m^3 + l^3m^2)/2, l^3m^3) c = 0 \)矩阵形式1*6 6*1,类似例4,5个这样的限制形成5*6矩阵,c, and hence C∗∞, is obtained as the null vector.
注意,例5由一步直接到位,例4经过两步得到同样的效果,叫:This two-step approach is termed stratified
2.8 conics更多的性质
极点,极线,共轭
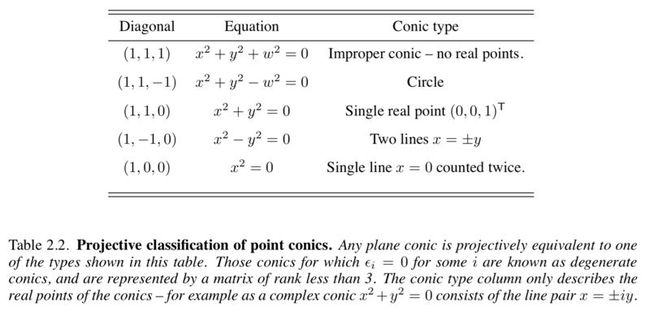
仿射、投影下对conics的分类:
投影变换下:any conic is equivalent under projective transforma- tion to one with a diagonal matrix. 证明过程见书
注意,仿射变换下:hyperbola, ellipse and parabola ,欧式分类也一样,因为只由他们与无穷远线的关系确定
2.9 固定的点和线,
由l∞ and the circular points ,可以发现有的点和线在一个投影变换下是固定的,实际上,矩阵的特征向量对应一个固定点,\( He = λe \) ,特征向量*特征值还是属于\( (x1,x2,x3) \),然后书中考察了相似矩阵(固定点即为circular points )、仿射矩阵的特征值和特征向量。