SGU 298. King Berl VI
SGU 298. King Berl VI
Memory limit: 65536 kilobytes
output: standard
King Berl VI has N daughters and no sons. During his long life he gave a number of promises to his daughters. All the promises have the following wording: "daughter Xi, I promise to give you dowry not less than Ci burles more than to daughter Yi", where i represents the number of the promise. Before his death the king decided to give some amount of money to each daughter. As far as he was the fair king, he decided to fullfill all his promises. But he was not only fair but also very greedy, he decided that he can give negative amount of burles as a dowry (i.e. daughter should pay this amount of burles to the treasury). Because of his born greed and by advice of the minister of finances, he made a decision that absolute value of each dowry should not exceed 10000 burles and the difference between dowry of the oldest and of the youngest daughters should be as small as possible (note, this value can be negative).
I.e. if the dowry given to the i-th daughter is Ai, folllowing conditions should be satisfied:
- -10000≤ Ai≤ 10000
- AN - A1 should be minimal
The fist line of the input file contains two integers numbers N and M (2≤ N≤ 10000; 0≤ M≤ 100000), where N is the number of daughters and M is the number of promises. The following M lines contain the description of promises in the following form: Xi, Yi, Ci (1≤ Xi, Yi≤ N; Xi≠ Yi; 0≤ Ci≤ 1000). The youngest daughter has the number one, the oldest — N. Each pair Xi, Yi can appear in the input several times.
Write to the output number -1 if there is no solution for the problem (i.e. there is no sequence of N integers which satisfies all described above requirements). Write to the output N integer numbers — the amount of dowry of each daughter in burles, if solution exists. If there are several solutions output any of them.
sample input |
sample output |
4 5 2 1 1 3 1 2 3 2 3 4 2 1 4 3 2 |
-3 -2 1 3 |
sample input |
sample output |
2 2 1 2 0 2 1 0 |
-7 -7 |
************************************************
题目大意:一个国王给他的n的女儿有m个承诺:a女儿的嫁妆比b女儿的嫁妆多c元或者等于c元。女儿的嫁妆可以是负数。一个女儿的嫁妆的绝对值比10000小。现在要求第n个女儿减去第1个女儿的值最小,求出序列。
解题思路:蛋疼地苦思冥想了2的成果也是对差分约束的深刻理解了吧:
差分约束系统
差分约束的一类求最大最小值,一般都说用最短路求最大值,用最长路求最小值。一种有点YY的证明,就拿最短路求最大值来说,一般最短路的时候初始值都是赋值为inf的,然后这个最短路不断更新也就是顶点的值不断减小,一旦更新到了最大一组解的时候,这个时候已经满足所有边的要求了,此时就不会再更新了,所以,最短路求出来的是最大解。比较YY的证明,总比没有好,就这样理解吧。
有一个定死的源点是有好处的。一个定死的源点的初始值是val,连到各个点的边的权值为0:
在用最短路求的时候,一开始所有点的初始值为inf,而最终求出的解是所有里面的最大值,并且,所有的值都比val小; 在用最长路求的时候,一开始所有的点初始值为-inf,而最终求出的解是所有里面的最小值,并且,所有的值都比val大。这样以来,如果一个差分约束系统的解有规定的上界uplim,我们可以外加一个源点,给它的初始值是uplim,然后从这个源点连到所有点的边权值为0,再用最短路求,求出的解的值必定比uplim小,而且是最大解,换句话说最靠近uplim的解。反之,如果一个差分约束系统的解有规定的下界downlim,我们可以外加一个源点,给它的初始值是downlim,然后从这个源点连到所有点的边权值为0,再用最长路求,求出的解的值必定比downlim大,而且是最小解,也就是最靠近downlim的解。
假设,一个差分约束系统有3个约束条件:a-b>=1,a-c>=2,c-b>=3,如果我们要求出a,b,c不比0大且最靠近0的那组解,我们就会建立如下的差分约束图:
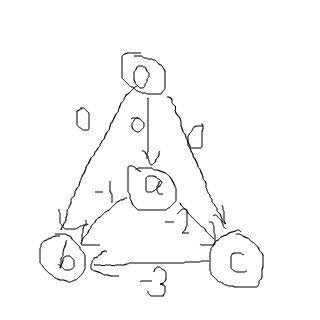
然后做最短路求最大解,求出了一组解{a,b,c}={0,-5,-2},但如果我们现在要求的是a,b,c都不比0大的且最靠近0的那组解,我们会建立这样的差分约束图:
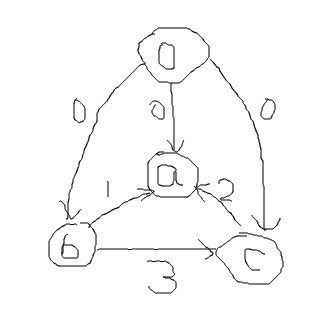
可见除了源点连出去的边不变外,其他边的方向取反,大小变成相反数。然后我们做最长路求最小解,可以得到{a,b,c}={5,0,3},有点觉得怪异了:上面两组解的结构是一样的,他们互相之间都只差了一个常数。然而,这个不是偶然,可以小证明一下:一个差分约束系统,先不考虑源点的问题,如果a有一条路径L连到b,这个路径是从a到b的最短路,a还可以通过其他途径连到b,那么当所有边都取反,权值也取相反数,从b到a通过路径L一定是最长路。那么换句话说也就是a一开始被什么东西制约,他后来还是被那个东西制约。所以第一次用正向边正权(这个正权的含义是相对与权值取相反数之后的反权来说的)做最短路求出来解一定和第二次用反向边反权做最长路求出来的解一定是结构相同都只是差了一个k的值。这个结论的意义是:如果差分约束的点的被限定了上下界,我们可以用一次最短路一次最长路来算出的最靠近上界的一组解和最靠近下界的一组解结构相同,然后,所有的解取值范围就一定在这两个解的值之间,不可能出现有一个解中一个点的取值超过这两组解的范围的。
还有一个连等式:(规定求最短路的那个图为正向边和正权)正向边正权最短路的解的结构=反向边反权最长路解的结构=正向边反权最长路解的值取相反数之后的结构=反向边正权最短路解的值取相反数之后的结构。前两个已经证明,第一个和第三个也很好证明:原来的最短路,取了相反数之后肯定变成最长路了,然而值也变成了相反数关系。并且,第一个和第三个的解是相反数,第二个和第四个解是相反数。
在一个差分约束系统中,如果之前已经做完最短路,现在把一个解xi给人为地缩小,然后再重新做最短路,这个是可以的。因为xi缩小,那么所有指向vi的边都还是能满足dis[v]<=dis[u]+cost的,但是vi出去的边就不能满足上面那个不等式了,然后,重新spfa能更新vi点以后的所有满足的点。但是如果做完最短路后把一个点人为扩大,我觉得这是不允许的,因为所有指向vi的边就不满足不等式了,重新spfa 的话应该不会有任何结果,因为vi指出去的边都满足,而指进来的边不会更新到,这样就搞笑了。与此同理,做完最长路后,我们可以把一个点人为地放大,然后spfa,但是不能缩小。
下面贴代码(研究透了_LT_zyc的代码http://hi.baidu.com/_lt_zyc/item/554a4f1979f311536826bb53):
//#pragma comment(linker, "/STACK:65536000")
#include <map>
#include <stack>
#include <queue>
#include <math.h>
#include <vector>
#include <string>
#include <fstream>
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>
#define N 10005
#define M 200005
#define E
#define inf 0x3f3f3f3f
#define dinf 1e10
#define linf (LL)1<<60
#define LL long long
#define clr(a,b) memset(a,b,sizeof(a))
using namespace std;
const int lim = 10000;
int n,m,eid;
int head[N],ed[M],nxt[M],val[M];
int x[M],y[M],v[M];
int d1[N],d2[N],vis[N],num[N];
queue<int>que;
void addedge(int s,int e,int v)
{
ed[eid]=e;val[eid]=v;
nxt[eid]=head[s];head[s]=eid++;
}
int spfa(int d[])
{
while(!que.empty())
{
int s=que.front();que.pop();
vis[s]=0;
for(int i=head[s];~i;i=nxt[i])
{
int e=ed[i],v=val[i];
if(d[e]>d[s]+v)
{
d[e]=d[s]+v;
if(!vis[e])
{
if(num[e]>n)return -1;
num[e]++;vis[e]=1;
que.push(e);
}
}
}
}
return 1;
}
int main()
{
//freopen("/home/axorb/in","r",stdin);
scanf("%d%d",&n,&m);
for(int i=0;i<m;i++)
scanf("%d%d%d",&x[i],&y[i],&v[i]);
eid=0;clr(head,-1);
for(int i=0;i<m;i++)addedge(x[i],y[i],-v[i]);
clr(vis,0);clr(num,0);
while(!que.empty())que.pop();
for(int i=1;i<=n;i++){d1[i]=0;que.push(i);}
int k=spfa(d1);
if(k==-1){puts("-1");return 0;}
for(int i=1;i<=n;i++)d1[i]+=lim;
eid=0;clr(head,-1);
for(int i=0;i<m;i++)addedge(y[i],x[i],-v[i]);
clr(vis,0);clr(num,0);
while(!que.empty())que.pop();
for(int i=1;i<=n;i++){d2[i]=0;que.push(i);}
k=spfa(d2);
if(k==-1){puts("-1");return 0;}
for(int i=1;i<=n;i++)d2[i]=-d2[i]-lim;
// for(int i=1;i<=n;i++)
// printf("%d: %d %d\n",i,d1[i],d2[i]);
for(int i=1;i<=n;i++)
if(d2[i]>d1[i]){puts("-1");return 0;}
eid=0;clr(head,-1);
for(int i=0;i<m;i++)addedge(x[i],y[i],-v[i]);
clr(vis,0);clr(num,0);
while(!que.empty())que.pop();
d1[n]=d2[n];que.push(n);
spfa(d1);
for(int i=1;i<=n;i++)
if(i==n)printf("%d\n",d1[i]);
else printf("%d ",d1[i]);
return 0;
}