【8086汇编基础】00--基础知识--各种进制的数据

基础知识

---

什么是进制？ 

对于同一个数字有很多表示方式。很久很久以前人们用棍子

计数，后来学会在地上画棍子，最终画在纸上．比如：

｜｜｜｜｜（５根棍子）

罗马人使用不同的符号表示棍子数目：｜｜｜仍然表示３根

棍子，而用V表示５根棍子用X表示１０根～

在当时，使用棍子计数是伟大的发明．用符号代替棍子更是

如此．如今采用十进制系统表示数字是最好的方法之一．之所以

这样说是因为它实现了用符号表示＂没有＂这一重要思想（３个XX?）

１５００年前的印度，零（０）第一次被看作一个数字．

稍后，这一概念在中东阿拉伯地区使用，最终传播到西方拉美国家。

在下面的学习中，你会逐渐认识到这个思想对于现代数字系统是多么

重要。

---

十进制系统

目前使用最多的是十进制．十进制系统有１０个数字

０，１，２，３，４，５，６，７，８，９

利用这些数字能表示任何数值，例如

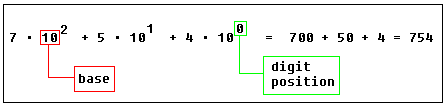
７５４

这些数字是由每一位数字乘以“基数”的幂累加而成的

（上一个例子中基数是10 因为十进制中有十个数字）。

 

位置对于每一个数字是很重要的。例如，你将上一个例子

中的“7”放到结尾：547

数值就成为：

 

特别提醒：任何数字的0次幂都是1，0的0次幂也是1

 

---

二进制

计算机没有人类聪明（至少现在是这样），制造一个只有

开关或者称为 0，1 两种状态的电子机器很容易。计算机

使用二进制系统，只有两个数字 

0, 1

基地为2

每一位二进制数称作一位（BIT），4 BIT 组成一个半字节（NIBBLE），

8BIT组成一个字节（BYTE），两个字节组成一个字（WORD），两个字

组成一个双字（DOUBLE WORD）（很少使用）：

 

习惯上在一串二进制后面加上“b”，这样，我们可以知道101b是二进制

表示十进制的5。

二进制10100101b表示十进制的165，计算方法如下：

 

---

十六进制系统

十六进制系统使用16个数字

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

基底是 16. 

十六进制非常紧凑，便于阅读。将二进制转换为十六进制

很容易，半字节（4bits） 对应一位十六进制如下表

 

Decimal (base 10) Binary (base 2) Hexadecimal (base 16) 0 0000 0 1 0001 1 2 0010 2 3 0011 3 4 0100 4 5 0101 5 6 0110 6 7 0111 7 8 1000 8 9 1001 9 10 1010 A 11 1011 B 12 1100 C 13 1101 D 14 1110 E 15 1111 F

习惯上我们在一个十六进制数的后面加上 "h"，以便和其他进制区别, 这样我们就知道 5Fh是一个十六进制数表示十进制的  95。习惯上，我们也在以字母开头（从Ａ到Ｆ）的十六进制数前面

加上"0"　例如： 0E120h. 

十六进制 1234h  等于　4660:

 

---

十进制到另外进制的换算 

在换算中，将十进制数不断除以目标进制的基底，每一次都要记录下商和余数，直到商０。

余数用来表示结果。


下面是一个十进制３９（基底是１０）到十六进制（基底是１６）的换算：

 
　

结果为　27h.
上例中所有的余数都小于１０，不必使用字母。

再举一个更复杂的例子：
十进制 43868 换算为十六进制：

 

结果是 0AB5Ch, 使用 上面提到的表 将大于９的数字替换成字母。 
　

运用同样的原理，我们可以换算为二进制（用２作除数），或者是先换算成十六进制，再用

上面的表　换算成二进制：

 

于是，得到二进制： 1010101101011100b 

---

有符号数 
　

对于十六进制数　0FFh　无法确定它是正数还是负数，因为它可以表示十进制的"255"

或者　 "- 1"。
８位可以表示２５６个状态，于是，我们可以假定前１２８个表示正数(从0到127)，接

下来的１２８个数(从128到256)表示负数 。

如果想表示"- 5"，我们从２５６中减去５，即　 256 - 5 = 251。
用这种复杂的方法表示一个负数有着数学依据的，数学上"- 5" 加上 "5"等于０。
当我们将两个８位的数字　5 和　251相加时，结果超过２５５，溢出处理为０！

 
　

128到256高位始终是１，这个可以作为数字符号的标记
对于字（１６位），１６位有65536个状态，头３２７６８个状态(从0到32767)用来

表示正数，下面的３２７６８个状态(从32767到65535) 表示负数。

　

---

Emu8086　带有数制转换工具，也可以计算各种数值表达式。选择菜单 Math 项: 

 

Number Convertor （数制转换）可以实现任意数制之间的转换。在文本框中填写源

数值，将自动转换到任意的数制。 可以作 8 位 或者 16 位转换。

Expression Evaluator（表达式计算）可以用来计算不同数制的计算以及从一个进制

到另一个进制的转换。输入表达式，按下回车，结果就会以你选定的进制表示。最长可以

进行３２位的计算。当在Signed打钩选中时（除了八进制和双字），最前面的一位将被认

作是符号位。这样以来，0FFFFFFFFh　将被认为是十进制的　－１。

例如，你计算　0FFFFh * 10h + 0FFFFh ( 8086 CPU所能访问的最大内存地址)。如果你选中

Signed 和 Word　选项，结果是　-17　（因为表达式被认为是　(-1) * 16 + (-1) ）。如果

想按照无符号数计算，请不要选择　Signed　表达式为　65535 * 16 + 65535　计算结果将是

1114095
同样你可以使用Number Convertor将非十进制换算为有符号的十进制，然后根据十进制

计算。

支持如下运算:

~       not　 (inverts all bits).
*       multiply.
/       divide.
%       modulus.
+       sum.
-       subtract (and unary -).
<<      shift left.
>>      shift right.
&       bitwise AND.
^       bitwise XOR.
|       bitwise OR.

二进制必须有“ｂ”作结尾，例如

00011011b
　

十六进制必须有"h"作结尾，另外，当地一位是字母时，最前面必须加上０，例如：

0ABCDh
八进制必须有"o"作结尾，例如：

77o

 

>>> 下一部分 >>>【8086汇编基础】01--汇编语言简要介绍