最短路/sgu 103 Traffic Lights

题意

    给出一个N个结点的无向图，每条边都有一个长度，但是每条边的两端有信号灯。信号灯有两种颜色：蓝色和紫色，并且信号灯有颜色变化的周期。当要走这条路，这条路的两端颜色一样时，才可以走，否则需要等到其中一个等变色后再走（走这条路的中途不用管灯的颜色）。给定两个点st,ed，求从st到ed最少的时间是多少。

 

输入：给出的灯的信息：C R Tb Tp。C表示开始时这个路口的灯的颜色，R表示当前这个颜色还要持续多久才会变成另一个颜色（为了方便描述，在后文记作“预热期”）。Tb表示这个路口的灯持续蓝色持续Tb，Tp同理。其实就是刚开始这个路口的颜色C会持续R秒，之后就开始有周期性的颜色交替了。

输出：最短时间 以及所经过的路口

 

分析

    就是求一个有条件限制的最短路。

    当对这条边进行松弛操作时，要算上等待到两端路口信号灯一致的时间所在的时刻，再加上这条路的长度。

    这样，问题的主体就分析清楚了。但是需要处理的是到某个路口需要等多久才可以通过这条边。

    我们记蓝色B为0，紫色P为1，t[i,0]存储的是B的周期，t[i,1]存储的是P的周期。

 

    构造一个函数calctime，表示想要通过这条边，在这个路口需要等待的时间，先来看一下这个函数：

 1 int calctime(int a,int b,int time,int f)

 2 {

 3     int ca,cb,ta,tb;

 4     color(a,time,ca,ta);color(b,time,cb,tb);

 5     if (ca==cb) return time;

 6     if (ta==tb)

 7     {

 8         if (f==0) {return calctime(a,b,ta,1);}

 9         else if (time<=r[a]||time<=r[b]) return calctime(a,b,ta,1);

10         else return INF;

11     }

12     return cmin(ta,tb);

13 }

 

其中，color(a,time,var ca,ta)表示在time时刻，a这个灯的颜色为ca，变成下一个颜色的时间点为ta。

显然，当a的颜色和b的颜色在time时刻相同时，即ca=cb时，不需要等待，直接返回当前时间点。

否则，当ca不等于cb时，我们需要等待其中一个灯变色，当ta不等于tb时，只需要返回其中较小的一个即可。

 

但是这题麻烦在，如果ca不等于cb，而ta=tb，即这两个灯当前颜色不一样，可是变成下一个颜色又在相同的时间时，该如何处理呢？

很显然，当这两个灯来来回回反复都是这样的话，说明这两个灯变色周期相同，则这两个灯永远达不到同时相等的时候，就是所谓的交替闪烁，成对称了。这条路不能通过。

但是，在ca不等于cb，ta=tb时，还有一种情况就是，其中一个或两个灯还在前面的“预热”状态，没有进入完整的循环周期，那么很有可能出现这种情况，但是这条路再等等还是可以通过的。

那么怎么判断呢？

 

很简单，当遇到需要等待的时间一样时，只需要再向下算一层。如果仍需要同样的时间，那么就成了“交替闪烁”了。否则，则是可以通过的。

至于实现，可以在calctime中再传递一个参数f,从主程序中传过去的f为0，表示第一次算，如果需要继续再算一层，则再函数中传递过去1，表示要计算下一层了。如果在计算第二层时，当前时间time在其中一个“预热”时间中，则说明这条路还有可能通过，否则这条路为对称的“交替闪烁”，永远过不去，返回一个最大值即可。

 

说完了calctime的实现，要具体说说color这个函数，即如何求解当前颜色以及变成下一个颜色的时间，先看看这个函数：

 1 void color(int a,int time,int& ca,int& ta)

 2 {

 3     if (time<r[a]) {ta=r[a];ca=c[a];return;}

 4     else 

 5     {

 6         int temp=(time-r[a])%(t[a][0]+t[a][1]);

 7         int now=time-temp;

 8         if (c[a]==1)

 9         {

10             if (temp<t[a][0]) {ca=0;ta=now+t[a][0];return;}

11                      else {ca=1;ta=now+t[a][0]+t[a][1];return;}

12         }

13         else 

14         {

15             if (temp<t[a][1]) {ca=1;ta=now+t[a][1];return;}

16                      else {ca=0;ta=now+t[a][0]+t[a][1];return;}

17         }

18     }

19 }

 

很显然，当前时间time在“预热”时间内时，颜色未改变，为初始颜色，则这个灯变色的时刻即为r时刻；

否则，记录一个temp，表示当前在整个循环周期的哪一位置

如果初始颜色为P,则：

1、如果temp<Tb(B的循环周期)，则当前颜色为B，且下一个变色时刻为time-temp+Tb的循环周期.如图：

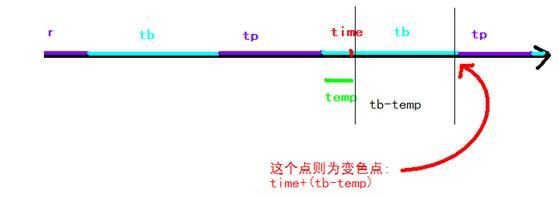
2、如果temp超过了tb，则说明在紫色范围内，下一个变色点即为time+tb+tp-temp；

如果初始颜色为B，则同理。

 

主要的函数构造完毕，只剩下spfa来打个酱油，很好写，只是要注意再开个数组记录一下路径

注意事项 无解时输出0

 

至此，整道题可以解决了。

 

Accepted Code

 

  1 /*

  2     PROBLEM:sgu103

  3     AUTHER:Rinyo

  4     MEMO:最短路

  5 */

  6 

  7 #include<cstdio>

  8 #include<cstring>

  9 

 10 int n,m,st,ed,INF;

 11 int r[310],c[310],ans[310],dist[310],last[310];

 12 int t[310][2];

 13 int map[310][310];

 14 bool v[310];

 15 int q[30010];

 16 

 17 inline int cmin(const int &x,const int &y) {return x<y?x:y;}

 18 

 19 void init()

 20 {

 21     scanf("%d%d%d%d",&st,&ed,&n,&m);

 22     for (int i=1;i<=n;i++)

 23     {

 24         char ch[5];

 25         scanf("%s%d%d%d",ch,&r[i],&t[i][0],&t[i][1]);

 26         if (ch[0]=='B') c[i]=0;else c[i]=1;

 27     }

 28     for (int i=1;i<=m;i++)

 29     {

 30         int x,y,z;

 31         scanf("%d%d%d",&x,&y,&z);

 32         map[x][y]=z;map[y][x]=z;

 33     }

 34 }

 35 

 36 void color(int a,int time,int& ca,int& ta)

 37 {

 38     if (time<r[a]) {ta=r[a];ca=c[a];return;}

 39     else 

 40     {

 41         int temp=(time-r[a])%(t[a][0]+t[a][1]);

 42         int now=time-temp;

 43         if (c[a]==1)

 44         {

 45             if (temp<t[a][0]) {ca=0;ta=now+t[a][0];return;}

 46                      else {ca=1;ta=now+t[a][0]+t[a][1];return;}

 47         }

 48         else 

 49         {

 50             if (temp<t[a][1]) {ca=1;ta=now+t[a][1];return;}

 51                      else {ca=0;ta=now+t[a][0]+t[a][1];return;}

 52         }

 53     }

 54 }

 55 

 56 int calctime(int a,int b,int time,int f)

 57 {

 58     int ca,cb,ta,tb;

 59     color(a,time,ca,ta);color(b,time,cb,tb);

 60     if (ca==cb) return time;

 61     if (ta==tb)

 62     {

 63         if (f==0) {return calctime(a,b,ta,1);}

 64         else if (time<=r[a]||time<=r[b]) return calctime(a,b,ta,1);

 65         else return INF;

 66     }

 67     return cmin(ta,tb);

 68 }

 69 

 70 void spfa()

 71 {

 72     memset(v,false,sizeof(v));

 73     for (int i=1;i<=n;i++) dist[i]=INF;

 74     int head=0,tail=1;

 75     v[st]=true;q[1]=st;dist[st]=0;last[st]=0;

 76     while (head<tail)

 77     {

 78         head++;

 79         int now=q[head];

 80         for (int i=1;i<=n;i++)

 81         {

 82             if (map[now][i]>0) 

 83             {

 84                 int temp=calctime(now,i,dist[now],0);

 85                 if (temp>=INF) continue;

 86                 if (temp+map[now][i]<dist[i])

 87                 {

 88                     dist[i]=temp+map[now][i];

 89                     last[i]=now;

 90                     if (!v[i]) {tail++;q[tail]=i;v[i]=true;}

 91                 }

 92             }

 93         }

 94         v[q[head]]=false;

 95     }

 96     if (dist[ed]>=INF) {printf("0");return;}

 97     printf("%d\n",dist[ed]);

 98     int now=ed,len=0;

 99     while (now!=0) {len++;ans[len]=now;now=last[now];}

100     for (int i=len;i>=2;i--) printf("%d ",ans[i]);

101     printf("%d\n",ans[1]);

102     return;

103 }

104 int main()

105 {

106     freopen("sgu103.in","r",stdin);

107     freopen("sgu103.out","w",stdout);

108     INF=99999999;

109     init();

110     spfa();

111     return 0;

112 }