2014年亚洲区域赛北京赛区现场赛A,D,H,I,K题解(hdu5112,5115,5119,5220,5122)
转载请注明出处: http://www.cnblogs.com/fraud/ ——by fraud
下午在HDU上打了一下今年北京区域赛的重现,过了5题,看来单挑只能拿拿铜牌,呜呜。
先将这五题的题解放上来,剩余题目等搞出来再补上
A题
A Curious Matt
Time Limit: 2000/2000 MS (Java/Others) Memory Limit: 512000/512000 K (Java/Others)
One day, Matt's best friend Ted is wandering on the non-negative half of the number line. Matt finds it interesting to know the maximal speed Ted may reach. In order to do so, Matt takes records of Ted’s position. Now Matt has a great deal of records. Please help him to find out the maximal speed Ted may reach, assuming Ted moves with a constant speed between two consecutive records.
For each test case, the first line contains an integer N (2 ≤ N ≤ 10000),indicating the number of records.
Each of the following N lines contains two integers t i and x i (0 ≤ t i, x i ≤ 10 6), indicating the time when this record is taken and Ted’s corresponding position. Note that records may be unsorted by time. It’s guaranteed that all t i would be distinct.
题目要求求出最大的速度
分析:以时间为key值,排序,然后遍历一遍

1 #include <iostream> 2 #include <cstring> 3 #include <iomanip> 4 #include <cmath> 5 #include <algorithm> 6 using namespace std; 7 int a[10010]; 8 int b[10010]; 9 double c[10010]; 10 int id[10010]; 11 bool cmp(int x,int y) 12 { 13 return a[x]<=a[y]; 14 } 15 int main() 16 { 17 ios::sync_with_stdio(false); 18 int t; 19 int n; 20 int cas=1; 21 cin>>t; 22 while(t--) 23 { 24 cin>>n; 25 a[0]=0,b[0]=0; 26 for(int i=0;i<n;i++) 27 { 28 cin>>a[i]>>b[i]; 29 id[i]=i; 30 } 31 sort(id,id+n,cmp); 32 double maxx=0; 33 for(int i=1;i<n;i++) 34 { 35 maxx=max(maxx,fabs((b[id[i]]-b[id[i-1]])*1.0/((a[id[i]]-a[id[i-1]])*1.0))); 36 } 37 cout<<"Case #"<<cas++<<": "; 38 cout<<fixed<<setprecision(2)<<maxx<<endl; 39 } 40 return 0; 41 }
D题
Dire Wolf
Time Limit: 5000/5000 MS (Java/Others) Memory Limit: 512000/512000 K (Java/Others)
Dire wolves look like normal wolves, but these creatures are of nearly twice the size. These powerful beasts, 8 - 9 feet long and weighing 600 - 800 pounds, are the most well-known orc mounts. As tall as a man, these great wolves have long tusked jaws that look like they could snap an iron bar. They have burning red eyes. Dire wolves are mottled gray or black in color. Dire wolves thrive in the northern regions of Kalimdor and in Mulgore.
Dire wolves are efficient pack hunters that kill anything they catch. They prefer to attack in packs, surrounding and flanking a foe when they can.
— Wowpedia, Your wiki guide to the World of Warcra
Matt, an adventurer from the Eastern Kingdoms, meets a pack of dire wolves. There are N wolves standing in a row (numbered with 1 to N from left to right). Matt has to defeat all of them to survive.
Once Matt defeats a dire wolf, he will take some damage which is equal to the wolf’s current attack. As gregarious beasts, each dire wolf i can increase its adjacent wolves’ attack by b i. Thus, each dire wolf i’s current attack consists of two parts, its basic attack ai and the extra attack provided by the current adjacent wolves. The increase of attack is temporary. Once a wolf is defeated, its adjacent wolves will no longer get extra attack from it. However, these two wolves (if exist) will become adjacent to each other now.
For example, suppose there are 3 dire wolves standing in a row, whose basic attacks ai are (3, 5, 7), respectively. The extra attacks b i they can provide are (8, 2, 0). Thus, the current attacks of them are (5, 13, 9). If Matt defeats the second wolf first, he will get 13 points of damage and the alive wolves’ current attacks become (3, 15).
As an alert and resourceful adventurer, Matt can decide the order of the dire wolves he defeats. Therefore, he wants to know the least damage he has to take to defeat all the wolves.
The second line contains N integers a i (0 ≤ a i ≤ 100000), denoting the basic attack of each dire wolf.
The third line contains N integers b i (0 ≤ b i ≤ 50000), denoting the extra attack each dire wolf can provide.

1 #include <iostream> 2 #include <cstring> 3 #include <cstdio> 4 using namespace std; 5 int a[310],b[310]; 6 int dp[310][310]; 7 int main() 8 { 9 ios::sync_with_stdio(false); 10 int t,n; 11 cin>>t; 12 int cas=1; 13 while(t--) 14 { 15 cin>>n; 16 for(int i=1;i<=n;i++)cin>>a[i]; 17 for(int i=1;i<=n;i++)cin>>b[i]; 18 b[0]=b[n+1]=0; 19 for(int p=0;p<n;p++) 20 { 21 for(int i=1;i<=n;i++) 22 { 23 int j=i+p; 24 if(i==j) 25 { 26 dp[i][j]=a[i]+b[i-1]+b[i+1]; 27 continue; 28 } 29 if(j>n)break; 30 dp[i][j]=min(a[i]+dp[i+1][j],a[j]+dp[i][j-1]); 31 int temp=0; 32 for(int k=i+1;k<j;k++) 33 { 34 dp[i][j]=min(dp[i][j],dp[i][k-1]+a[k]+dp[k+1][j]); 35 } 36 dp[i][j]+=b[i-1]+b[j+1]; 37 } 38 } 39 cout<<"Case #"<<cas++<<": "; 40 cout<<dp[1][n]<<endl; 41 } 42 return 0; 43 }
H题
Happy Matt Friends
Time Limit: 6000/6000 MS (Java/Others) Memory Limit: 510000/510000 K (Java/Others)
Each of Matt’s friends has a magic number. In the game, Matt selects some (could be zero) of his friends. If the xor (exclusive-or) sum of the selected friends’magic numbers is no less than M , Matt wins.
Matt wants to know the number of ways to win.
For each test case, the first line contains two integers N, M (1 ≤ N ≤ 40, 0 ≤ M ≤ 10 6).
In the second line, there are N integers ki (0 ≤ k i ≤ 10 6), indicating the i-th friend’s magic number.

1 #include <iostream> 2 #include <cstring> 3 using namespace std; 4 int a[110]; 5 long long dp[2][(1<<20)+10]; 6 int main() 7 { 8 ios::sync_with_stdio(false); 9 int t; 10 cin>>t; 11 int cas=1; 12 while(t--) 13 { 14 int n,m; 15 cin>>n>>m; 16 memset(dp,0,sizeof(dp)); 17 for(int i=0;i<n;i++)cin>>a[i]; 18 cout<<"Case #"<<cas++<<": "; 19 dp[1][0]=1; 20 int k; 21 for(int i=0;i<n;i++) 22 { 23 for(int j=0;j<(1<<20);j++)dp[i&1][j]=dp[!(i&1)][j]; 24 for(int j=0;j<(1<<20);j++) 25 { 26 k=a[i]^j; 27 dp[i&1][k]+=dp[!(i&1)][j]; 28 } 29 } 30 long long ans=0; 31 for(int i=m;i<(1<<20);i++)ans+=dp[!(n&1)][i]; 32 cout<<ans<<endl; 33 } 34 return 0; 35 }
I题
Intersection
Time Limit: 4000/4000 MS (Java/Others) Memory Limit: 512000/512000 K (Java/Others)

A ring is a 2-D figure bounded by two circles sharing the common center. The radius for these circles are denoted by r and R (r < R). For more details, refer to the gray part in the illustration below.
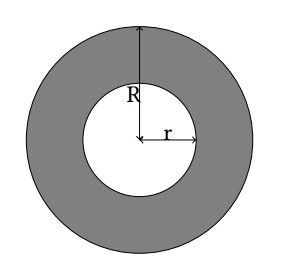
Matt just designed a new logo consisting of two rings with the same size in the 2-D plane. For his interests, Matt would like to know the area of the intersection of these two rings.
Each of the following two lines contains two integers x i, y i (0 ≤ x i, y i ≤ 20) indicating the coordinates of the center of each ring.

1 #include <iostream> 2 #include <cstring> 3 #include <iomanip> 4 #include <cmath> 5 #include <algorithm> 6 #include <cstdio> 7 using namespace std; 8 9 #define PI acos(-1.0) 10 double area(double x1,double y1,double r1,double x2,double y2,double r2) 11 { 12 double d=(x1-x2)*(x1-x2)+(y1-y2)*(y1-y2); 13 if(d>=(r1+r2)*(r1+r2))return 0; 14 if(d<=(r1-r2)*(r1-r2))return r1<r2 ? PI*r1*r1 : PI*r2*r2; 15 d=sqrt(d); 16 double a1=acos((r1*r1+d*d-r2*r2)/(2.0*r1*d)); 17 double a2=acos((r2*r2+d*d-r1*r1)/(2.0*r2*d)); 18 double s1=a1*r1*r1; 19 double s2=a2*r2*r2; 20 double t=(r1+r2+d)/2.0; 21 t=2.0*sqrt(t*(t-r1)*(t-r2)*(t-d)); 22 return s1+s2-t; 23 } 24 int main() 25 { 26 //ios::sync_with_stdio(false); 27 int t; 28 double r1,r2,x1,y1,x2,y2; 29 scanf("%d",&t); 30 int cas=1; 31 while(t--) 32 { 33 scanf("%lf%lf%lf%lf%lf%lf",&r1,&r2,&x1,&y1,&x2,&y2); 34 double ans=0; 35 ans-=area(x1,y1,r2,x2,y2,r1)*2; 36 ans+=area(x1,y1,r2,x2,y2,r2); 37 ans+=area(x1,y1,r1,x2,y2,r1); 38 printf("Case #%d: ",cas++); 39 printf("%.6lf\n",ans); 40 } 41 return 0; 42 }
K题
K.Bro Sorting
Time Limit: 2000/2000 MS (Java/Others) Memory Limit: 512000/512000 K (Java/Others)
Yesterday, K.Bro learnt an algorithm: Bubble sort. Bubble sort will compare each pair of adjacent items and swap them if they are in the wrong order. The process repeats until no swap is needed.
Today, K.Bro comes up with a new algorithm and names it K.Bro Sorting.
There are many rounds in K.Bro Sorting. For each round, K.Bro chooses a number, and keeps swapping it with its next number while the next number is less than it. For example, if the sequence is “1 4 3 2 5”, and K.Bro chooses “4”, he will get “1 3 2 4 5” after this round. K.Bro Sorting is similar to Bubble sort, but it’s a randomized algorithm because K.Bro will choose a random number at the beginning of each round. K.Bro wants to know that, for a given sequence, how many rounds are needed to sort this sequence in the best situation. In other words, you should answer the minimal number of rounds needed to sort the sequence into ascending order. To simplify the problem, K.Bro promises that the sequence is a permutation of 1, 2, . . . , N .
The second line contains N integers a i (1 ≤ a i ≤ N ), denoting the sequence K.Bro gives you.
The sum of N in all test cases would not exceed 3 × 10 6.
题意:求题目完成排序需要题目所述的最小的round次数
分析:每次把不符合排序的最大的数进行swap,那么,这个数在经过一个round之后,所有大于等于它的数一定是最终的排列。
由此,可以将问题转化为判断一个数的右边是否有必该数小的数,若有,则需要一次round。
对于此问题,只需要从右往左统计,并且不断更新最小值,若当前数为最小值,则将最小值更新为当前数,否则round+1

1 #include <iostream> 2 #include <cstdio> 3 using namespace std; 4 int a[1000010]; 5 int main() 6 { 7 ios::sync_with_stdio(false); 8 int n; 9 int t; 10 int cas=1; 11 scanf("%d",&t); 12 while(t--) 13 { 14 scanf("%d",&n); 15 int k,s=1,m=0; 16 int ans=0; 17 int minn=1e7; 18 for(int i=1;i<=n;i++) 19 { 20 scanf("%d",&a[i]); 21 } 22 for(int i=n;i>0;i--) 23 { 24 if(a[i]<minn)minn=a[i]; 25 else ans++; 26 } 27 printf("Case #%d: %d\n",cas++,ans); 28 29 } 30 return 0; 31 }
