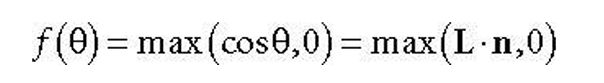Phong光照以及其他

    在说光照之前,有必要先弄清法线的变换,假设Mworld 将物体的定点一一变换到世界空间,如果我们对法线实施同样的变化,,以为能将法线变换到世界空间,但世界上变换之后的法线不再与表面垂直,就像下图:

    

    这意味着变换并不维持正交的性质,当然,不是所有的矩阵都会出现这种情况,只有当转换操作中包含非均匀缩放操作(XYZ各个方向缩放量不一样)时,这时候就不会再正交,这也意味着大部分的平移操作,旋转操作,均匀缩放操作或者上述组合都是能直接变换得,如何推导这个矩阵,方法有很多,(数学家们并未找出一个非常优雅的证明,我就从书上挪用下好了)

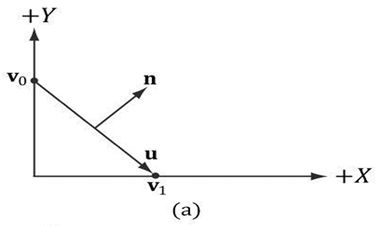
    显然,变换之前 : (V1 – V0)*n = 0;我们将其n转置,写成矩阵乘法((V1 – V0)* n^T = 0;),就是一个 1 * 2的矩阵 乘上一个 2*1的矩阵 ,为了简单起见,将V1 – V0 记做U,那么就是U* n^T = 0

    好了,开始推导,其实我们事先可以知道要求的目标矩阵是(Mworld )^{-1 T} 我们要找一个矩阵B 能使 (U* Mworld) * ( n * B) = 0,即维持正交特性,简单起见,将Mworld 记做A

    首先,由于要加入A的逆,我们便可以在原式里面插入 A^-1 _*A ,(注意,A总是可逆的) ,这样并不影响原式A^-1 _*A = I ,:即式子变成这样:u(AA^-1) n^T = 0

    注意,矩阵满足结合律,这样我们变可以将U与A结合尽量朝目标式子靠近 ,即: (uA)(A^-1 n^T) = 0

    由于我们还需要一次转置,于是我们对(A^-1 n^T) 实施两次转置,这样并不 改变结果,于是得到下式: (uA) ((A^-1 n^T)^T)^T = 0

    我们这下消去一些T,利用 (AB)^T = B^T A^T ，于是变成: (uA) (n(A^-1)^T)^T 注意这是个矩阵乘法,现在我们需要变换回来,又将其变回点积,即去掉最外面的那个T就行了:

        uA*n(A^-1)^T = 0

    结果已经出来了,即 B = (A^-1)^T 这是个证明而不是求导,希望读者注意到这一点,如何求导出来,读者自行研究吧

正题:光照

    现实中的光照何其炫丽,当然.这一切离不开物理学,首先进入Lamberat 余弦定理(定律?) 这是个很常见的现象,光照强度与法线和光照方向成的角度的余弦成正比,即:

        

    θ指的是L与N所成角度,L指光照方向,n是物体(表面)的法线方向,如果L,N都是标准化的那么 cosθ = L*n 很显然的,因为模长为1

    这个定理暂时放在这里,先简易介绍下Phong光照模型:

        事实上,光是非常复杂的,因为他具有波粒二向性,不考虑如此复杂的情况,也需要考虑对象表面处的入射辐射度已经抵达眼睛的出射辐射度,两者之间的关系可用BRDF描述,但是还是太复杂了(对于我来说).BRDF的简化版本并可通过Phong光照来模拟,实际上,实时光照效果伴随着GPU的发展已经逐渐脱离了Phong光照模型,尽管如此,从基础开始总是最好不过的了.

    Phong光照中,对象表面上一点的颜色由四项定义,即 漫反射(diffuse) ,镜面反射(specular),环境光(ambient)以及反射光.其中,漫反射和镜面反射来源于光源的光线,环境光用于模拟间接光照,发射光则是自发光对象了.接下来让我详细说之:

漫反射

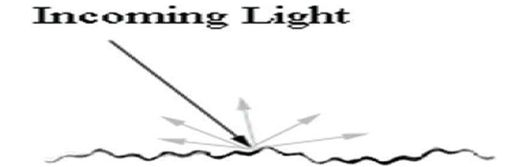
    考虑一个粗糙的表面,考虑最简单的光照情况,光照强度不随距离缩减,并到达一个表面时,沿着各个方向 均匀反射,由于反射光沿所有方向均匀反射,无论从那个方向观察,表面亮度均相同,使用时,无需考虑观测者的位置,至于Lamberat定理有关联(漫反射计算是视角独立的).一般的,将漫反射拆成两部分,一部分是光源的漫反射系数,一部分是材质的漫反射系数.将光照的记成Ld,材质的记为Md,那么反射光等于:

        C = Ld * Md * f(θ) = Ld * Md * max(L.n,0)

    各个方向均匀反射，所以不用考虑视点（相机）的位置

    环境光

    考虑到某些物体并没有处于光照的直接照射下，却某些部分会被照亮，因为其他物体对光的反射，想要模仿这类反射光，环境光是个不错的选择，由于光在场景中经多次反射并从各个方向抵达表明最终点，那么在各个方向上的以都是等强度的（这并不符合物理），这意味着，该光照与法线无关，也与视见方向无关，直接可以简单的写成 Sa * Ma

    镜面光

    前面已经说过粗糙平面，如果是光滑的如同镜子了，这个时候遵循反射定理，入射光和反射光与法线所成角度相等，但是值得注意的是，反射光不一定会朝着眼睛（相机）的方向，如下图

    

    这说明计算是视角依赖的，与角度的余弦成正比（反射方向与视角方向的夹角），为了更加健康的模拟此光照，当达到一定角度时，这种光照不贡献任何强度，有个近似的模拟强度的函数，函数如下

    （r*v） ^sh ，r为反射方向，v为眼睛和顶点所成的方向，sh表示对象表面的光滑程度，即模拟了达到一定角度时，强度贡献的衰弱，当然，只写成这样是有问题的，因为l，n的方向所成不一定是锐角，成〉=90度时是下面这种情况，还有就是r*v 小于0也是不正确的，所以，公式

    

    这是系数，然后再乘上Ss*Ms即得出了镜面反射

    至于发射光，可简单的定义为Me

我们已经简单的讲诉了光的几种成分，但没有区别光的不同类型，比如方向光，点关，聚光灯，下节再介绍了~