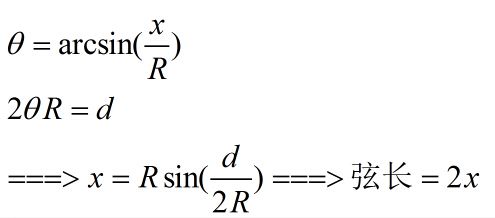#includeusingnamespacestd;intl,chance,rnd,win,lose,len2;chars[103],s2[106];voidguess(chara){intbad=1;for(inti=0;i
UVA 489 - Hangman Judge做题心得
Aleks_
ACM入门训练HangmanJudgeUVA489做题心得
HangmanJudgeIn``HangmanJudge,''youaretowriteaprogramthatjudgesaseriesofHangmangames.Foreachgame,theanswertothepuzzleisgivenaswellastheguesses.Rulesarethesameastheclassicgameofhangman,andaregivenasfoll
UVA 156 反片语
不想被人知道的黑暗面
UVA156反片语题目描述输入一些单词,找出所有满足如下条件的单词:该单词不能通过字母重排,得到输入文本中的另外一个单词。在判断是否满足条件时,字母不分大小写,但在输出时应保留输入中的大小写,按字典序进行排列(有大写字母在所有小写字母的前面)。样例输入laddercametapesoonleaderacmeRIDEloneDreispeatScAlEorbeyeRidesdealerNotEder
第十四节—GLSL语法
L_Ares
本文为L_Ares个人写作,如需转载请表明原文出处。GLSL语法和C语言的相似,但是GLSL中是没有指针的。另外,GLSL一般情况下都是没有语法提示的,所以最好不要写复杂的GLSL语言,除非你有业务需求,不然的话,很容易写错,而且找错也是很难的事情。一、变量和变量类型1.整型:int。代表至少包含16位的有符号的整数。可以是8进制,10进制,16进制。uint。无符号整型。例如:uintuValu
洛谷UVA题目Unknown Error
DBWG
洛谷OJ
UnexpectedResponseStatus:expectstatuscode:`301MovedPermanently`on`https://onlinejudge.org/index.php?option=com_comprofiler&task=login`,got:`200OK`如果你绑定了账号,去原站OnlineJudge-Home登录一下,好久没登陆,需要激活一下。我登录后再提交就
UVA11181条件概率 Probability|Given
DBWG
洛谷算法概率论
条件概率Probability|Given-洛谷|计算机科学教育新生态(luogu.com.cn)样例解释:需要学习条件概率和贝叶斯定理//12-0.1*0.2*(1-0.3)==0.014//1-30.1*0.8*0.3==0.024//-230.9*0.2*0.3==0.054//0.092//(0.014+0.024)/0.092==0.413043包含1的概率除以所有情况的概率之和就是1买
UVA11021 Tribles
DBWG
洛谷算法动态规划概率论期望DP
Tribles-洛谷|计算机科学教育新生态(luogu.com.cn)本题可以好好读读题,读输入那几个,我理解错题意还进行大量思考,可恶。。(我以为输入那几个是每种生物生或死的概率。非常低级的错误。)题意:开局给若干个生物,这个生物会在本回合发生以下行为后死掉:p0不生p1生1个p2生2个p3生3个...(这些概率p之和为1)样例解释:第一轮就得死光,0.33不生就死光了。解法——dp:我们设f[
Chapter 8 - 10. Congestion Management in TCP Storage Networks
mounter625
Linuxkerneltcp/ip网络网络协议linuxkernel
ComparisonwithLosslessNetworksAsChapter2explains,FibreChanneldefinesamaximumframesizeof2148bytes.UsersdonothavetochangetheMTUvalue,andhence,itisneveraconsideration.如第2章所述,光纤通道定义的最大帧大小为2148字节。用户无需更改MTU
亲子日记第十二篇
张正华_6a15
2018年8月11日昨天早上和付家欣一起刷牙的时候,她就问我,妈妈防晒是干什么用的?是防当太阳光的?我说不全是,最主要的是防太阳的紫外线的。妈妈,那什么是紫外线?上午没事的时候在店里查了一下,紫外线分为UVA(统称为短波,被大气层所吸收,对地球上的危害是最大的)UVB(统称为中波,会把皮肤晒伤,晒红,晒脱皮)UVA(统称为长波,会通过肌肤到达皮下组织,将皮肤晒黑,出现斑点).现在的孩子就是爱问问题
评价尤瓦尔·赫拉利
Jeep_9b89
尤瓦尔·赫拉利(YuvalNoahHarari),1976年生于以色列,牛津大学历史学博士,青年怪才、全球瞩目的新锐历史学家。现任耶路撒冷希伯来大学的历史系教授。它擅长世界历史和宏观历史进程研究,在学术领域和大众出版领域都有很大的兴趣。他的成就尤瓦尔·赫拉利的作品《人类简史》成为以色列超级畅销书,截至2016年,该书已授20多个国家版权,在历史学之外,人类学、生态学、基因学等领域的知识信手拈来,根
Guava Cache之开启统计信息收集
大风过岗
GauvaCache开启统计信息收集1.开启统计在创建Cache时,我们可以配置Cache让其开启统计信息收集,这样我们就可以对Cache的内存使用情况进行监控,并根据统计信息对cache进行调优,如果您的应用比较重视性能的话,可以开启这个特性。在创建Cache时,只需要调用recordStats()即可开启统计特性:开启统计2.开启一个后台线程完成统计信息的收集工作为了能够获取到缓存cache的
UVA11503 Virtual Friends 题解
见合8
题解c++算法
UVA11503VirtualFriends题解题目:原题面:题目描述PDF输入格式输出格式样例样例输入13FredBarneyBarneyBettyBettyWilma样例输出234翻译:有TTT组数据和nnn个关系,每个关系代表AAA和BBB是朋友关系(朋友的朋友也是朋友)。每次关系表时候,都要输出AAA和BBB所在朋友群中的人数。算法:并查集+哈希字符串怎么处理呢?可以用哈希来解决,用uno
DP UVALive 6506 Padovan Sequence
weixin_34347651
题目传送门/*题意:两行数字,相邻列一上一下,或者隔一列两行都可以,从左到右选择数字使和最大DP:状态转移方程:dp[i][j]=max(dp[i][j],dp[1-i][j-1]+a[i][j],dp[i/1-i][j-2]+a[i][j]);要从前面一个转态推过来啊,我比赛写反了,内功不够:(*/#include#include#include#include#include#include#
找规律 UVALive 6506 Padovan Sequence
weixin_33827965
题目传送门1/*2找规律:看看前10项就能看出规律,打个表就行了。被lld坑了一次:(3*/4#include5#include6#include7#include8#include9#include10#include11#include12#include13#include14#include15#include16usingnamespacestd;1718typedeflonglongl
数据挖掘(Data Mining, uva1591)
谭树杰的博客
成长日志数据挖掘uva
本题主要在于理解题意,Q数组可以不连续存储指的是只要公式能够满足即可,不一定有规律的存储。比如,先11个byte存储数据,1个byte空闲,再12个byte存储数据,1个byte空闲。简单计算可以得出K>=Sq*N为充要条件测试数据NortheasternEurope(NEERC)2003//uva1591.cpp#include#include#defineMAXN31intmain(){lon
uva508 莫尔斯电码(Morse Mismatches)
谭树杰的博客
成长日志uva
首先我理解错了题意,在这篇文章找到了UVa508MorseMismatches(莫尔斯电码)这题的意思是给定一些莫尔斯编码,给定一些已知字典,给定一些编码,求解这些编码的对应原文,如果可以精确匹配,则直接输出原单词,如果有多个可精确匹配的结果,则输出匹配结果里字典序最小的单词(紫书上说输出任意一个,这是错误的)并在末位加上“!”;如果无法精确匹配,则可以在编码的末尾增加或删除一些字符后匹配单词(增
青春的困境与代沟的消融
小板凳呀
青春的困境与代沟的消融中文名:野梨树外文名:Lepoiriersauvage/TheWildPearTree导演:努里·比格·锡兰编剧:阿克·阿克苏/埃布鲁·锡兰/努里·比格·锡兰主演:多古·德米尔科尔/穆拉特·塞米尔/本努伊·伊尔迪姆拉尔/哈扎尔·埃尔居奇卢/塞尔坎·克斯金/塔梅尔·莱文特/厄内尔·埃尔坎/里法特·桑贾尔/阿克·阿克苏/卡迪尔·瑟米克/欧扎·费什特类型:剧情国家:土耳其片长:18
312个免费高速HTTP代理IP(能隐藏自己真实IP地址)
yangshangchuan
高速免费superwordHTTP代理
124.88.67.20:843
190.36.223.93:8080
117.147.221.38:8123
122.228.92.103:3128
183.247.211.159:8123
124.88.67.35:81
112.18.51.167:8123
218.28.96.39:3128
49.94.160.198:3128
183.20
pull解析和json编码
百合不是茶
androidpull解析json
n.json文件:
[{name:java,lan:c++,age:17},{name:android,lan:java,age:8}]
pull.xml文件
<?xml version="1.0" encoding="utf-8"?>
<stu>
<name>java
[能源与矿产]石油与地球生态系统
comsci
能源
按照苏联的科学界的说法,石油并非是远古的生物残骸的演变产物,而是一种可以由某些特殊地质结构和物理条件生产出来的东西,也就是说,石油是可以自增长的....
那么我们做一个猜想: 石油好像是地球的体液,我们地球具有自动产生石油的某种机制,只要我们不过量开采石油,并保护好
类与对象浅谈
沐刃青蛟
java基础
类,字面理解,便是同一种事物的总称,比如人类,是对世界上所有人的一个总称。而对象,便是类的具体化,实例化,是一个具体事物,比如张飞这个人,就是人类的一个对象。但要注意的是:张飞这个人是对象,而不是张飞,张飞只是他这个人的名字,是他的属性而已。而一个类中包含了属性和方法这两兄弟,他们分别用来描述对象的行为和性质(感觉应该是
新站开始被收录后,我们应该做什么?
IT独行者
PHPseo
新站开始被收录后,我们应该做什么?
百度终于开始收录自己的网站了,作为站长,你是不是觉得那一刻很有成就感呢,同时,你是不是又很茫然,不知道下一步该做什么了?至少我当初就是这样,在这里和大家一份分享一下新站收录后,我们要做哪些工作。
至于如何让百度快速收录自己的网站,可以参考我之前的帖子《新站让百
oracle 连接碰到的问题
文强chu
oracle
Unable to find a java Virtual Machine--安装64位版Oracle11gR2后无法启动SQLDeveloper的解决方案
作者:草根IT网 来源:未知 人气:813标签:
导读:安装64位版Oracle11gR2后发现启动SQLDeveloper时弹出配置java.exe的路径,找到Oracle自带java.exe后产生的路径“C:\app\用户名\prod
Swing中按ctrl键同时移动鼠标拖动组件(类中多借口共享同一数据)
小桔子
java继承swing接口监听
都知道java中类只能单继承,但可以实现多个接口,但我发现实现多个接口之后,多个接口却不能共享同一个数据,应用开发中想实现:当用户按着ctrl键时,可以用鼠标点击拖动组件,比如说文本框。
编写一个监听实现KeyListener,NouseListener,MouseMotionListener三个接口,重写方法。定义一个全局变量boolea
linux常用的命令
aichenglong
linux常用命令
1 startx切换到图形化界面
2 man命令:查看帮助信息
man 需要查看的命令,man命令提供了大量的帮助信息,一般可以分成4个部分
name:对命令的简单说明
synopsis:命令的使用格式说明
description:命令的详细说明信息
options:命令的各项说明
3 date:显示时间
语法:date [OPTION]... [+FORMAT]
eclipse内存优化
AILIKES
javaeclipsejvmjdk
一 基本说明 在JVM中,总体上分2块内存区,默认空余堆内存小于 40%时,JVM就会增大堆直到-Xmx的最大限制;空余堆内存大于70%时,JVM会减少堆直到-Xms的最小限制。 1)堆内存(Heap memory):堆是运行时数据区域,所有类实例和数组的内存均从此处分配,是Java代码可及的内存,是留给开发人
关键字的使用探讨
百合不是茶
关键字
//关键字的使用探讨/*访问关键词private 只能在本类中访问public 只能在本工程中访问protected 只能在包中和子类中访问默认的 只能在包中访问*//*final 类 方法 变量 final 类 不能被继承 final 方法 不能被子类覆盖,但可以继承 final 变量 只能有一次赋值,赋值后不能改变 final 不能用来修饰构造方法*///this()
JS中定义对象的几种方式
bijian1013
js
1. 基于已有对象扩充其对象和方法(只适合于临时的生成一个对象):
<html>
<head>
<title>基于已有对象扩充其对象和方法(只适合于临时的生成一个对象)</title>
</head>
<script>
var obj = new Object();
表驱动法实例
bijian1013
java表驱动法TDD
获得月的天数是典型的直接访问驱动表方式的实例,下面我们来展示一下:
MonthDaysTest.java
package com.study.test;
import org.junit.Assert;
import org.junit.Test;
import com.study.MonthDays;
public class MonthDaysTest {
@T
LInux启停重启常用服务器的脚本
bit1129
linux
启动,停止和重启常用服务器的Bash脚本,对于每个服务器,需要根据实际的安装路径做相应的修改
#! /bin/bash
Servers=(Apache2, Nginx, Resin, Tomcat, Couchbase, SVN, ActiveMQ, Mongo);
Ops=(Start, Stop, Restart);
currentDir=$(pwd);
echo
【HBase六】REST操作HBase
bit1129
hbase
HBase提供了REST风格的服务方便查看HBase集群的信息,以及执行增删改查操作
1. 启动和停止HBase REST 服务 1.1 启动REST服务
前台启动(默认端口号8080)
[hadoop@hadoop bin]$ ./hbase rest start
后台启动
hbase-daemon.sh start rest
启动时指定
大话zabbix 3.0设计假设
ronin47
What’s new in Zabbix 2.0?
去年开始使用Zabbix的时候,是1.8.X的版本,今年Zabbix已经跨入了2.0的时代。看了2.0的release notes,和performance相关的有下面几个:
:: Performance improvements::Trigger related da
http错误码大全
byalias
http协议javaweb
响应码由三位十进制数字组成,它们出现在由HTTP服务器发送的响应的第一行。
响应码分五种类型,由它们的第一位数字表示:
1)1xx:信息,请求收到,继续处理
2)2xx:成功,行为被成功地接受、理解和采纳
3)3xx:重定向,为了完成请求,必须进一步执行的动作
4)4xx:客户端错误,请求包含语法错误或者请求无法实现
5)5xx:服务器错误,服务器不能实现一种明显无效的请求
J2EE设计模式-Intercepting Filter
bylijinnan
java设计模式数据结构
Intercepting Filter类似于职责链模式
有两种实现
其中一种是Filter之间没有联系,全部Filter都存放在FilterChain中,由FilterChain来有序或无序地把把所有Filter调用一遍。没有用到链表这种数据结构。示例如下:
package com.ljn.filter.custom;
import java.util.ArrayList;
修改jboss端口
chicony
jboss
修改jboss端口
%JBOSS_HOME%\server\{服务实例名}\conf\bindingservice.beans\META-INF\bindings-jboss-beans.xml
中找到
<!-- The ports-default bindings are obtained by taking the base bindin
c++ 用类模版实现数组类
CrazyMizzz
C++
最近c++学到数组类,写了代码将他实现,基本具有vector类的功能
#include<iostream>
#include<string>
#include<cassert>
using namespace std;
template<class T>
class Array
{
public:
//构造函数
hadoop dfs.datanode.du.reserved 预留空间配置方法
daizj
hadoop预留空间
对于datanode配置预留空间的方法 为:在hdfs-site.xml添加如下配置
<property>
<name>dfs.datanode.du.reserved</name>
<value>10737418240</value>
mysql远程访问的设置
dcj3sjt126com
mysql防火墙
第一步: 激活网络设置 你需要编辑mysql配置文件my.cnf. 通常状况,my.cnf放置于在以下目录: /etc/mysql/my.cnf (Debian linux) /etc/my.cnf (Red Hat Linux/Fedora Linux) /var/db/mysql/my.cnf (FreeBSD) 然后用vi编辑my.cnf,修改内容从以下行: [mysqld] 你所需要: 1
ios 使用特定的popToViewController返回到相应的Controller
dcj3sjt126com
controller
1、取navigationCtroller中的Controllers
NSArray * ctrlArray = self.navigationController.viewControllers;
2、取出后,执行,
[self.navigationController popToViewController:[ctrlArray objectAtIndex:0] animated:YES
Linux正则表达式和通配符的区别
eksliang
正则表达式通配符和正则表达式的区别通配符
转载请出自出处:http://eksliang.iteye.com/blog/1976579
首先得明白二者是截然不同的
通配符只能用在shell命令中,用来处理字符串的的匹配。
判断一个命令是否为bash shell(linux 默认的shell)的内置命令
type -t commad
返回结果含义
file 表示为外部命令
alias 表示该
Ubuntu Mysql Install and CONF
gengzg
Install
http://www.navicat.com.cn/download/navicat-for-mysql
Step1: 下载Navicat ,网址:http://www.navicat.com/en/download/download.html
Step2:进入下载目录,解压压缩包:tar -zxvf navicat11_mysql_en.tar.gz
批处理,删除文件bat
huqiji
windowsdos
@echo off
::演示:删除指定路径下指定天数之前(以文件名中包含的日期字符串为准)的文件。
::如果演示结果无误,把del前面的echo去掉,即可实现真正删除。
::本例假设文件名中包含的日期字符串(比如:bak-2009-12-25.log)
rem 指定待删除文件的存放路径
set SrcDir=C:/Test/BatHome
rem 指定天数
set DaysAgo=1
跨浏览器兼容的HTML5视频音频播放器
天梯梦
html5
HTML5的video和audio标签是用来在网页中加入视频和音频的标签,在支持html5的浏览器中不需要预先加载Adobe Flash浏览器插件就能轻松快速的播放视频和音频文件。而html5media.js可以在不支持html5的浏览器上使video和audio标签生效。 How to enable <video> and <audio> tags in
Bundle自定义数据传递
hm4123660
androidSerializable自定义数据传递BundleParcelable
我们都知道Bundle可能过put****()方法添加各种基本类型的数据,Intent也可以通过putExtras(Bundle)将数据添加进去,然后通过startActivity()跳到下一下Activity的时候就把数据也传到下一个Activity了。如传递一个字符串到下一个Activity
把数据放到Intent
C#:异步编程和线程的使用(.NET 4.5 )
powertoolsteam
.net线程C#异步编程
异步编程和线程处理是并发或并行编程非常重要的功能特征。为了实现异步编程,可使用线程也可以不用。将异步与线程同时讲,将有助于我们更好的理解它们的特征。
本文中涉及关键知识点
1. 异步编程
2. 线程的使用
3. 基于任务的异步模式
4. 并行编程
5. 总结
异步编程
什么是异步操作?异步操作是指某些操作能够独立运行,不依赖主流程或主其他处理流程。通常情况下,C#程序
spark 查看 job history 日志
Stark_Summer
日志sparkhistoryjob
SPARK_HOME/conf 下:
spark-defaults.conf 增加如下内容
spark.eventLog.enabled true spark.eventLog.dir hdfs://master:8020/var/log/spark spark.eventLog.compress true
spark-env.sh 增加如下内容
export SP
SSH框架搭建
wangxiukai2015eye
springHibernatestruts
MyEclipse搭建SSH框架 Struts Spring Hibernate
1、new一个web project。
2、右键项目,为项目添加Struts支持。
选择Struts2 Core Libraries -<MyEclipes-Library>
点击Finish。src目录下多了struts