POJ 2826 An Easy Problem?! --计算几何,叉积
题意: 在墙上钉两块木板,问能装多少水。即两条线段所夹的中间开口向上的面积(到短板的水平线截止)
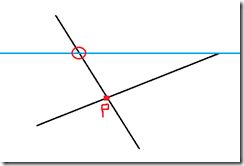
解法: 如图:
先看是否相交,不相交肯定不行,然后就要求出P与A,B / C,D中谁形成的向量是指向上方的。
然后求出y值比较小的,建一条水平线,求出与另一条的交点,然后求面积。
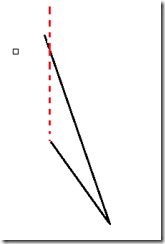
要注意的是:
这种情况是不能装水的,要判掉。
还有 交G++会WA, 交C++就可以了, 不知道是POJ的问题还是 G++/C++的问题。
代码:

#include <iostream> #include <cstdio> #include <cstring> #include <cstdlib> #include <cmath> #include <algorithm>
#define eps 1e-8
using namespace std; struct Point{ double x,y; Point(double x=0, double y=0):x(x),y(y) {} void input() { scanf("%lf%lf",&x,&y); } }; typedef Point Vector; int dcmp(double x) { if(x < -eps) return -1; if(x > eps) return 1; return 0; } template <class T> T sqr(T x) { return x * x;} Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); } Vector operator - (Vector A, Vector B) { return Vector(A.x - B.x, A.y - B.y); } Vector operator * (Vector A, double p) { return Vector(A.x*p, A.y*p); } Vector operator / (Vector A, double p) { return Vector(A.x/p, A.y/p); } bool operator < (const Point& a, const Point& b) { return a.x < b.x || (a.x == b.x && a.y < b.y); } bool operator >= (const Point& a, const Point& b) { return a.x >= b.x && a.y >= b.y; } bool operator <= (const Point& a, const Point& b) { return a.x <= b.x && a.y <= b.y; } bool operator == (const Point& a, const Point& b) { return dcmp(a.x-b.x) == 0 && dcmp(a.y-b.y) == 0; } double Dot(Vector A, Vector B) { return A.x*B.x + A.y*B.y; } double Length(Vector A) { return sqrt(Dot(A, A)); } double Angle(Vector A, Vector B) { return acos(Dot(A, B) / Length(A) / Length(B)); } double Cross(Vector A, Vector B) { return A.x*B.y - A.y*B.x; } bool SegmentIntersection(Point A,Point B,Point C,Point D) { return max(A.x,B.x) >= min(C.x,D.x) && max(C.x,D.x) >= min(A.x,B.x) && max(A.y,B.y) >= min(C.y,D.y) && max(C.y,D.y) >= min(A.y,B.y) && dcmp(Cross(C-A,B-A)*Cross(D-A,B-A)) <= 0 && dcmp(Cross(A-C,D-C)*Cross(B-C,D-C)) <= 0; } void SegIntersectionPoint(Point& P,Point a,Point b,Point c,Point d) //需保证ab,cd相交
{ P.x = (Cross(d-a,b-a)*c.x - Cross(c-a,b-a)*d.x)/(Cross(d-a,b-a)-Cross(c-a,b-a)); P.y = (Cross(d-a,b-a)*c.y - Cross(c-a,b-a)*d.y)/(Cross(d-a,b-a)-Cross(c-a,b-a)); } //Data Segment
Point A,B,C,D; //Data Ends
int main() { int t,i,j; scanf("%d",&t); while(t--) { A.input(), B.input(), C.input(), D.input(); if(!SegmentIntersection(A,B,C,D)) { puts("0.00"); continue; } Point P,Insec; SegIntersectionPoint(P,A,B,C,D); Vector PA = A-P, PB = B-P; Vector PC = C-P, PD = D-P; Point S1,S2,S3,S4,K1,K2; if(dcmp(PA.y) > 0) K1 = A; else if(dcmp(PB.y) > 0) K1 = B; else { puts("0.00"); continue; } if(dcmp(PC.y) > 0) K2 = C; else if(dcmp(PD.y) > 0) K2 = D; else { puts("0.00"); continue; } S3 = Point(K1.x,K1.y), S4 = Point(K1.x,10005); if(SegmentIntersection(S3,S4,P,K2)) { puts("0.00"); continue; } S3 = Point(K2.x,K2.y), S4 = Point(K2.x,10005); if(SegmentIntersection(S3,S4,P,K1)) { puts("0.00"); continue; } if(dcmp(K1.y-K2.y) < 0) { S1 = Point(-10005,K1.y), S2 = Point(10005,K1.y); SegIntersectionPoint(Insec,S1,S2,P,K2); printf("%.2f\n",fabs(Cross(K1-P,Insec-P)*0.5)); } else { S1 = Point(-10005,K2.y), S2 = Point(10005,K2.y); SegIntersectionPoint(Insec,S1,S2,P,K1); printf("%.2f\n",fabs(Cross(K2-P,Insec-P)*0.5)); } } return 0; }