POJ2942 Knights of the Round Table
| Time Limit: 7000MS | Memory Limit: 65536K | |
| Total Submissions: 4968 | Accepted: 1543 |
Description
Knights can easily get over-excited during discussions-especially after a couple of drinks. After some unfortunate accidents, King Arthur asked the famous wizard Merlin to make sure that in the future no fights break out between the knights. After studying the problem carefully, Merlin realized that the fights can only be prevented if the knights are seated according to the following two rules:
- The knights should be seated such that two knights who hate each other should not be neighbors at the table. (Merlin has a list that says who hates whom.) The knights are sitting around a roundtable, thus every knight has exactly two neighbors.
- An odd number of knights should sit around the table. This ensures that if the knights cannot agree on something, then they can settle the issue by voting. (If the number of knights is even, then itcan happen that ``yes" and ``no" have the same number of votes, and the argument goes on.)
Input
The input is terminated by a block with n = m = 0 .
Output
Sample Input
5 5 1 4 1 5 2 5 3 4 4 5 0 0
Sample Output
2
Hint
注明:转载出处:優YoU http://blog.csdn.net/lyy289065406/article/details/6756821
我觉得ta讲得不错,就是这样的,思维清晰,很好,不需要我多解释什么了。文字都转自ta那里,代码是我自己的,一A,忒爽。
大致题意:
亚瑟王要在圆桌上召开骑士会议,为了不引发骑士之间的冲突,并且能够让会议的议题有令人满意的结果,每次开会前都必须对出席会议的骑士有如下要求:
1、 相互憎恨的两个骑士不能坐在直接相邻的2个位置;
2、 出席会议的骑士数必须是奇数,这是为了让投票表决议题时都能有结果。
如果出现有某些骑士无法出席所有会议(例如这个骑士憎恨所有的其他骑士),则亚瑟王为了世界和平会强制把他剔除出骑士团。
现在给定准备去开会的骑士数n,再给出m对憎恨对(表示某2个骑士之间使互相憎恨的),问亚瑟王至少要剔除多少个骑士才能顺利召开会议?
注意:1、所给出的憎恨关系一定是双向的,不存在单向憎恨关系。
2、由于是圆桌会议,则每个出席的骑士身边必定刚好有2个骑士。即每个骑士的座位两边都必定各有一个骑士。
3、一个骑士无法开会,就是说至少有3个骑士才可能开会。
解题思路:
综合性非常强的图论题,在说解题报告之前,我建议大家先对以下内容有所认识,否则本题是很难做下去的:
1、补图 的定义
2、双连通分量 的定义
3、二分图 的定义
4、奇圈 的定义
5、判定一个图是否为二分图的方法:交叉染色法
6、Tarjan算法
上述知识点用于解决本题的重要性与其编号呈正相关。
最后要说一下的是,或者大家在看我这篇解题报告之前,已经看过其他解题报告,都不谋而合地给出了求割点的方法。
这里我声明一下:本题不需要求割点,我们仅仅是利用了Tarjan算法判定出现割点的过程以及条件而已,但我不建议用Tarjan算法去求无向图的割点,Tarjan算法只适用于求有向图的割点,直接套Tarjan模板用来求无向图割点会出错的。要求无向图的割点建议去看看刘汝佳的《算法艺术与信息学竞赛》,那里有详细方法。这些话与本题无关,我就不多说了。
==========================================================
为了方便大家做题,我这里大概第说一下上述的6个知识点,注意下述是我通俗的理解,不是标准定义:
1、 补图
图G的补图~G就是把图G原有的边全部删去,原本不存在的边全部连上。
2、双连通分量
简单来说,无向图G如果是双连通的,那么至少要删除图G的2个结点才能使得图G不连通。换而言之,就是图G任意2个结点之间都存在两条以上的路径连接(注意:路径不是指直接相连的边),那么双连通分量就是指无向图G的子图G’是双连通了。
3、二分图
二分图又叫二部图,这个百度百科有定义,了解一下二分图是什么样子的可以了,无需深入去了解。不懂得同学等到做二分图的题目时再认真学吧。
4、 奇圈
用一条线把奇数个点串连起来,所得到的闭合的圈就是奇圈了。其实奇圈就是有奇数个顶点的环。
5、交叉染色法判定二分图
初始化所有结点为无色(颜色0)状态,用DFS遍历一个图G的同时,顺便对结点染色(只染1、2色),注意遍历过的结点还可以再遍历重新上色。让遍历到某个时候在对结点t染色时,发现边s->t的另一个结点s已染色,且s的颜色与当前正在对t染的颜色相同,那么图G必定不是二分图。
这是因为想象一下二分图就像是河的两岸有两排结点,每染色一次则过河一次,那么相同颜色的结点必定在同一侧。一旦出现异侧有相同颜色的结点,就可以说明图G不是二分图了。
6、Tarjan算法
我希望大家主要去学习一下这个算法的基本原理,尤其是DFN数组和Low数组,还有什么是深搜树,什么是树枝边,什么是后向边。
学习一下Tarjan算法求割点的过程(注意我上文是建议大家不要用Tarjan算法去求解割点的题,但不是让大家不要看它求割点的过程),因为这个过程是求双连通分量的关键。
而如果想很好地了解Tarjan算法求割点的过程,还是建议先去看刘汝佳的《算法艺术与信息学竞赛》P285页,然后去做一下POJ1523(纯粹求割点的题)找点感觉。
只要弄懂了刘汝佳的方法,再看Tarjan算法就非常容易理解了。
给几个传送门:
有关图论的知识点的定义:http://www.byvoid.com/blog/biconnect/
我的POJ1523解题报告:http://blog.csdn.net/lyy289065406/article/details/6752662
Tarjan算法入门基础:
http://hi.baidu.com/lydrainbowcat/blog/item/42a6862489c98820c89559f3.html
Tarjan算法应用扩展:
http://hi.baidu.com/lydrainbowcat/blog/item/2194090a96bbed2db1351de8.html
===========================================================
有了上述知识支撑,可以开始解题了:
1、 利用m对憎恨对构造图G,则图G中有边相连的两个点表示这2个骑士互相憎恨。
2、 构造图G的补图~G,则图~G中有边相连的两个点表示这2个骑士可以坐在相邻位置。
3、 在图~G中,可能存在某些点的度数<=1,就是说这些骑士旁边最多只能坐另一个骑士,根据圆桌的座位要求每个骑士k的座位两边都必定各有一个骑士(k度数==2),那么我们认为这些度数<=1的点是孤立的或者是单连通的,也就是说他们不在圆桌的“环”内。
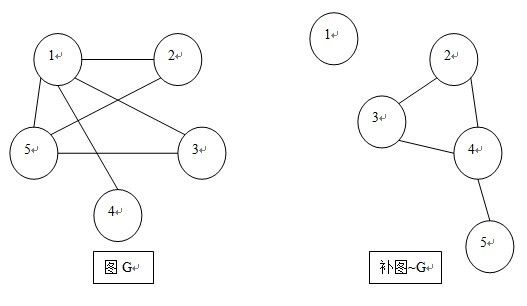
例如上图,我们利用图G构造补图~G后,显然骑士1的度=0,他是孤立的、不连通的;骑士5的度=1,他是单连通的;骑士{2,3,4}则构成一个双连通分量,他们正在圆桌“环”内开会。显然度数<=1的骑士1和骑士5都在环外,不满足出席会议的条件,亚瑟王为了维护世界和平自然会把这2人驱逐出骑士团。
4、 现在问题是,我们怎么才能知道哪些骑士在环外?
我们可以把问题转化为,我们怎么才能知道哪些骑士在环内?显然在环内的所有结点都是双连通的,我们可以通过Tarjan算法求双连通分量。注意,补图~G可能有几个双连通子图,即它可能有不止一组双连通分量,而Tarjan算法是一组一组双连通分量求出来的,因此每求出一组双连通分量我们就要马上处理一组。
下面都是针对某一组双连通分量的处理。
5、 骑士在双连通分量内(在环内),并不能就此就说明它可以出席会议了,因为假如这个骑士所在的双连通分量,不是一个奇数顶点的环(奇圈),而是一个偶数顶点的环,那么这个双连通分量内的全部骑士都要被亚瑟王开除。
6、 那么怎样判断一个双连通分量是奇圈呢?
首先我们要接受两条定理,想知道证明过程的可以上网找,这里不证明:
(1) 如果一个双连通分量内的某些顶点在一个奇圈中(即双连通分量含有奇圈),那么这个双连通分量的其他顶点也在某个奇圈中;
(2) 如果一个双连通分量含有奇圈,则他必定不是一个二分图。反过来也成立,这是一个充要条件。
由于双连通分量也是一个图,那么要判断双连通分量是否为奇圈,只需判断这个双连通分量是否为一个二分图,而要判断一个图是否为二分图,就用交叉染色法!
7、 显然所有在奇圈中的骑士,都是允许出席会议的,而由于可能有部分骑士允许出席一个以上的会议(即他们是2个以上的奇圈的公共点),那么为了避免重复统计人数,当我们判断出哪些骑士允许出席会议时,就把他们做一个标记(相同的骑士只做一个标记)。最后当Tarjan算法结束后,我们统计一下被标记的人数有多少,再用总人数减去这部分人,剩下的就是被亚瑟王剔除的人数了。
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <stack>
#include <vector>
#define MIN(a,b) ((a)<(b)?(a):(b))
#define N 1005
using namespace std;
vector<int>gra[N],ans;
int G[N][N];
int dfn[N],low[N],vis[N],now,id,flag[N],col[N];
int n,m;
stack<int>sta;
void ini(void)//初始化
{
memset(G,0,sizeof(G));
memset(dfn,0,sizeof(dfn));
memset(low,0,sizeof(low));
memset(flag,0,sizeof(flag));
now=id=0;
while(sta.empty()==0)sta.pop();
for(int i=1;i<=n;i++)
gra[i].clear();
}
int dfs(int s,int c)//交叉染色法判断这个爽连通分量是否含有奇圈,s为点,c为具体的颜色,1或0
{
vis[s]=0;//为了编程方便,改了一下,vis为1时表示这个点未访问,vis为0是表示这个点已经访问
col[s]=c;
c=1-c;//改变颜色
for(int i=0;i<gra[s].size();i++)
{
int t=gra[s][i];
if(col[t]!=-1&&col[t]!=c)return 1;
if(vis[t]==1&&dfs(t,c))return 1;
}
return 0;
}
void tarjan(int s,int p)
{
dfn[s]=low[s]=++now;
sta.push(s);
for(int i=0;i<gra[s].size();i++)
{
int t=gra[s][i];
if(!dfn[t])
{
tarjan(t,s);
low[s]=MIN(low[s],low[t]);
if(low[t]>=dfn[s])//当该点为割点的时候
{
memset(vis,0,sizeof(vis));//vis为0表示已经访问,为1表示这些点等待访问
memset(col,-1,sizeof(col));//col=-1表示无颜色
ans.clear();//记录这时候的连通分量里面的点
while(sta.empty()==0)
{
int k=sta.top();
sta.pop();
ans.push_back(k);
vis[k]=1;
if(k==t)break;
}
vis[s]=1;
ans.push_back(s);
if(dfs(s,1))
for(int j=0;j<ans.size();j++)
flag[ans[j]]=1;//flag记录这个点是否可以参加会议
}
}
else
if(t!=p)
low[s]=MIN(low[s],dfn[t]);
}
}
int main()
{
while(scanf("%d%d",&n,&m),n+m)
{
ini();
for(int i=1;i<=m;i++)
{
int a,b;
scanf("%d%d",&a,&b);
G[a][b]=G[b][a]=1;//G为原来的图
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(G[i][j]==0&&i!=j)
gra[i].push_back(j);//gra为G的补图
for(int i=1;i<=n;i++)
if(!dfn[i])
{
while(!sta.empty())sta.pop();
tarjan(i,0);
}
int sum=n;
for(int i=1;i<=n;i++)
if(flag[i])sum--;
printf("%d\n",sum);
}
}