Pick-up sticks(判断两条线段是否相交)
| Time Limit: 3000MS | Memory Limit: 65536K | |
| Total Submissions: 8351 | Accepted: 3068 |
Description
Stan has n sticks of various length. He throws them one at a time on the floor in a random way. After finishing throwing, Stan tries to find the top sticks, that is these sticks such that there is no stick on top of them. Stan has noticed that the last thrown stick is always on top but he wants to know all the sticks that are on top. Stan sticks are very, very thin such that their thickness can be neglected.
Input
Input consists of a number of cases. The data for each case start with 1 <= n <= 100000, the number of sticks for this case. The following n lines contain four numbers each, these numbers are the planar coordinates of the endpoints of one stick. The sticks are listed in the order in which Stan has thrown them. You may assume that there are no more than 1000 top sticks. The input is ended by the case with n=0. This case should not be processed.
Output
For each input case, print one line of output listing the top sticks in the format given in the sample. The top sticks should be listed in order in which they were thrown.
The picture to the right below illustrates the first case from input.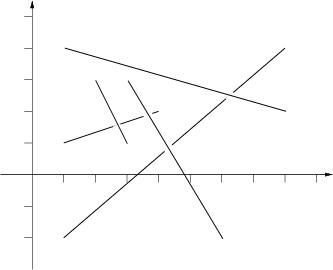
The picture to the right below illustrates the first case from input.

Sample Input
5 1 1 4 2 2 3 3 1 1 -2.0 8 4 1 4 8 2 3 3 6 -2.0 3 0 0 1 1 1 0 2 1 2 0 3 1 0
Sample Output
Top sticks: 2, 4, 5. Top sticks: 1, 2, 3.
题意:给n个木条,每条线段元素包含四个数,分别是其端点的横纵坐标,n个木条依次按先后顺序扔出,问放在最上面的木条的序号;
思路:判断两条线段相交问题,判断每个木条与它后面的木条是否相交,若相交,则当前木条肯定不是最上面的,用标记数组进行标记,最后遍历一遍输出序号就可以了;

1 #include<stdio.h> 2 #include<algorithm> 3 #include<math.h> 4 using namespace std; 5 const int maxn = 100010; 6 7 struct point 8 { 9 double x,y; 10 point(){} 11 point(double a,double b):x(a),y(b) {} 12 friend point operator - (const point &a,const point &b) 13 { 14 return point(a.x-b.x,a.y-b.y); 15 } 16 friend double operator ^(const point &a,const point &b) 17 { 18 return a.x*b.y-a.y*b.x; 19 } 20 friend double operator *(const point &a, const point &b) 21 { 22 return a.x*b.x + a.y*b.y; 23 } 24 }; 25 26 struct line 27 { 28 point a; 29 point b; 30 int flag; 31 line (){} 32 line (point x, point y):a(x),b(y) {} 33 }L[maxn]; 34 35 const double eps = 1e-8; 36 int cmp(double x) 37 { 38 if(fabs(x) < eps) 39 return 0; 40 if(x > 0) 41 return 1; 42 return -1; 43 } 44 45 bool inter(line L1, line L2)//判断两条线段是否相交 46 { 47 return 48 //快速排斥实验 49 max(L1.a.x,L1.b.x) >= min(L2.a.x,L2.b.x) && 50 max(L2.a.x,L2.b.x) >= min(L1.a.x,L1.b.x) && 51 max(L1.a.y,L1.b.y) >= min(L2.a.y,L2.b.y) && 52 max(L2.a.y,L2.b.y) >= min(L1.a.y,L1.b.y) && 53 //跨立实验 54 cmp((L2.a-L1.a)^(L1.b-L1.a))*cmp((L2.b-L1.a)^(L1.b-L1.a)) <= 0 && 55 cmp((L1.a-L2.a)^(L2.b-L2.a))*cmp((L1.b-L2.a)^(L2.b-L2.a)) <= 0; 56 } 57 58 int main() 59 { 60 int n; 61 while(~scanf("%d",&n) && n) 62 { 63 double x1,y1,x2,y2; 64 struct point p1,p2; 65 for(int i = 0; i < n; i++) 66 { 67 scanf("%lf %lf %lf %lf",&x1,&y1,&x2,&y2); 68 p1.x = x1; 69 p1.y = y1; 70 p2.x = x2; 71 p2.y = y2; 72 L[i].a = p1; 73 L[i].b = p2; 74 L[i].flag = 1; 75 } 76 77 for(int i = 0; i < n-1; i++) 78 { 79 for(int j = i+1; j < n; j++) 80 { 81 if(inter(L[i],L[j]))//如果第i条线段与第j条线段(i<j)相交,第i条线段显然不可能是最上边的; 82 { 83 L[i].flag = 0; 84 break; 85 } 86 } 87 } 88 89 printf("Top sticks:"); 90 int ok = 0; 91 for(int i = 0; i < n; i++) 92 { 93 if(L[i].flag == 1) 94 { 95 if(ok == 0) 96 { 97 printf(" %d",i+1); 98 ok = 1; 99 } 100 else printf(", %d",i+1); 101 } 102 } 103 printf(".\n"); 104 105 } 106 return 0; 107 }
判断两条线段是否相交问题:
(1) 快速排斥试验
设以线段 P1P2 为对角线的矩形为 R , 设以线段 Q1Q2 为对角线的矩形为 T ,如果 R 和 T
不相交,显然两线段不会相交。
(2) 跨立试验
如果两线段相交,则两线段必然相互跨立对方。若 P1P2 跨立 Q1Q2 ,则矢量 ( P1 - Q1 ) 和
( P2 - Q1 ) 位于矢量 ( Q2 - Q1 ) 的两侧,
即 ( P1 - Q1 ) × ( Q2 - Q1 ) * ( P2 - Q1 ) × ( Q2 - Q1 ) < 0 。
上式可改写成 ( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) > 0 。
当 ( P1 - Q1 ) × ( Q2 - Q1 ) = 0 时,说明 ( P1 - Q1 ) 和 ( Q2 - Q1 ) 共线,
但是因为已经通过快速排斥试验,所以 P1 一定在线段 Q1Q2 上;
同理, ( Q2 - Q1 ) ×(P2 - Q1 ) = 0 说明 P2 一定在线段 Q1Q2 上。
所以判断 P1P2 跨立 Q1Q2 的依据是:
( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) >= 0 。
同理判断 Q1Q2 跨立 P1P2 的依据是:
( Q1 - P1 ) × ( P2 - P1 ) * ( P2 - P1 ) × ( Q2 - P1 ) >= 0 。
当快速排斥实验和跨立实验都满足时,才说明两天线段相交;
