Silverlight.XNA(C#)跨平台3D游戏研发手记：(二)四叉树遍历与人工智能A*算法在SLG移动路径范围测算中的应用

    除战斗范围设定外，说到SLG中最有趣而经典的算法莫过于角色可移动范围的测算与寻路。当前成熟的SLG商业游戏中，以《火焰纹章》、《高级大战争》等系列新作为代表，它们在传统的基础上将可移动范围进行了拓展，组合上攻击范围并配合移动指向路径箭头，使得整场战局每个“棋子”的操控感受和趣味性都无与伦比。

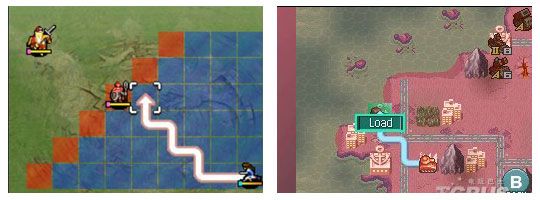
SLG角色移动从程序设计的角度可大致分为3个步骤：

1）呈现可移动路径范围

2）确定移动目的地单元格

3）沿着路径移动到目的地

以四向为基础的Silverlight 2D SLG游戏，我们首先想到的当然是采用四叉树遍历算法来实现其中的角色可移动路径范围测算。

不要被它的行头所吓到，其实它只是一种很简单的四向延展循环遍历，我们不妨先来看下图：

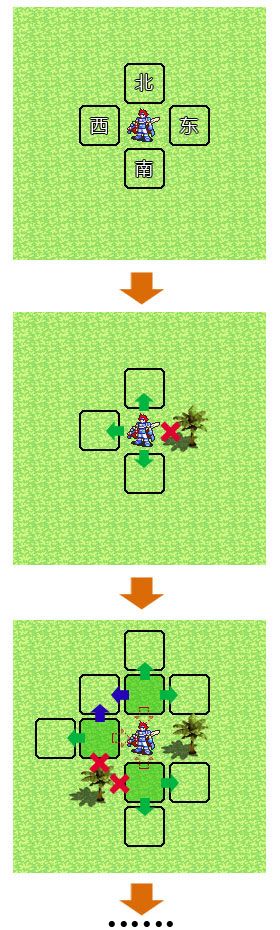
每个角色以其所处的格子(坐标)为中心，第一步可移动的格子只有：北、东、南、西；那么要测算其可移动范围，首先得分析周围这4个格子角色是否可以移动到，其中判断的依据有地形矩阵边界、机动力极限（或四叉树深度）以及地形机动力消耗等元素；如果判断为可行，则将此格子进行标记(存储进可移动范围List<Point>表中)；接下来再以同样的步骤，分别以这些被标记过的格子为中心，继续四向延伸遍历 (以减去当前单元格机动力消耗为基础)；额外的，此时除了判断是否可以移动外，还需判断子节点是否有效(List中是否存在重复，如果重复哪一个Path的机动力消耗最小则替换掉，Path是否回头等逻辑)。于是，最终我们可以得出类似如下算法：

         ///   <summary>
         ///  显示可移动范围路径
         ///   </summary>
         public  void ShowPathRange(Sprite sprite) {
            sprite.PathRange.Clear();
            ClearAllRange();
            Dictionary<Point2D,  int> rangeList =  new Dictionary<Point2D,  int>();
            Dictionary<Point2D,  int> tempList =  new Dictionary<Point2D,  int>();
            Point2D center =  new Point2D(( int)sprite.Coordinate.X, ( int)sprite.Coordinate.Y);
            rangeList.Add(center,  0);
            tempList.Add(center,  0);
             int countPoint =  0;
             while (countPoint < sprite.Mov) {
                tempList = RangeScan(tempList, rangeList, sprite.Mov);
                countPoint++;
            }
             // 绘制所有格子
             for ( int i =  0; i < rangeList.Count; i++) {
                Point p = rangeList.ElementAt(i).Key.ToPoint();
                sprite.PathRange.Add(p);
                EntityObject box =  new EntityObject() {
                    Source = GetImage( " MoveBox.png "),
                    Position = GetPositionFromCoordinate(p),
                };
                pathRangeSystem.Children.Add(box);
                MouseButtonEventHandler handler= null;
                box.MouseLeftButtonDown += handler =  delegate {
                    box.MouseLeftButtonDown -= handler;
                    sprite.MoveTo(p, Matrix);
                };
            }
        }

         ///   <summary>
         ///  四叉树遍历扫描
         ///   </summary>
        Dictionary<Point2D,  int> RangeScan(Dictionary<Point2D,  int> tempList, Dictionary<Point2D,  int> rangeList,  int moveLimit) {
            Dictionary<Point2D,  int> result =  new Dictionary<Point2D,  int>();
             for ( int i =  0; i < tempList.Count; i++) {
                KeyValuePair<Point2D,  int> kvp = tempList.ElementAt(i);
                DirectionScan( new Point2D(kvp.Key.X, kvp.Key.Y -  1), kvp.Value, result, rangeList, moveLimit);  // 北
                DirectionScan( new Point2D(kvp.Key.X +  1, kvp.Key.Y), kvp.Value, result, rangeList, moveLimit);  // 东
                DirectionScan( new Point2D(kvp.Key.X, kvp.Key.Y +  1), kvp.Value, result, rangeList, moveLimit);  // 南
                DirectionScan( new Point2D(kvp.Key.X -  1, kvp.Key.Y), kvp.Value, result, rangeList, moveLimit);  // 西
            }
             return result;
        }

         ///   <summary>
         ///  基于方向的扫描
         ///   </summary>
         void DirectionScan(Point2D direction,  int matrix, Dictionary<Point2D,  int> tempList, Dictionary<Point2D,  int> range,  int moveLimit) {
             if (!range.ContainsKey(direction) && IsEffectivelyCoordinate(direction) && Matrix[direction.X, direction.Y] !=  0) {
                 int value = matrix + Matrix[direction.X, direction.Y];
                 if (value <= moveLimit) {
                    if (!tempList.ContainsKey(direction)) {
                        tempList.Add(direction, value);
                    } else if (value < tempList[direction]) { //各方向到达同一地点，只取最小机动力消耗
                        tempList[direction] = value;
                    }
                    if (!range.ContainsKey(direction)) {
                        range.Add(direction, value);
                    }                

                }
            }
        }

         ///   <summary>
         ///  坐标是否有效
         ///   </summary>
         bool IsEffectivelyCoordinate(Point2D p) {
             return p.X >=  0 && p.Y >=  0 && p.X < dimension && p.Y < dimension ?  true :  false;
        }

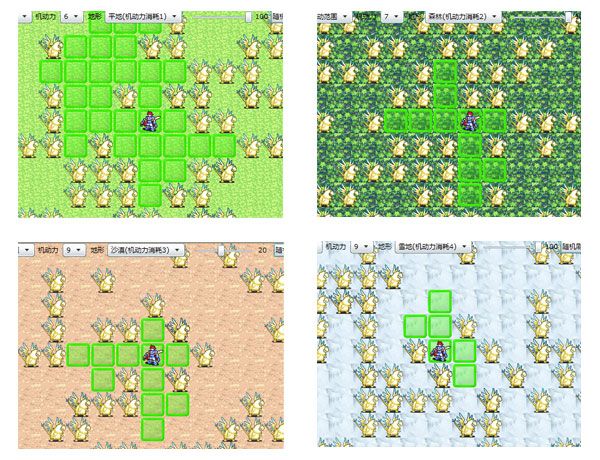
顺便说明一下，SLG地形设计千变万化，本节中我仅仅设置了5种地形：障碍(无法通行)、平原/草地(机动力消耗1)、森林/丘陵 (机动力消耗2)、沙漠/沼泽(机动力消耗3)、山地(机动力消耗4)、河流(机动力消耗5)等，其枚举如下（对应的枚举值也是该地形的机动力消耗，当然实际情况要比这复杂，比如不同地形相同机动力消耗等）：

     ///   <summary>
     ///  地形类型
     ///   </summary>
     public  enum TerrainTypes {
         ///   <summary>
         ///  障碍
         ///   </summary>
        Obstacle =  0,
         ///   <summary>
         ///  平地
         ///   </summary>
        Ground =  1,
         ///   <summary>
         ///  森林
         ///   </summary>
        Forest =  2,
         ///   <summary>
         ///  沙漠
         ///   </summary>
        Desert =  3,
         ///   <summary>
         ///  雪地
         ///   </summary>
        Snow =  4,
    }

当我们计算并呈现完角色可移动范围后，接下来玩家便需要指挥角色向目标位置移动，人工智能A*算法又一次的派上了用场；Silverlight中我们可以通过创建Storyboard关键帧动画的简单形式配合上A*算法得到的Path路径点轻松实现非对角线式的角色寻路移动（其中的A*代码为国外高人编写，可参考我曾写过的一篇文章，本文就不再班门弄斧了）。：

关键帧动画A*寻路移动

         ///   <summary>
         ///  A*寻路向目的地移动
         ///   </summary>
         public  void MoveTo(Point destination,  byte[,] matrix) {
            PathFinderFast pathFinderFast =  new PathFinderFast(matrix) {
                Diagonals =  false,
                HeuristicEstimate =  2,
                SearchLimit =  1000,
            };
            List<PathFinderNode> path = pathFinderFast.FindPath( new Point2D() {
                X = ( int)Coordinate.X,
                Y = ( int)Coordinate.Y
            },  new Point2D() {
                X = ( int)destination.X,
                Y = ( int)destination.Y
            });
             if (path ==  null || path.Count <  1) {
                 // 路径不存在
                 return;
            }  else {
                PointAnimationUsingKeyFrames pointAnimationUsingKeyFrames =  new PointAnimationUsingKeyFrames() {
                    Duration =  new Duration(TimeSpan.FromMilliseconds((path.Count -  1) * speed))
                };
                Storyboard.SetTarget(pointAnimationUsingKeyFrames,  this);
                Storyboard.SetTargetProperty(pointAnimationUsingKeyFrames,  new PropertyPath( " Coordinate "));
                 // 匀速关键帧
                 for ( int i = path.Count -  1; i >=  0; i--) {
                    pointAnimationUsingKeyFrames.KeyFrames.Add(
                         new LinearPointKeyFrame() {
                            KeyTime = KeyTime.FromTimeSpan(TimeSpan.FromMilliseconds((path.Count -  1 - i) * speed)),
                            Value =  new Point(path[i].X, path[i].Y)
                        }
                    );
                }
                storyboard.Pause();
                storyboard.Completed -= storyboard_Completed;
                storyboard =  new Storyboard();
                storyboard.Children.Add(pointAnimationUsingKeyFrames);
                storyboard.Completed +=  new EventHandler(storyboard_Completed);
                storyboard.Begin();
            }
        }

这是一款基于Silverlight的SLG游戏引擎的一部分，在线演示Demo 如下(点击下载该Demo源码)，大家不妨刷刷怪和地形，然后移动角色试试，非常有趣：

手记感悟：回想之前曾写过的一个三国策的SLG Demo，为了省事，当时写的移动范围算法其实是错误的；大量测试证明，SLG中的移动范围不能使用A*寻路算法替代，虽然看上去似乎减少了工作量，但实际操作过程中你会发现对可及范围所有格子都使用一次A*算法极其消耗性能；另外，就目前我所用到的A*算法来说，根本就无法正确显示角色的可移动范围(由于A*算法原理所致)，要么漏掉几格，要么多出几格，越是复杂且障碍物无规律的地形表现越突出。

手记小结：通过四叉树遍历算法可以很有趣的将SLG游戏角色可移动范围形象化、直观化，此算法的实现和优化无止尽，仁者见仁智者见智，期待您更优秀的实现，让思维的创新来得更猛烈些吧！