zoj 1986 Bridging Signals

ZOJ Problem Set - 1986

Bridging Signals

---

Time Limit: 1 Second      Memory Limit: 32768 KB

---

'Oh no, they've done it again', cries the chief designer at the Waferland chip factory. Once more the routing designers have screwed up completely, making the signals on the chip connecting the ports of two functional blocks cross each other all over the place. At this late stage of the process, it is too expensive to redo the routing. Instead, the engineers have to bridge the signals, using the third dimension, so that no two signals cross. However, bridging is a complicated operation, and thus it is desirable to bridge as few signals as possible. The call for a computer program that finds the maximum number of signals which may be connected on the silicon surface without crossing each other, is imminent. Bearing in mind that there may be thousands of signal ports at the boundary of a functional block, the problem asks quite a lot of the programmer. Are you up to the task?

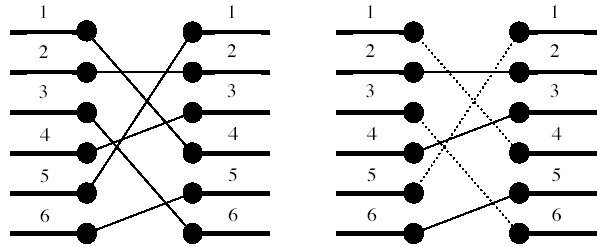
Figure 1. To the left: The two blocks' ports and their signal mapping (4, 2, 6, 3, 1, 5). To the right: At most three signals may be routed on the silicon surface without crossing each other. The dashed signals must be bridged.

A typical situation is schematically depicted in figure 1. The ports of the two functional blocks are numbered from 1 to p, from top to bottom. The signal mapping is described by a permutation of the numbers 1 to p in the form of a list of p unique numbers in the range 1 to p, in which the ith number specifies which port on the right side should be connected to the ith port on the left side. Two signals cross if and only if the straight lines connecting the two ports of each pair do.

Input

On the first line of the input, there is a single positive integer n, telling the number of test scenarios to follow. Each test scenario begins with a line containing a single positive integer p < 40000, the number of ports on the two functional blocks. Then follow p lines, describing the signal mapping:

On the ith line is the port number of the block on the right side which should be connected to the ith port of the block on the left side.

Output

For each test scenario, output one line containing the maximum number of signals which may be routed on the silicon surface without crossing each other.

Sample Input

4
6
4
2
6
3
1
5
10
2
3
4
5
6
7
8
9
10
1
8
8
7
6
5
4
3
2
1
9
5
8
9
2
3
1
7
4
6

Sample Output

3
9
1
4

---

Source: Northwestern Europe 2003
Submit    Status

---

// 1853603 2009-05-04 15:42:41 Accepted  1986 C++ 80 652 Wpl 
#include  < iostream >
#define  MAX 40005   // 10 
using   namespace  std;
int  n,data[MAX],M,t;
int  dp[MAX],c[MAX];  // c数组的含义是c[dp[k]]=data[k];即当递增子序列的长度为dp[k]时子序列的末尾元素是data[k]
void  Init()
{
  int  i;
 scanf( " %d " , & n);
  for (i = 1 ;i <= n;i ++ )
 {
  scanf( " %d " , & data[i]);
  c[i] = MAX;      // 这里实际上是初始化为最大的序列长度
 }
}
int  Find( int   * a, int  len, int  n)
{
  int  left,right,mid;
 left = 1 ;
 right = n;
 mid = (left + right) / 2 ;
  while (left <= right)
 {
   if (n > a[mid])
   left = mid + 1 ;
   else   if (n < a[mid])
   right = mid - 1 ;
   else
    return  mid;
  mid = (left + right) / 2 ;
 }
  return  left;
}
int  LongLcs()
{
  int  i,mmax,j,k;
 M = 1 ;
 c[ 1 ] = data[ 1 ];
 dp[ 1 ] = 1 ;
  for (i = 2 ;i <= n;i ++ )
 {
  j = Find(c,n + 1 ,data[i]);
  c[j] = data[i];
  dp[i] = j;
   if (j > M)
   M = j;
 }
  return  M;
}
int  main()
{
 scanf( " %d " , & t);
  while (t -- )
 {
  Init();
   int  len = LongLcs();
  printf( " %d\n " ,len);
 }
  return   0 ;
}