音频处理3_时域频域

本节主要讲音频的时域到频域的变换和理解

我们以两个正弦波的组合信号为例，生成代码如下：

# 生成信号
t = np.linspace(0, 1, 1000, endpoint=False) # 时间轴 
freq1 = 5 # 5 Hz
freq2 = 20 # 20 Hz 
signal = np.sin(2 * np.pi * freq1 * t) + 0.5 * np.sin(2 * np.pi * freq2 * t) 
# 合成信号

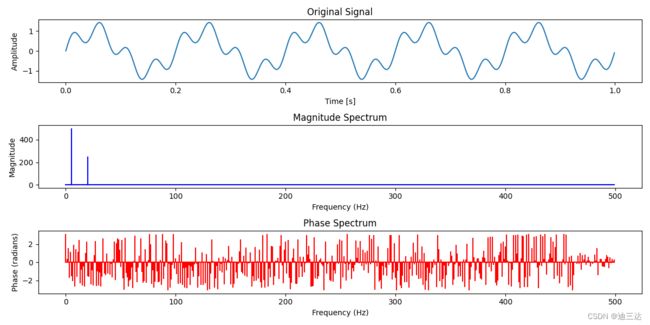
第1幅图是时域图，第2-3幅图是频率图，分别记录不同频率波的幅度值和起始点(相位角)：

1. 时域

x是时间，y是音波在特定时间点的气压偏移量，如音压值、电压信号的电压值,
也可以理解为声波的幅值。

绘制时域图：

# 绘制原始信号
plt.figure(figsize=(12, 6))
plt.subplot(3, 1, 1)
plt.plot(t, signal)
plt.title('Original Signal')
plt.xlabel('Time [s]')
plt.ylabel('Amplitude')

2.频域

把时域信息转换为频域，需要把时间信息去掉，频域只有t=0时刻的信息：

• x坐标轴：由时间变为频率，即x轴代表不同波的频率

• y坐标轴：由气压值转换为波的振幅大小(幅度谱) 和 波的起始相位角(相位谱)

换个角度理解，频域是把音频拆解为不同频率的正弦波（有周期性规律），并记录每个波的“幅度值”和“0时刻各个波的“起始位置”。

2.1 傅立叶变换

傅里叶变换的结果是一个复数序列$X(f)$.

f为频率值(x坐标)，虚数单位为j，变换公式如下：$X(f)=A(f)\cdot e^{j\varphi (f)}$

幅度谱（Magnitude Spectrum）：A(f) 表示频率f处的幅度，是一个正值。

相位谱（Phase Spectrum）：ϕ(f) 是频率f 处的相位角, 时间t=0。

傅里叶变换：信号表示为复数, 欧拉公式有: $e^{j\varphi }=cos(\varphi )+jsin(\varphi )$

幅度为0的数，相位角可以为任意值
(零复数在复平面上没有明确的方向，因此相位未定义或多值)。

# 计算傅里叶变换
fft_result = np.fft.fft(signal)

# 计算频率轴
freqs = np.fft.fftfreq(len(signal), d=t[1] - t[0])

2.2 幅度谱

幅度谱也叫频谱图，因为该信号只有两个正选波，因此幅度谱上只会有这两个频率波的幅值。

代码如下：

magnitude = np.abs(fft_result) # 提取幅度信息

# 绘制幅度谱
plt.subplot(3, 1, 2)
plt.stem(freqs[:len(freqs)//2], magnitude[:len(freqs)//2], 'b', markerfmt=" ", basefmt="-b")
plt.title('Magnitude Spectrum')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')

通过对幅度取log提升人类对幅度的感知

2.3 相位谱

相位: 音频信号的每个频率成分在0时刻的相位角(theta).

也可以理解为音频的起点时刻，各频率波的起始角(theta).

• theta=0度，t=0时刻该频率波f周期性地从0开始上升

• theta=90度，t=0时刻该频率波f周期性地从最大值开始下降

代码如下：

phase = np.angle(fft_result)  # # 提取相位信息

# 绘制相位谱
plt.subplot(3, 1, 3)
plt.stem(freqs[:len(freqs)//2], phase[:len(phase)//2], 'r', markerfmt=" ", basefmt="-r")
plt.title('Phase Spectrum')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Phase (radians)')
plt.tight_layout()
plt.show()

3. 逆变换：波谱转音频

3.1 时域转音频

将时域信号转换为音频时，音质可能会因以下因素而降低：

1. 采样率不足：低采样率会导致高频信息丢失。
2. 量化精度低：低比特深度会增加量化噪声。
3. 有损压缩：如 MP3 等格式，会丢弃部分音频信息。
4. 不精确的信号处理：在变换和处理过程中引入的误差会影响音质。

3.2 频域转音频

通过傅立叶逆变换实现

• 幅度+相位: 可以还原音频

# 提取幅度谱和相位谱
magnitude = np.abs(D)
phase = np.angle(D)

# 重构复数频域信号
reconstructed_D = magnitude * np.exp(1j * phase)

# 进行逆短时傅里叶变换 (ISTFT)
reconstructed_y = librosa.istft(reconstructed_D)

• 只有幅度: 部分还原音频

但丢失相位信息，需要估计重建，线性还原音质较差

从梅尔频谱图恢复音频信号代码：

# Step 1: 将梅尔频谱图转换回线性频谱图
mel_basis = librosa.filters.mel(sr=sr, n_fft=2048, n_mels=128)
mel_to_linear = np.dot(np.linalg.pinv(mel_basis), mel_spectrogram)

# Step 2: 使用 Griffin-Lim 算法从线性频谱图恢复音频
recovered_audio = librosa.feature.inverse.griffinlim(mel_to_linear) 

由于梅尔频谱图和频谱图通常只包含幅度信息，恢复音频信号时必须估计相位信息。
Griffin-Lim 算法通过迭代优化来逼近真实的相位，还原后音质较差。

• 只有相位: 还原音频难度极大

有两种简单的方法：

magnitude = np.ones_like(phase) # 假设所有波的幅值为1
magnitude = np.random.random(phase.shape) # 为所有波生成随机幅度

# 重构复数频域信号
reconstructed_D = magnitude * np.exp(1j * phase)

# 进行逆短时傅里叶变换 (ISTFT)
reconstructed_y = librosa.istft(reconstructed_D)

测试发现，还原的音频基本是噪声或不相关的音频内容

所以，无论是 假设所有波的固定幅度，还是为所有波生成随机幅度，相位谱都无法还原原有音频特征。

4.案例代码

如果想测试自己的音频与图谱转换，或可视化文中的频谱图，相关代码放在github：d_code