单调栈：柱形统计图中最大面积（POJ 2559）

题目大意：

给出一个柱形统计图(histogram), 它的每个项目的宽度是1， 高度和具体问题有关。 现在编程求出在这个柱形图中的最大面积的长方形。

例如： 

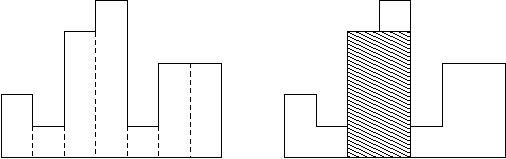
7 2 1 4 5 1 3 3

 

7表示柱形图有7个数据，分别是 2 1 4 5 1 3 3， 对应的柱形图如下，最后求出来的面积最大的图如右图所示。

 

一开始又是各种挫计O(n^2)，隐约感觉可以利用以前的某道题目的思想，然后，然后还是记不起来。。。

各种整之后，还是省点时间吧~ ⊙﹏⊙b ；

关键字：“单调栈” 感觉凉风一阵，什么情况，从没有见过的数据结构。赶紧上google百度之：

定义：

单调栈，顾名思义就是说栈内的元素，按照某种方式排序下，必须是单调的。如果新入栈的元素破坏了单调性，就弹出栈内元素，知道满足单调性。

它可以很方便地求出某个数的左边或者右边第一个比它大或者小的元素，而且总时间复杂度O(N)。

看完这里更加确定我见过类似的题目，但还是想不起来。其实也没见得是什么新的数据结构，只不过利用这个思想应该可以解决一大票问题，不信问ACMers就知道了。这个我们不关心，还是好好看看题目怎么做吧！

挫计的方法就不说了，直接进入主题，当然是循序渐进。。。

试想：

要想找到里面的最大的面积，一定会有这么一种情况，得出的矩形的高度一定为所包含的某一个高度一致的。所以我们可以对某一个柱子的高度为标准，尽量的向两头扩展，这样就可以找出以它高度为标准的，并包含它本身的最大矩形。然后对每一个柱子都做类似的工作，最后挑出里面最大的矩形。

OK，单从上述所说，一定会有重复的工作，如何剔除重复工作呢？而且什么叫做尽量向两头扩展呢？

重复工作之后再说。先说什么叫尽量向两头扩展。

如：2 1 4 

第一个：2，以2为高度为准，向左右两头扩展，它只能想右扩展，因为1比2低了，就不可能扩展到1了。宽度只有1。

第二个：1，以1为高度为准，向左右两头扩展，向左，因为2比1高可以扩展过去；向右，因为4也高于1所以扩展到4，这样以1为高度的矩形宽为3了；

第三个：4，以4为高度为准，向左右两头扩展，向左，因为4比1、2都高，显然不可以扩展过去，这样以4为高度的矩形宽为1了。

所以要将其扩展过去，必须高度高于当前扩展点的高度。

所以如果我们从第一个开始计算到第n个，计算到i时，如果我们可以快速的找出左边第一个（这里第一的意思是离i最近）的比i的高度小的，就可以完成了向左扩展的工作，而向右扩展，我们本来就是一直向右走，所以直接扩展。这时候就轮到：单调栈出场了！

一直保持单调递增的栈。

思考刚才的例子：

2进栈，左边无比其小的元素，记录其最左扩展位置为1

1准备进栈，因为其进栈就破坏了单调栈的性质（2>1），这时2要出栈，因为1<2也说明了2不可能向右扩展，出栈，计算以2为准的矩形 2*1，然后1才进栈。1进栈前，发现其前一个元素，既是当前的栈顶2，比1高，而且2的左扩展从位置1开始，所以1也有理由从2的左起始位置开始（注意：2比1高），所以2出栈后，1进栈，其左扩展应为2的左扩展位置1；

4准备进栈，因为4>1直接进栈，其左扩展位置只能为3了。

最后要清空栈：4退栈，以为是最右的了，这此时右扩展只能为3了。左右扩展都为3，即是其本身，矩形为4*1；记录其位置以备后需；

1退栈，最右扩展只能是上一个退栈的元素位置，因为其高度比1高（单调栈的性质），所以利用刚才记录的位置，1的左右扩展就为1，3了，矩形1*3；

完成。

例子过于简单不能描述算法，只能感受其中思想。多说无益，直接上码：

 

 1 #include <iostream>

 2 #include <stack>

 3 

 4 using namespace std;

 5 

 6 typedef struct _Pillar

 7 {

 8     int heigt;

 9     int left;

10 }Pillar;

11 

12 int func29(int a[], int n)

13 {

14     stack<Pillar> st;

15 

16     Pillar tmp,p;

17     Pillar pzero ={-1, 0};

18     st.push(pzero);

19     int maxs=0;

20     int squ;

21 

22     for (int i=0; i<n; ++i)

23     {

24         tmp  = st.top();

25         

26         if(tmp.heigt >= a[i])

27         {

28             

29             while(tmp.heigt> a[i])  //Note: 不相等

30             {

31                 squ = tmp.heigt*(i-tmp.left);

32                 maxs = squ>maxs ? squ : maxs;

33                 cout<<"Height"<<tmp.heigt<<":"<<squ<<endl;

34                 st.pop();

35                 tmp = st.top();

36             }

37             p.heigt = a[i];

38             p.left = tmp.left;

39 

40             st.push(p);

41         }

42         else 

43         {

44             p.heigt = a[i];

45             p.left = i;

46             st.push(p);

47         }

48 

49     }

50 

51 

52     while(!st.empty())

53     {

54         tmp = st.top();

55         if (tmp.heigt != -1)

56         {

57             squ = tmp.heigt*(i-tmp.left);

58             maxs = squ>maxs ? squ : maxs;

59             cout<<"Height"<<tmp.heigt<<":"<<squ<<endl;

60         }        

61         st.pop();

62     }

63 

64     return maxs;

65 }

66 int main()

67 {    

68     int a2[]={2 ,1 ,4,5 ,1,3,3};

69 

70     cout<<"Max :"<<func29(a2, sizeof(a2)/sizeof(int))<<endl;

71 

72 

73 

74     

75     return 0;

76 }

 

终于回想起过去的那一道题目，也是利用这个思想的：谁看得最大 ，那里没有使用栈，要数组模拟了单调栈，当然这一题也可以这么做。

毕