重心坐标 笛卡尔坐标
书到用时方恨少,今天看别人源码的时候一下看不懂了,故写文章mark之
引用维基链接: http://zh.wikipedia.org/zh-cn/%E9%87%8D%E5%BF%83%E5%9D%90%E6%A0%87
首先,我卡在
从而 
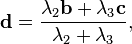这里非常久,实在看不懂,想不通怎么是这个比列,这也从某个方面说出了问题,想了半天,自己动笔一算,设BD:DC = x:y,然后根据面积比 (注意,利用共高)
S△abd / S△adc = x/y 而λ1 +λ2 +λ3 = 1;下面面积也等于x/y故 S△pad =(1-λ2 -λ3)* x/(x+y) 同理 S△pdc = (1-λ2 -λ3)* y/(x+y)
S △abd = λ3 + S△pad 同理 S△adc =λ2 + S△pdc 比之即可得出 x/y =λ3 : λ2
至于
显然 区间[a,b],求d(x/y)的坐标 为: 总共为x+y分,平分为1/x+y 那么d的坐标 = a + x/(x+y) * (b-a)
至于
同理利用面积比 ,设AP:PD = z:w ,即为S△apc / S△cpd(共高) S△apc = λ2 S△pdc = (1-λ2 -λ3)* y/(x+y) =λ1 *λ2 / (λ2 +λ3)
得到z:w = (λ2 +λ3) : λ1
同理得到: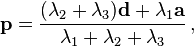 
那么有两种转换,第一种从 重心坐标到笛卡尔坐标: 这部分参照维基即可:
故
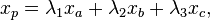和
第二种,从笛卡尔坐标到重心坐标,要求面积比,我蛋疼了半天2D的三角形面积,主要是把他当成3D中的三角形来求了
首先3D中的三角形等于X乘,展开X乘得到(假设一个点在原点设P0(0,0,0)P1(x1,y1,z1)P2(x2,y2,z2))
按规定，有：单位向量的模为
可得叉积的模为：
|P1×P2| = y1z2 - y2z1 + x2z1 - x1z2 + x1y2 - x2y1
= (y1z2 + x2z1 + x1y2) - (y2z1 + x1z2 + x2y1)
然后不在原点平移过去即可
|B×C| =
| 1 1 1 |
= |x1-x0 y1-y0 z1-z0|
|x2-x0 y2-y0 z2-z0|
注意2D中没有z分量,令之等于0,故得到2D中的面积公式: (x1-x0)*(y2-y0)-(x2-x0)*(y1-y0)
求得面积只需要求出两个比值即可 ,因为总和等于 1,注意有可能是负数,当点在三角形外
Mark完毕,代码编写时需要保持一定的一致性,否则会让人产生困惑,以及使用中间变量便于理解,不要写长式,
像这种写法,尽管 /=的是相同东西,但是一样看过去不是一样的,需要警戒这种情况
以及加上注释说明使用的数学公式