局域网电脑感染(华为od机考题)
一、题目
1.原题
一个局域网内有很多台电脑,分别标注为0 - N-1的数字。相连接的电脑距离不一样,所以感染时间不一样,感染时间用t表示。
其中网络内一个电脑被病毒感染,其感染网络内所有的电脑需要最少需要多长时间。如果最后有电脑不会感染,则返回-1;
给定一个数组times表示一个电脑把相邻电脑感染所用的时间。
如图:path[i]= {i,j, t} 表示电脑i->j 电脑i上的病毒感染j,需要时间t。
2.题目理解
考点:图
二、思路与代码过程
1.思路
Dijkstra算法
2.算法核心讲解
eg:
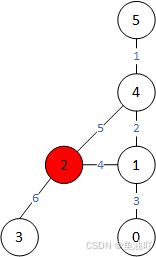
假设该局域网内有n=6台电脑,电脑间的连接数为m=6(即有6个点,6条边);
path[i]= {i,j, t}表示从i点传染到j点所需要的时间;
int n = 6; int m = 6;
int[][] path = {{3, 2, 6}, {2, 1, 4}, {2, 4, 5}, {1, 0, 3}, {1, 4, 2}, {4, 5, 1}};
如图设起点为2,要求其感染网络内所有的电脑需要最少需要多长时间,用到Dijkstra算法。
先将path数组输入graph(边Edge:顶点from +邻接点to+感染时间time);
graph:
[vertice:0,edge:[1,3]]
[vertice:1,edge:[2,4], vertice:1,edge:[0,3], vertice:1,edge:[4,2]]
[vertice:2,edge:[3,6], vertice:2,edge:[1,4], vertice:2,edge:[4,5]]
[vertice:3,edge:[2,6]]
[vertice:4,edge:[2,5], vertice:4,edge:[1,2], vertice:4,edge:[5,1]]
[vertice:5,edge:[4,1]]
新建一个dist[]数组用于记录从起点到i点的耗时(dist[i]表示从起点到i点的累计用时),该数组全部初始化为最大值;
新建一个优先队列,存储节点i和该节点的用时(dist[i]),最初放入起点start和时间0;
进入循环遍历找时间:
从pq队列中拿一个元素(节点,时间),根据图graph对当前节点的边进行遍历:
---------------------------------------------------------------------------------------------------------------------------------
eg:开始pq:{2,0}
当前dist[]={Integer.MAX_VALUE,Integer.MAX_VALUE,0,Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE};
节点为2,从graph找到顶点为2的边:
edge:[3,6], edge:[1,4],edge:[4,5]
当当前dist[相邻节点]的值大于dist[当前节点]+感染时间:
(比如最开始dist[]数组全部初始化为最大值,第一次遍历到就会更新)
对dist[相邻节点]赋值:
dist[3]=dist[2]+time=0+6=6;
dist[1]=dist[2]+time=0+4=4;
dist[4]=dist[2]+time=0+5=5;
判断:
dist[3]=6
dist[1]=4
dist[4]=5
当前dist[]={Integer.MAX_VALUE,4,0,6,5,Integer.MAX_VALUE};
将节点与时间加入pq;
当前pq:{{1,4},{4,5},{3,6}}(pq根据数组的第二个元素时间进行排序)
---------------------------------------------------------------------------------------------------------------------------------
下一次循环:
从pq中取出:节点为1,dist[1]=4;
从graph找到顶点为1的边:
edge:[2,4], edge:[0,3],edge:[4,2]
对dist[相邻节点]赋值:
dist[2]=dist[1]+time=4+4=8,
dist[0]=dist[1]+time=4+3=7,
dist[4]=dist[1]+time=4+2=6;
判断:
dist[2]=8>0;×
dist[0]=7
dist[4]=6>5;×
当前dist[]={7,4,0,6,5,Integer.MAX_VALUE};
将节点与时间加入pq;
当前pq:{{4,5},{3,6},{0,7}}(pq根据数组的第二个元素时间进行排序)
---------------------------------------------------------------------------------------------------------------------------------
下一次循环:
从pq中取出:节点为4,dist[4]=5;
从graph找到顶点为4的边:
edge:[2,5], edge:[1,2], edge:[5,1]
对dist[相邻节点]赋值:
dist[2]=dist[4]+time=5+5=10;
dist[1]=dist[4]+time=5+2=7;
dist[5]=dist[4]+time=5+1=6;
判断:
dist[2]=10>0;×
dist[1]=7>4;×
dist[5]=6
当前dist[]={7,4,0,6,5,6};
将节点与时间加入pq;
当前pq:{{3,6},{5,6},{0,7}}(pq根据数组的第二个元素时间进行排序)
---------------------------------------------------------------------------------------------------------------------------------
下一次循环:
从pq中取出:节点为3,dist[3]=6;
从graph找到顶点为3的边:
edge:[2,6]
对dist[相邻节点]赋值:
dist[2]=dist[3]+time=6+6=12;
判断:
dist[2]=12>0;×
当前dist[]={7,4,0,6,5,6};
将节点与时间加入pq;
当前pq:{{5,6},{0,7}}(pq根据数组的第二个元素时间进行排序)
---------------------------------------------------------------------------------------------------------------------------------
下一次循环:
从pq中取出:节点为5,dist[5]=6;
从graph找到顶点为5的边:
edge:[4,1]
对dist[相邻节点]赋值:
dist[4]=dist[5]+time=6+1=7;
判断:
dist[4]=7>5;×
当前dist[]={7,4,0,6,5,6};
无节点与时间加入pq;
当前pq:{{0,7}}(pq根据数组的第二个元素时间进行排序)
---------------------------------------------------------------------------------------------------------------------------------
下一次循环:
从pq中取出:节点为0,dist[0]=7;
从graph找到顶点为0的边:
edge:[1,3]
对dist[相邻节点]赋值:
dist[1]=dist[0]+time=7+3=10;
判断:
dist[1]=10>7;×
当前dist[]={7,4,0,6,5,6};
无节点与时间加入pq;
当前pq:{}(pq根据数组的第二个元素时间进行排序)
---------------------------------------------------------------------------------------------------------------------------------
循环结束
当前dist[]={7,4,0,6,5,6};
用Arrays.stream(dist).max().getAsInt();
找出dist数组中的最大数就是感染网络内所有的电脑最少需要的时间(在所有节点时间积累量最小的基础上遍历完全部图)。
(若最后dist中仍存在值等于Integer.MAX_VALUE,那么就存在电脑无法被感染,返回-1)
得出最少感染用时为7。
3.代码过程
①main函数
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println("请输入该局域网内的电脑数目:");
int n = sc.nextInt();
System.out.println("请输入该局域网中电脑间的链接数:");
int m = sc.nextInt();
System.out.println("请输入该局域网中电脑感染相邻电脑所需时间的数组path-times:");
int[][] path = new int[m][3];
for (int i = 0; i < m; i++) {
for (int j = 0; j < 3; j++) {
path[i][j] = sc.nextInt();
}
}
System.out.println("请输入第一台被感染的电脑编号:");
int start = sc.nextInt();
//转存入图表
List> graph = new ArrayList<>();
graph = ToGraph(path);
int t = TimeCal(graph,start);
System.out.println("最短感染时间为:"+t);
} ②TimeCal函数
private static int TimeCal(List> graph, int start) {
//graph图的结构:vertice顶点 + edge(to相邻节点+time所需时间),顶点数量与图大小相同
//dist[i]表示从起点start到当前i顶点所用的最短时间
//状态累积
int[] dist = new int[graph.size()];
//初始化dist为最大时间
Arrays.fill(dist, Integer.MAX_VALUE);
//初始化起点到起点的时间为0
dist[start] = 0;
//初始化一个优先队列
PriorityQueue pq = new PriorityQueue<>
(Comparator.comparingInt(a -> a[1]));
pq.add(new int[]{start,0});
//pq:{2,0}
/*Dijkstra算法*/
while (!pq.isEmpty()) {
//获取当前节点和时间(除了起点都来自dist[])
int[] curNT = pq.poll();
int curN = curNT[0];
int curT = curNT[1];
//若当前时间大于该节点已有时间,则跳过后序
if (curT>dist[curN]) {
continue;
}
//遍历当前节点的所有边edge
for (Edge edge : graph.get(curN)) {
//将当前节点的相邻节点和需要时间赋值
int destN = edge.to;
int timeS =edge.time;
//对dist[下一个节点]赋值,并保持最小
if (dist[destN]+timeS ③ToGraph函数
private static List> ToGraph(int[][] path) {
//先找所有节点,将节点存入list
Set Node = new HashSet<>();
for (int[] i : path) {
Node.add(i[0]);
Node.add(i[1]);
}
List nodeList = new ArrayList<>(Node);
List> graph = new ArrayList<>();
for (int i = 0;i < Node.size();i++) {
graph.add(new ArrayList<>());
}
//再将所有节点Node与to,time对应,无向图(双向)
for (int i = 0;i < Node.size();i++) {
int node = nodeList.get(i);
for (int[] line : path) {
if (line[0] == node) {
int neighbor = line[1];
int time = line[2];
Edge edge = new Edge(node,neighbor,time);
graph.get(node).add(edge);
}else if (line[1] == node) {
int neighbor = line[0];
int time = line[2];
Edge edge = new Edge(node,neighbor,time);
graph.get(node).add(edge);
}
}
return graph;
} ④Edge类
(可以不定义直接写一个ArrayList
public static class Edge{
int from;
int to;
int time;
public Edge(int from,int to, int time){
this.from = from;
this.to = to;
this.time = time;
}
public String toString(){
return "vertice:"+from+",edge:["+to+","+time+"]";
}
}三、运行结果
1.运行截图
2.带数据分析运行结果
请输入该局域网内的电脑数目:
6
请输入该局域网中电脑间的链接数:
6
请输入该局域网中电脑感染相邻电脑所需时间的数组path-times:
3 2 6
2 1 4
2 4 5
1 0 3
1 4 2
4 5 1
[[3, 2, 6], [2, 1, 4], [2, 4, 5], [1, 0, 3], [1, 4, 2], [4, 5, 1]]
请输入第一台被感染的电脑编号:
2
Node表:[0, 1, 2, 3, 4, 5]
[0, 1, 2, 3, 4, 5]
初始化:[[], [], [], [], [], []]
edge[1]:0,与当前顶点值相等。
他的邻居为:1,当前边所需时间为:3
vertice:0,edge:[1,3]
[vertice:0,edge:[1,3]]
[]
[]
[]
[]
[]
edge[1]:1,与当前顶点值相等。
他的邻居为:2,当前边所需时间为:4
vertice:1,edge:[2,4]
edge[0]:1,与当前顶点值相等。
他的邻居为:0,当前边所需时间为:3
vertice:1,edge:[0,3]
edge[0]:1,与当前顶点值相等。
他的邻居为:4,当前边所需时间为:2
vertice:1,edge:[4,2]
[vertice:0,edge:[1,3]]
[vertice:1,edge:[2,4], vertice:1,edge:[0,3], vertice:1,edge:[4,2]]
[]
[]
[]
[]
edge[1]:2,与当前顶点值相等。
他的邻居为:3,当前边所需时间为:6
vertice:2,edge:[3,6]
edge[0]:2,与当前顶点值相等。
他的邻居为:1,当前边所需时间为:4
vertice:2,edge:[1,4]
edge[0]:2,与当前顶点值相等。
他的邻居为:4,当前边所需时间为:5
vertice:2,edge:[4,5]
[vertice:0,edge:[1,3]]
[vertice:1,edge:[2,4], vertice:1,edge:[0,3], vertice:1,edge:[4,2]]
[vertice:2,edge:[3,6], vertice:2,edge:[1,4], vertice:2,edge:[4,5]]
[]
[]
[]
edge[0]:3,与当前顶点值相等。
他的邻居为:2,当前边所需时间为:6
vertice:3,edge:[2,6]
[vertice:0,edge:[1,3]]
[vertice:1,edge:[2,4], vertice:1,edge:[0,3], vertice:1,edge:[4,2]]
[vertice:2,edge:[3,6], vertice:2,edge:[1,4], vertice:2,edge:[4,5]]
[vertice:3,edge:[2,6]]
[]
[]
edge[1]:4,与当前顶点值相等。
他的邻居为:2,当前边所需时间为:5
vertice:4,edge:[2,5]
edge[1]:4,与当前顶点值相等。
他的邻居为:1,当前边所需时间为:2
vertice:4,edge:[1,2]
edge[0]:4,与当前顶点值相等。
他的邻居为:5,当前边所需时间为:1
vertice:4,edge:[5,1]
[vertice:0,edge:[1,3]]
[vertice:1,edge:[2,4], vertice:1,edge:[0,3], vertice:1,edge:[4,2]]
[vertice:2,edge:[3,6], vertice:2,edge:[1,4], vertice:2,edge:[4,5]]
[vertice:3,edge:[2,6]]
[vertice:4,edge:[2,5], vertice:4,edge:[1,2], vertice:4,edge:[5,1]]
[]
edge[1]:5,与当前顶点值相等。
他的邻居为:4,当前边所需时间为:1
vertice:5,edge:[4,1]
[vertice:0,edge:[1,3]]
[vertice:1,edge:[2,4], vertice:1,edge:[0,3], vertice:1,edge:[4,2]]
[vertice:2,edge:[3,6], vertice:2,edge:[1,4], vertice:2,edge:[4,5]]
[vertice:3,edge:[2,6]]
[vertice:4,edge:[2,5], vertice:4,edge:[1,2], vertice:4,edge:[5,1]]
[vertice:5,edge:[4,1]]
当前节点:2,当前节点的时间:0
当前节点:vertice:2,edge:[3,6]
当前节点:vertice:2,edge:[1,4]
当前节点:vertice:2,edge:[4,5]
当前节点:1,当前节点的时间:4
当前节点:vertice:1,edge:[2,4]
当前节点:vertice:1,edge:[0,3]
当前节点:vertice:1,edge:[4,2]
当前节点:4,当前节点的时间:5
当前节点:vertice:4,edge:[2,5]
当前节点:vertice:4,edge:[1,2]
当前节点:vertice:4,edge:[5,1]
当前节点:3,当前节点的时间:6
当前节点:vertice:3,edge:[2,6]
当前节点:5,当前节点的时间:6
当前节点:vertice:5,edge:[4,1]
当前节点:0,当前节点的时间:7
当前节点:vertice:0,edge:[1,3]
[7, 4, 0, 6, 5, 6]
最短感染时间为:7
3.带数据分析完整代码
import java.util.*;
public class test27 {
/*
一个局域网内有很多台电脑,分别标注为0 - N-1的数字。
相连接的电脑距离不一样,所以感染时间不一样,感染时间用t表示。
其中网络内一个电脑被病毒感染,其感染网络内所有的电脑需要最少需要多长时间。
如果最后有电脑不会感染,则返回-1。
给定一个数组times表示一个电脑把相邻电脑感染所用的时间。
如图:path[i]= {i,j, t} 表示电脑i->j 电脑i上的病毒感染j,需要时间t。
*/
public static void main(String[] args) {
/*
Scanner sc = new Scanner(System.in);
System.out.println("请输入该局域网内的电脑数目:");
int n = sc.nextInt();
System.out.println("请输入该局域网中电脑间的链接数:");
int m = sc.nextInt();
System.out.println("请输入该局域网中电脑感染相邻电脑所需时间的数组path-times:");
int[][] path = new int[m][3];
for (int i = 0; i < m; i++) {
for (int j = 0; j < 3; j++) {
path[i][j] = sc.nextInt();
}
}
System.out.println(Arrays.deepToString(path));
System.out.println("请输入第一台被感染的电脑编号:");
int start = sc.nextInt();
int t = TimeCal(path,v);
System.out.println("最短感染时间为:"+t);
*/
/*简单测试
int n = 4;
int m = 3;
int[][] path = {{1, 0, 1}, {1, 2, 1}, {2, 3, 1}};
System.out.println(Arrays.deepToString(path));
int start =2;
*/
/*复杂测试*/
int n = 6;
int m = 6;
int[][] path = {{3, 2, 6},
{2, 1, 4},
{2, 4, 5},
{1, 0, 3},
{1, 4, 2},
{4, 5, 1}};
System.out.println(Arrays.deepToString(path));
int start =2;
//转存入图表
List> graph = new ArrayList<>();
graph = ToGraph(path);
//System.out.println("main中的图:"+graph);
int t = TimeCal(graph,start);
System.out.println("最短感染时间为:"+t);
}
private static int TimeCal(List> graph, int start) {
//graph图的结构:vertice顶点 + edge(to相邻节点+time所需时间),顶点数量与图大小相同
//dist[i]表示从起点start到当前i顶点所用的最短时间
//状态累积
int[] dist = new int[graph.size()];
//初始化dist为最大时间
Arrays.fill(dist, Integer.MAX_VALUE);
//初始化起点到起点的时间为0
dist[start] = 0;
//初始化一个优先队列
PriorityQueue pq = new PriorityQueue<>
(Comparator.comparingInt(a -> a[1]));
pq.add(new int[]{start,0});
//pq:{2,0}
/*Dijkstra算法*/
while (!pq.isEmpty()) {
//获取当前节点和时间(除了起点都来自dist[])
int[] curNT = pq.poll();
int curN = curNT[0];
int curT = curNT[1];
System.out.println("当前节点:"+curN+",当前节点的时间:"+curT);
//若当前时间大于该节点已有时间,则跳过后序
if (curT>dist[curN]) {
continue;
}
//遍历当前节点的所有边edge
for (Edge edge : graph.get(curN)) {
System.out.println("当前节点:"+edge);
//将当前节点的相邻节点和需要时间赋值
int destN = edge.to;
int timeS =edge.time;
//对dist[下一个节点]赋值,并保持最小
if (dist[destN]+timeS> ToGraph(int[][] path) {
//先找所有节点,将节点存入list
Set Node = new HashSet<>();
for (int[] i : path) {
Node.add(i[0]);
Node.add(i[1]);
}
System.out.print("Node表:");
System.out.println(Node);//
List nodeList = new ArrayList<>(Node);
System.out.println(nodeList);//
List> graph = new ArrayList<>();
for (int i = 0;i < Node.size();i++) {
graph.add(new ArrayList<>());
}
System.out.println("初始化:"+graph+"\n");
//再将所有节点Node与to,time对应,无向图(双向)
for (int i = 0;i < Node.size();i++) {
int node = nodeList.get(i);
for (int[] line : path) {
if (line[0] == node) {
System.out.println("edge[0]:"+line[0]+",与当前顶点值相等。");
System.out.println("他的邻居为:"+line[1]+",当前边所需时间为:"+line[2]);
int neighbor = line[1];
int time = line[2];
Edge edge = new Edge(node,neighbor,time);
graph.get(node).add(edge);
System.out.println(edge);
}else if (line[1] == node) {
System.out.println("edge[1]:"+line[1]+",与当前顶点值相等。");
System.out.println("他的邻居为:"+line[0]+",当前边所需时间为:"+line[2]);
int neighbor = line[0];
int time = line[2];
Edge edge = new Edge(node,neighbor,time);
graph.get(node).add(edge);
System.out.println(edge);
}
}
for (List edge : graph) {
System.out.println(edge);
}
System.out.println();
}
return graph;
}
public static class Edge{
int from;
int to;
int time;
public Edge(int from,int to, int time){
this.from = from;
this.to = to;
this.time = time;
}
public String toString(){
return "vertice:"+from+",edge:["+to+","+time+"]";
}
}
}