绪论:加法原理、乘法原理#
分类计数原理:做一件事,有 n n 类办法,在第 1 1 类办法中有 m1 m 1 种不同的方法,在第 2 2 类办法中有 m2 m 2 种不同的方法,…,在第 n n 类办法中有 mn m n 种不同的方法,那么完成这件事共有 N=m1+m2+…+mn N = m 1 + m 2 + … + m n 种不同的方法。
分步计数原理:完成一件事,需要分成 n n 个步骤,做第 1 1 步有 m1 m 1 种不同的方法,做第 2 2 步有 m2 m 2 种不同的方法,…,做第 n n 步有 mn m n 种不同的方法,那么完成这件事共有 N=m1×m2×⋯×mn N = m 1 × m 2 × ⋯ × m n 种不同的方法。
区别:分类计数原理是加法原理,不同的类加起来就是我要得到的总数;分步计数原理是乘法原理,是同一事件分成若干步骤,每个步骤的方法数相乘才是总数。
排列问题#
排列数#
从 n n 个不同元素种取出 m(m≤n) m ( m ≤ n ) 个元素的所有不同排列的个数,叫做从 n n 个不同元素种取出 m m 个元素的排列数,用符号 Amn A n m 表示。
排列数公式#
(规定 0!=1 0 ! = 1 )
推导:把 n n 个不同的元素任选 m m 个排序,按计数原理分步进行:
取第一个:有 n n 种取法;
取第二个:有 (n−1) ( n − 1 ) 种取法;
取第三个:有 (n−2) ( n − 2 ) 种取法;
……
取第 m m 个:有 (n−m+1) ( n − m + 1 ) 种取法;
根据分步乘法原理,得出上述公式。
排列数性质#
Amn=nAm−1n−1 A n m = n A n − 1 m − 1 可理解为“某特定位置”先安排,再安排其余位置。
Amn=mAm−1n−1+Amn−1 A n m = m A n − 1 m − 1 + A n − 1 m 可理解为:含特定元素的排列有 mAm−1n−1 m A n − 1 m − 1 ,不含特定元素的排列为 Amn−1 A n − 1 m 。
组合问题#
组合数#
从 n n 个不同元素种取出 m(m≤n) m ( m ≤ n ) 个元素的所有不同组合的个数,叫做从 n n 个不同元素种取出 m m 个元素的组合数,用符号 Cmn C n m 表示。
组合数公式#
证明:利用排列和组合之间的关系以及排列的公式来推导证明。
将部分排列问题 Amn A n m 分解为两个步骤:
第一步,就是从 n n 个球中抽 m m 个出来,先不排序,此即组合数问题 Cmn C n m ;
第二步,则是把这 m m 个被抽出来的球排序,即全排列 Amm A m m 。
根据乘法原理, Amn=CmnAmm A n m = C n m A m m ,那么
组合数的性质#
Cmn=Cn−mn C n m = C n n − m 可以理解为:将原本的每个组合都反转,把原来没选的选上,原来选了的去掉,这样就变成从 n n 个元素种取出 n−m n − m 个元素,显然方案数是相等的。
递推公式 Cmn=Cmn−1+Cm−1n−1 C n m = C n − 1 m + C n − 1 m − 1 可理解为:含特定元素的组合有 Cm−1n−1 C n − 1 m − 1 ,不含特定元素的排列为 Cmn−1 C n − 1 m 。还不懂?看下面。
Example
从1,2,3,4,5( n=5 n = 5 )中取出2( m=2 m = 2 )个元素的组合( Cmn C n m ):
12 13 14 15 23 24 25 34 35 45
显然,这些组合中要么含有元素“1”,要么不含。
-
其中含有“1”的是:12 13 14 15
把里面的“1”都挖掉:2 3 4 5
而上面这个等价于从2,3,4,5( n−1 n − 1 )中取出1( m−1 m − 1 )个元素的组合。
-
其中不含“1”的是:23 24 25 34 35 45
上面等价于从2,3,4,5( n−1 n − 1 )中取出2( m m )个元素的组合。
而总方案数等于上面两种情况方案数之和,即 Cmn=Cmn−1+Cm−1n−1 C n m = C n − 1 m + C n − 1 m − 1 。
组合数求和公式#
我们感性认知一下,上面这个式子的左边表示什么呢?
把从 n n 个球中抽出 0 0 个球的组合数(值为 1 1 )、抽出 1 1 个球的组合数、抽出 2 2 个球的组合数、……、抽出 n n 个球的组合数相加。
换句话说,就是从 n n 个球中随便抽出一些不定个数球,问一共有多少种组合。
对于第1个球,可以选,也可以不选,有2种情况。
对于第2个球,可以选,也可以不选,有2种情况。
对于任意一个球,可以选,也可以不选,有2种情况。
根据乘法原理,一共 2×2×⋯×2n个2相乘=2n 2 × 2 × ⋯ × 2 ⏟ n 个2相乘 = 2 n 种组合。
想要严谨的证明?数学归纳法:
- 当 n=1 n = 1 时, C01+C11=2=21 C 1 0 + C 1 1 = 2 = 2 1 成立。
- 假设 n=k(k∈N∗) n = k ( k ∈ N ∗ ) 时等式成立,即
n=k+1 n = k + 1 时,∑i=0kCik=2n ∑ i = 0 k C k i = 2 n====C0k+1+C1k+1+C2k+1+⋯+Ckk+1+Ck+1k+1C0k+1+(C0k+C1k)+(C1k+C2k)+⋯+(Ck−1k+Ckk)+Ck+1k+1(C0k+C1k+C2k+⋯+Ckk)+(C0k+C1k+C2k+⋯+Ckk)2×2k2k+1 C k + 1 0 + C k + 1 1 + C k + 1 2 + ⋯ + C k + 1 k + C k + 1 k + 1 = C k + 1 0 + ( C k 0 + C k 1 ) + ( C k 1 + C k 2 ) + ⋯ + ( C k k − 1 + C k k ) + C k + 1 k + 1 = ( C k 0 + C k 1 + C k 2 + ⋯ + C k k ) + ( C k 0 + C k 1 + C k 2 + ⋯ + C k k ) = 2 × 2 k = 2 k + 1
- 由1、2得,等式对 n∈N∗ n ∈ N ∗ 都成立。
也可偷懒地用二项式定理证明:
令 a=b=1 a = b = 1 ,就得到了
类似的公式(由 Cmn=Cn−mn C n m = C n n − m 推导):
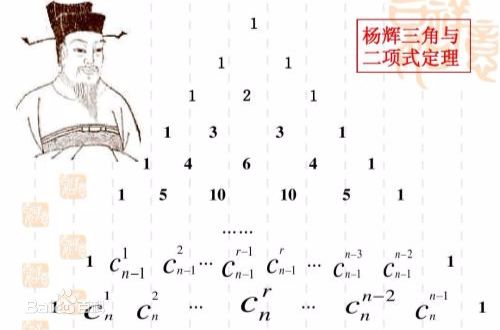
杨辉三角#
这个神奇的图形和组合数、二项式定理密切相关。(图片来自百度百科)
杨辉三角可以帮助你更好地理解和记忆组合数的性质:
- 第 n n 行的 m m 个数可表示为 Cm−1n−1 C n − 1 m − 1 ,即为从 n−1 n − 1 个不同元素中取 m−1 m − 1 个元素的组合数。
- 第 n n 行的数字有 n n 项。
- 每行数字左右对称(第 n n 行的第 m m 个数和第 n−m+1 n − m + 1 个数相等, Cmn=Cn−mn C n m = C n n − m ),由 1 1 开始逐渐变大。
- 每个数等于它上方两数之和(第 n+1 n + 1 行的第 i i 个数等于第 n n 行的第 i−1 i − 1 个数和第 i i 个数之和,即 Cin+1=Cin+Ci−1n C n + 1 i = C n i + C n i − 1 )。
- (a+b)n ( a + b ) n 的展开式中的各项系数依次对应杨辉三角的第 n+1 n + 1 行中的每一项(二项式定理)。
以下来自维基百科(我只是随便贴这)
二项式系数
二项式系数可排列成帕斯卡三角形。
在数学上,二项式系数是二项式定理中各项的系数。一般而言,二项式系数由两个非负整数 n n 和 k k 为参数决定,写作,定义为的多项式展开式中,项的系数,因此一定是非负整数。如果将二项式系数写成一行,再依照顺序由上往下排列,则构成帕斯卡三角形。 (nk)(1+x)nxk(n0),(n1),…,(nn)n=0,1,2,… ( n k ) ( 1 + x ) n x k ( n 0 ) , ( n 1 ) , … , ( n n ) n = 0 , 1 , 2 , …
二项式系数常见于各数学领域中,尤其是组合数学。事实上,可以被理解为从 n n 个相异元素中取出 k k 个元素的方法数,所以大多读作「 n n 取 k k 」。二项式系数的定义可以推广至 n n 是复数的情况,而且仍然被称为二项式系数。
二项式系数亦有不同的符号表达方式,包括: C(n,k) C ( n , k ) 、 nCk n C k 、 nCk n C k 、、[注3],其中的C代表组合(combinations)或选择(choices)。很多计算机使用含有C的变种记号,使得算式只占一行的空间,相同理由也发生在置换数,例如写作 P(n,k) P ( n , k ) 。 CknCnkPnk C n k C k n P k n
定义及概念
对于非负整数 n n 和 k k ,二项式系数定义为的多项式展开式中,项的系数,即 (nk)(1+x)nxk ( n k ) ( 1 + x ) n x k
(1+x)n=∑k=0n(nk)xk=(n0)+(n1)x+⋯+(nn)xn ( 1 + x ) n = ∑ k = 0 n ( n k ) x k = ( n 0 ) + ( n 1 ) x + ⋯ + ( n n ) x n
事实上,若 x x 、 y y 为交换环上的元素,则
(x+y)n=∑nk=0(nk)xn−kyk ( x + y ) n = ∑ k = 0 n ( n k ) x n − k y k
此数的另一出处在组合数学,表达了从 n n 物中,不计较次序取 k k 物有多少方式,亦即从一 n n 元素集合中所能组成 k k 元素子集的数量。
计算二项式系数
除展开二项式或点算组合数量之外,尚有多种方式计算的值。 (nk) ( n k )
递归公式
以下递归公式可计算二项式系数:
(nk)=(n−1k−1)+(n−1k)∀n,k∈N ( n k ) = ( n − 1 k − 1 ) + ( n − 1 k ) ∀ n , k ∈ N
其中特别指定:
(n0)=1∀n∈N∪{0},(0k)=0∀k∈N ( n 0 ) = 1 ∀ n ∈ N ∪ { 0 } , ( 0 k ) = 0 ∀ k ∈ N .
此公式可由计算(1 + X ) n −1 (1 + X )中的X k项,或点算集合{1, 2, ..., n }的k个元素组合中包含n与不包含n的数量得出。
显然,如果k > n,则。而且对所有n,,故此上述递归公式可于此等情况下中断。递归公式可用作建构帕斯卡三角形。 \tbinom nk=0\tbinom nn=1
帕斯卡三角形(杨辉三角)
有关二项式系数的恒等式
关系式
阶乘公式能联系相邻的二项式系数,例如在k是正整数时,对任意n有:
两个组合数相乘可作变换:
主条目:朱世杰恒等式
二阶求和公式
主条目:范德蒙恒等式
三阶求和公式
主条目:李善兰恒等式