河南萌新联赛2024第(四)场:河南理工大学
河南萌新联赛2024第(四)场:河南理工大学
2024.8.7 13:00————17:00
过题数5/12
补题数8/12
- 该出奇兵了
- 小雷的神奇电脑
- 岗位分配
- 简单的素数
- AND
- 小雷的算式
- 循环字符串
- 聪明且狡猾的恶魔
- 马拉松
- 尖塔第四强的高手
- 比赛
- 抓字符
B - 小雷的神奇电脑
题解:
给出n个整数,保证他们的二进制位数小于m位,求数组中任意俩个数的同或最大值。
可以知道相邻俩个数同获最小,异或最大。
代码:
#include
using namespace std;
#define int long long
const int N = 2e5+10;
const int INF = 0x3f3f3f3f;
int a[N];
int qpow(int base,int power) {
int res = 1;
while(power) {
if(power & 1) res = res*base;
base = base*base;
power >>= 1;
}
return res;
}
signed main() {
int n,m;
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
sort(a+1,a+1+n);
int ans = 0;
int res = qpow(2,m)-1;
for (int i = 1;i <= n-1; i++) {
ans = max(a[i] xor a[i+1] xor res,ans);
}
cout << ans;
return 0;
}
C - 岗位分配
题解:
n个岗位,m位志愿者,每个岗位需要a[i]个志愿者,需要将志愿者分配到岗位上,可以有志愿者剩余。对分配情况计算总数,答案取模。岗位需求志愿者总和不超过志愿者个数,且志愿者间无差别。
分配问题,排列组合的隔板法。先把每个岗位需要的志愿者给他们,然后剩余的志愿者可以看作小球,分割到n个盒子里,可以有空盒子,剩余的志愿者也不用分配完,可以分配一个俩个多个等等。
代码:
#include
using namespace std;
#define int long long
const int mod = 998244353;
int qpow(int base,int power) {
int res = 1;
while(power) {
if(power & 1) res = res*base%mod;
base = base*base%mod;
power >>= 1;
}
return res;
}
int c(int x,int y) {
int res = 1;
for (int i = 1,j = x; i <= y; i++,j--) {
res=res*j%mod;
res = res*qpow(i,mod-2)%mod;
}
return res;
}
signed main() {
int n,m;
cin >> n >> m;
int sum = 1;
for (int i = 1; i <= n; i++) {
int t;
cin >> t;
m-=t;
sum *= i;
}
int ans = 0;
for (int i = 0; i <= m; i++) {
ans += c(i+n-1,n-1);
ans %= mod;
}cout << ans << endl;
return 0;
}
D - 简单的素数
题解:
判断素数。
代码:
#include
using namespace std;
#define int long long
int t;
signed main() {
cin >> t;
while(t--) {
int n;
cin >> n;
bool st = true;
for (int j = 2; j*j <= n; j++) {
if(n % j == 0) {
st = false;
break;
}
}
if(n == 1 || n == 2) st = true;
if(st)cout << "Yes" << endl;
else cout << "No" << endl;
}
return 0;
}
E - AND
题解:
质数是一定要判断的,可以利用欧拉筛线性判断素数,对于给出区间内,判断其中素数的个数,以及这个区间内有多少个子区间与操作后为0。
可以发现素数中只有2是偶数,最后一位二进制是0,所以只有它和别人与操作后有机会变成0,而2只要和从5开始的数字与都会是0,因此最后输出个数-2即可。
代码:
#include
using namespace std;
#define int long long
bool pri[100000005];
vectora;
int t;
signed main() {
cin >> t;
int sum = 0;
pri[1] = 1;
for (int i = 2; i <= 100000003; i++) {
if(!pri[i])a.push_back(i);
for (auto x : a) {
if(x*i > 100000003)break;
pri[x*i] = 1;
if(i % x == 0)break;
}
}
// cout << pri[1] << ' ' << pri[2] << ' ' << pri[3] << ' ' << pri[4] << ' ' << pri[9];
while(t--) {
int x,y;
cin >> x >> y;
int l = lower_bound(a.begin(),a.end(),x)-a.begin();
int r = upper_bound(a.begin(),a.end(),y)-a.begin();
cout << r-l << ' ';
if(x > 2) cout << 0 << endl;
else {
if(r-l == 1) cout << 0 << endl;
else cout << r-l-2 << endl;
}
}
return 0;
}
F - 小雷的算式
**
题解:
代码:
#include
using namespace std;
#define int long long
const int N = 2e5+5;
int a[N];
signed main() {
string s;
getline(cin,s);
int t = 0;
int res = 0;
for (int i = 0; i < s.length(); i++) {
if(s[i] == '+') {
a[t++] = res;
res = 0;
}
else res = res*10+(s[i]-'0');
}a[t] = res;
sort(a,a+t+1);
int sum = 0;
for (int i = t; i >= 1; i--) {
cout << a[i] << '+';
sum += a[i];
}
cout << a[0] << endl;
sum += a[0];
cout << sum << endl;
return 0;
}
H - 聪明且狡猾的恶魔
垃圾题目数据出错卡我一小时。
题解:
想象一下只剩下俩只恶魔的时候,所有的金币都会归为前面那只恶魔的,所以当有三只恶魔的时候,他就会给最后那只恶魔一枚金币,希望它能帮助自己,最后的恶魔当然会答应。所以每次只需要给最后不到一半的恶魔各一枚金币即可。
代码:
#include
using namespace std;
#define int long long
int t;
signed main() {
cin >> t;
while(t--) {
int x,n;
cin >> x >> n;
n = (n-1)/2;
cout << x-n << endl;
}
return 0;
}
I - 马拉松
I hate 图论
题解:
有n个城市,现在在任意俩个城市之间跑最短路,如果经过x城市跑到y城市会被禁止,问有多少次会被禁止。从每个城市出发可以到达城市中的其他城镇。也就是说,给定的城镇和道路地图是一棵树。
把x作为树根,从y的子节点包括它自己跑到x及x的别的子树,都是被禁止的,遍历一下每个节点的子节点有多少个,并把y的那颗树标记一下,等会减去它就是x的别的子树。
给出俩种相同思想的不同写法。
代码:
#include
using namespace std;
#define int long long
const int N = 3000005;
int n,x,y;
vectorl[3000005];
bool st[N];
int c[N];
void dfs(int x,int fa) {
c[x] = 1;
if(x == y) st[x] = true;
for (auto rs: l[x]) {
if(rs == fa)continue;
dfs(rs,x);
c[x] += c[rs];
if(st[rs])st[x] = true;
}
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
memset(st,0,sizeof st);
memset(c,0,sizeof c);
cin >> n >> x >> y;
for (int i = 1; i < n; i++) {
int a,b;
cin >> a >> b;
l[a].push_back(b);
l[b].push_back(a);
}
dfs(x,0);
int ans = 0;
for (auto cg : l[x]) {
if(st[cg]) ans += c[cg];
}
cout << c[y]*(c[x]-ans) << endl;
return 0;
}
#includeJ - 尖塔第四强的高手
思路其实不难,基本就是一道LCA变形题,但我当时真的不太会LCA,当然现在也不是很会谢谢。题意太复杂了上图。
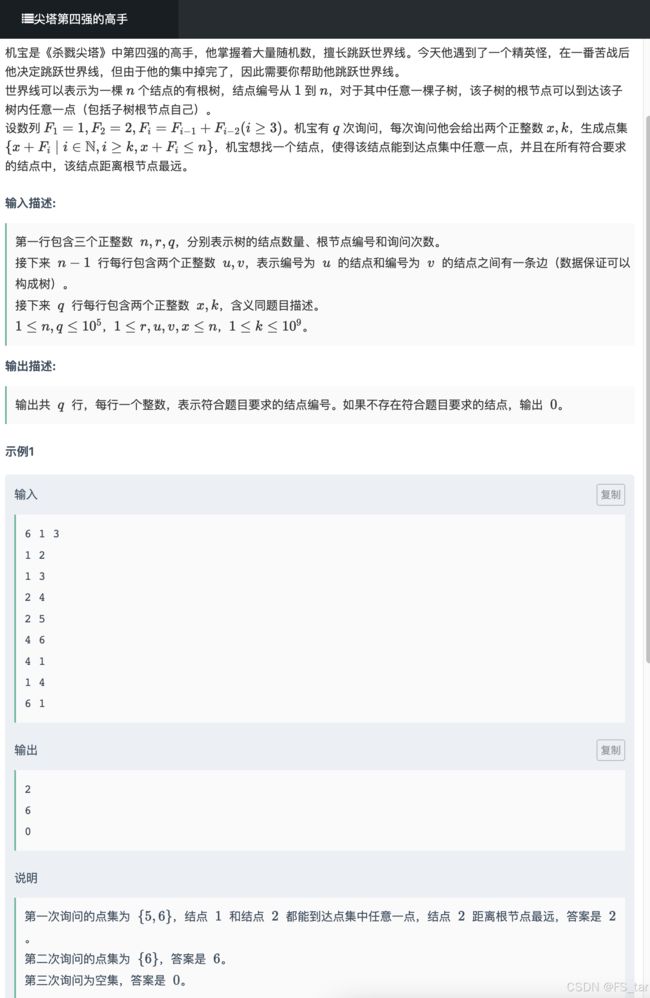
题解:
开始解读,可以发现k的范围非常大到1e9,但是斐波那契数列的增长其实非常快,所以只要k>25,其实就已经超过了n的范围,直接输出0即可。这个点比较关键,脑子要转一下。
LCA倍增算法的复杂度其实比较高,但是这道题给出的q组询问,每个区间的数的最近共同祖先,一个一个分别推导即可,不用n*n的复杂度,所以最大也就到24n,不会超时。
代码:
#include