机器学习基石笔记8——为什么机器可以学习（4）
转载请注明出处：http://www.cnblogs.com/ymingjingr/p/4271742.html
目录
机器学习基石笔记1——在何时可以使用机器学习(1)
机器学习基石笔记2——在何时可以使用机器学习(2)
机器学习基石笔记3——在何时可以使用机器学习(3)(修改版)
机器学习基石笔记4——在何时可以使用机器学习（4）
机器学习基石笔记5——为什么机器可以学习（1）
机器学习基石笔记6——为什么机器可以学习（2）
机器学习基石笔记7——为什么机器可以学习（3）
机器学习基石笔记8——为什么机器可以学习（4）
机器学习基石笔记9——机器可以怎样学习（1）
机器学习基石笔记10——机器可以怎样学习（2）
机器学习基石笔记11——机器可以怎样学习（3）
机器学习基石笔记12——机器可以怎样学习（4）
机器学习基石笔记13——机器可以怎样学得更好（1）
机器学习基石笔记14——机器可以怎样学得更好（2）
机器学习基石笔记15——机器可以怎样学得更好（3）
机器学习基石笔记16——机器可以怎样学得更好（4）
八、Noise and Error
噪音（杂讯）和错误。
8.1 Noise and Probabilistic Target
噪音（杂讯）和概率目标函数。
这一小节主要讨论有噪音（在2.4节提到的）的情况下是否VC限制仍可用，其流程图如图8-1所示。
图8-1 含有噪音的机器学习流程图
什么是噪音，或者噪音产生的原因有哪些？仍然举银行发放信用卡的例子，用来更形象的阐述产生噪音的3种原因：
-
标记y中存在的噪音，即错误的标记。如将本应该发放信用卡的用户，错误的标记为不符合规定的用户。
-
标记y中存在的另一种噪音，即不同的评判标准评定同一输入样本得到不同结果，如两个用户所有的属性条件都一致，标示为一个可以发放，而另一个不可以发放。
-
输入样本x中存在的噪音，即输入信息不准确，如用户的信息录入错误。
回到此节的重点，存在噪音时，VC限制还能起作用吗？接下来给予一个简单的推导，不同于前几章，此种情况的VC限制完整的重新推导一遍，本节主要提供的是一种证明思路。
小球罐子的例子再次登场，之前谈论的没有噪音条件时输入样本和整体样本都服从同一个概率分布
。不论是罐子中存在的小球还是抽样出来的小球，其颜色都是固定不变的。此种情况，使用的是确定性（deterministic）的小球。其中小球的颜色类比于目标函数f(x)与假设函数h(x)是否一致。标记y取决于目标函数f，此学习方法叫做判别方法；但是在现实中多数为含有噪音的情况，数据依然服从统一的概率分布，但小球颜色并不固定，可以想象为颜色在不停变色的小球，只能在某一时刻才能确定它的颜色，这种小球可以叫做概率性（probabilistic）的小球。对应到机器学习上，是含有噪音的样本，即
并不确定，其中标记y服从概率分布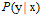
，这一形式被称为目标分布（target distribution）而不是目标函数，此方法叫做生成方法。
为何称为目标分布，举一个简单的例子，如一个样本点符合以下公式8-1。
（公式8-1）
则一定会选择错误率小的目标（mini-target），根据此原则该例选择标记为+1的，而中30%几率标记为-1又是什么意思呢？是噪音。目标函数f是一个特殊的目标分布，其概率符合公式8-2。
（公式8-2）
至此出现了两个分布函数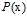
和
，
越大意味着x被选为训练样本的概率越大，
越大意味着该样本是某一类的几率越大，两者结合，即在常见的样本点上分的类尽量正确。
因此得出VC限制依然适用，因为这种含有噪音的输入样本以及标记分别服从
和
，即
服从
的联合概率分布。
了解了本节内容之后，结合噪音和目标分布的概念对机器学习流程图进行修改，如图8-2所示，其中目标函数f变成了目标分布
，它产生训练样本的标记y，同时测试的标记y也服从该分布。
图8-2 结合噪音与目标分布的机器学习流程图
8.2 Error Measure
错误衡量。
这一小节主要介绍错误的衡量方式对机器学习的影响。
以上很多章节都在描述如何使机器学到东西，即如何使得假设函数g和目标函数f接近，即如何使得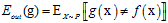 
尽可能的小。已知的错误衡量
都考虑了哪些问题呢？主要有以下三个因素：
-
整个样本空间（out-of-sample）：所有未知的样本x的平均；
-
一个点一个点评估(pointwise)：每个点单独评估；
-
使用分类（classification）的评估方式：
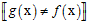，因为是二元分类只有两个类别，因此相同为0，不同为1。
上述这种分类的错误（classification error）又被叫做0/1错误（0/1 error）
可以使用函数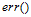
表示逐点的错误衡量（pointwise error measure），因此训练样本的错误衡量及整个样本空间的错误衡量可分别使用公式8-3和公式8-4表示。
（公式8-3）
（公式8-4）
为了表述的简单，又将假设函数
表示为
，目标函数
表示为
。
除了常用在分类（classification）上的0/1错误衡量之外，还有用在回归（regression）上的平方错误（square error）衡量，它也是一种逐点（pointwise）的错误衡量方式，如公式8-5所示。
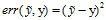（公式8-5）
给出了两种错误衡量的表达形式，接着讲一下错误衡量和学习之间的关系。错误衡量对机器学习有着指导作用。
在含有噪音的情况下，目标分布函数
和逐点错误函数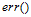
共同决定了理想的错误率最小目标函数（ideal mini-target）f。
目标分布函数
对错误率最小目标函数f的影响在上一节中已经阐述过了，接下来通过一个例子来说明逐点错误函数
对其的影响。
假设3个目标分布函数
，
，
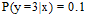。在0/1错误衡量的情况下，不难得出各类错误率，如图8-3所示。
图8-3 0/1错误衡量的情况下各标记的错误率
不难得出y=2时错误率最低，因此应选择y=2的标记，其中有个怪异的标记为1.9，该标记在0/1错误衡量的标准下错误率为1。
换一种错误衡量方式还是对这些目标分布的错误率进行计算，如图8-4为平方错误衡量下各标记的错误率。
图8-4 平方错误衡量下各标记的错误率
此时错误率最低的标记恰恰是在0/1错误衡量中错误率为1的标记1.9，因此使用平方错误衡量时选择标记y=1.9。
很容易推出在两种错误衡量下最小目标函数f可以分别使用公式8-6和公式8-7表示。
（公式8-6）
（公式8-7）
至此在上一节的基础上对机器学习流图做了进一步的修改，如图8-5所示，加入了错误衡量的模块，该模块对算法和最终的假设选择都起着很大影响。
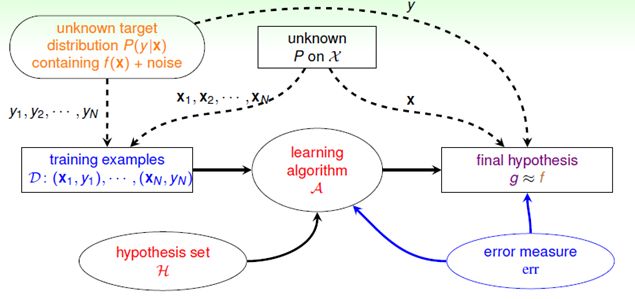
图8-5 含有错误衡量的机器学习流图
8.3 Algorithmic Error Measure
算法的错误衡量。
对于二元分类问题错误的类型也分为两类，如图8-6所示。
图8-6 分类错误的两种错误类型
在目标函数f为+1时，假设函数g却给出了-1，这种错误叫做错误的拒绝（false reject），另一种是在目标函数f为-1时，假设函数g却给出了+1，这种错误叫做错误的接受（false accept）。
上一节中提到的0/1错误衡量简单的将这两类错误的损失画上了等号，其实在现实中这两种错误在不同的场景其损失是不同的。
举两个常见的例子，在超市给年消费额高的会员发放赠品时，如果出现了错误的接受，就意味着该会员没有资格领取到赠品，超市还是给他发放了赠品，该损失只是超市多发了一些赠品；但如果是错误的拒绝，意味着该会员有资格领取到赠品，超市却拒绝给他发放了，这损失的是超市的信誉，可能就会因此大批的用户。另一个例子是在安全部门中，员工有查看某一资料的权限，系统却拒绝了他的请求，这是一种错误的拒绝，作为员工，最多也就是抱怨一下，但是如果是一个员工没有查看某一资料的权限，系统却同意了，这是一种错误的接受，这个损失就可能会非常大，甚至有可能威胁到国家的利益。这两种情况的损失可能如图8-7所示。
图8-7 a)超市发放赠品的错误损失 b）安全部门的错误损失
这两个错误损失也证明了在不同的应用中需要使用不同的错误衡量。
在设计算法时，最好方式当然按照各种错误损失的情况设计错误衡量，用到算法中去，但是最大的问题是错误损失的数值如何确定（如图中这些10和1000如何定量的给出）。因此在进行算法设计时，通常采用替代的方式来进行设计，目前主要有两种替代方式的原则，如下所示：
-
可以说得通：在分类错误衡量中，可以想象这种噪音的情况相对于整体一定是小的，因此只需要找到一个足够小的错误即可；在平方错误衡量中，只要认同噪音服从高斯分布，减小高斯中平方项，就如同在减少平方错误。将这种近似的错误衡量方式用
表示。
-
友善的：很容易设计一种算法A。如寻找最小的0/1错误是一个NP难问题，而真正在做的算法时，运用错误率比前者更小的原则，即寻找越来越小的错误率。以后的章节中会提到两种方式：直接求出结果（closed-form solution）；凸求解方程（convex objective function）。
因为在设计算法时，很难知道具体的错误衡量，因此产生了近似的错误衡量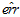
，这是本节的重点，在加入了
之后，机器学习的流程图如图8-8所示。
图8-8使用近似错误衡量
的机器学习流图
8.4 Weighted Classification
加权分类。
上一节中提到的如图8-3存在的这种错误表示方式，可以称之为成本矩阵（cost matrix）或损失矩阵（loss matrix）再或者错误矩阵（error matrix）。
图8-3 错误矩阵
使用如上的错误矩阵分别表示
与
，如公式8-8和公式8-9所示。
（公式8-8）
（公式8-9）
因为VC限制可以在各种算法中起作用，因此在求解已知的算法中只需要使得
尽可能的小，但是这里使用的
和之前的提到的没有加权的
还是有些区别，为了有所区分，将加权的（weighted）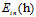
表示为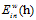
，公式如8-10所示。
（公式8-10）
假设在一种不是线性可分的情况下（如果是线性可分一定会产生
的情况），比如pocked算法，先对在这一情况时算法思路进行一个猜想，大部分和原来的算法一致，即如果
的
比
的更小，则使用
取代原来的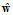
。
Pocket算法可以使用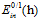
作为错误衡量是被证明了的，但是上述加权的方式却没有被证明，该如何寻找一种保障pocket算法在加权错误的情况下，可以使用类似以上的方式的算法流程呢？
一个简单的方式是将上述使用
的原始问题转变成一种使用
且与原始问题等价的问题，如图8-4所示。
图8-4 a)使用
的原始问题 b) 使用 
的等价问题
等价问题是将原始问题中数据集D中标记为-1的所有数据样本都复制1000次，再将损失矩阵表示不含加权的损失矩阵，而这种损失矩阵正是pocket算法使用的错误衡量方式，唯一的区别，如样本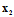
出错，被复制的其他的999个
也跟着一起犯错了，损失相当于是以前的1000倍。当然细心的人已经发现了，在算法做搜寻的过程中碰到标记为-1的数据样本的几率也增大了1000。