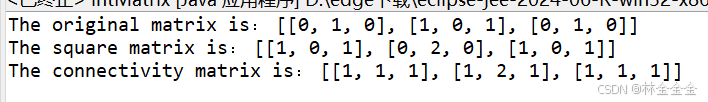日撸Java三百行(day31:整数矩阵及其运算)
目录
前言
一、基本属性与方法
二、getter与setter方法
三、矩阵相加与矩阵相乘方法
1.矩阵相加
2.矩阵相乘
四、数据测试
五、完整的程序代码
总结
前言
从今天开始,我们就要踏上图论的学习之路了。第一天,我们先简单热个身,构造一个整数矩阵。
一、基本属性与方法
/**
* The data.
*/
int[][] data;由于我们今天构造的是int类型的矩阵,而在程序代码中矩阵又是通过数组来实现,所以这里首先定义了一个int类型的二维数组。
/**
*********************
* The first constructor.
*
* @param paraRows The number of rows.
* @param paraColumns The number of columns.
*********************
*/
public IntMatrix(int paraRows, int paraColumns) {
data = new int[paraRows][paraColumns];
} // Of the first constructor创建第一个构造方法,这其实就是我在日撸Java三百行(day07:矩阵元素相加)中所提到过的二维数组的动态初始化,paraRows代表该数组的行数,paraColumns代表该数组的列数。
/**
*********************
* The second constructor. Construct a copy of the given matrix.
*
* @param paraMatrix The given matrix.
*********************
*/
public IntMatrix(int[][] paraMatrix) {
data = new int[paraMatrix.length][paraMatrix[0].length];
// Copy elements.
for (int i = 0; i < data.length; i++) {
for (int j = 0; j < data[0].length; j++) {
data[i][j] = paraMatrix[i][j];
} // Of for j
} // Of for i
} // Of the second constructor创建第二个构造方法,简单来说就是输入一个二维数组作为参数,再将其拷贝到我们所构造的数组。与日撸Java三百行(day07:矩阵元素相加)中矩阵所有元素求和的分析保持一致,这里的paraMatrix.length仍然代表数组paraMatrix的行数,paraMatrix[0].length则代表数组paraMatrix的列数;然后利用一个两层for循环,将参数数组paraMatrix中的元素一个一个拷贝到目标数组data中。
/**
*********************
* The third constructor. Construct a copy of the given matrix.
*
* @param paraMatrix The given matrix.
*********************
*/
public IntMatrix(IntMatrix paraMatrix) {
this(paraMatrix.getData());
} // Of the third constructor创建第三个构造方法,与第二个构造方法不同的是,这里的参数不再是二维数组,而是同为IntMatrix类型的一个对象;然后,再利用this调用其他构造方法以减少代码冗余,调用的构造方法为getData(),具体的我们后面再说。本质上看,第三个构造方法其实与第二个构造差不多,都是通过拷贝输入的参数(数组或矩阵)进行构造。
/**
*********************
* Get identity matrix. The values at the diagonal are all 1.
*
* @param paraRows The given rows.
*********************
*/
public static IntMatrix getIdentityMatrix(int paraRows) {
IntMatrix resultMatrix = new IntMatrix(paraRows, paraRows);
for (int i = 0; i < paraRows; i++) {
// According to access control, resultMatrix.data can be visited
// directly.
resultMatrix.data[i][i] = 1;
} // Of for i
return resultMatrix;
} // Of getIdentityMatrix此外,我们还创建了一个单位矩阵的方法。根据线性代数的知识可知,单位矩阵的行数=列数,且主对角线上全为1,因此我们定义一个IntMatrix类的对象resultMatrix;然后将resultMatrix的data属性初始化,使得其主对角线上全为1;最后再返回resultMatrix。
/**
*********************
* Overrides the method claimed in Object, the superclass of any class.
*********************
*/
public String toString() {
return Arrays.deepToString(data);
} // Of toString这里我们同样利用toString()方法进行遍历,在日撸Java三百行(day07:矩阵元素相加)中,我们就说过,Arrays.deepToString(数组名)用于输出多维数组的字符串形式。
二、getter与setter方法
getter方法和setter方法是面向对象编程中非常常用的方法,主要是用于访问和修改对象的属性(成员变量),具体如下:
- Getter方法,也叫访问器,用于访问对象的属性值,它不接受任何参数,但要返回属性的值。Getter方法的命名常以“get”开头,后接属性的名称。
- Setter方法,也叫修改器,用于修改对象的属性值,它接受参数,并用参数的值来更新属性的值。Setter方法的命名常以“set”开头,后接属性的名称。
总之,通过getter方法其他类可以获取属性的值而不用直接访问属性,通过setter方法其他类可以修改属性的值而不用直接修改属性,二者有效控制了对对象属性的访问和修改,相当于进行了封装,提高了安全性。
今天具体用到的getter方法与setter方法如下:
/**
*********************
* Get my data. Warning, the reference to the data instead of a copy of the
* data is returned.
*
* @return The data matrix.
*********************
*/
public int[][] getData() {
return data;
} // Of getData
/**
*********************
* Getter.
*
* @return The number of rows.
*********************
*/
public int getRows() {
return data.length;
} // Of getRows
/**
*********************
* Getter.
*
* @return The number of columns.
*********************
*/
public int getColumns() {
return data[0].length;
} // Of getColumns
/**
*********************
* Set one the value of one element.
*
* @param paraRow The row of the element.
* @param paraColumn The column of the element.
* @param paraValue The new value.
*********************
*/
public void setValue(int paraRow, int paraColumn, int paraValue) {
data[paraRow][paraColumn] = paraValue;
} // Of setValue
/**
*********************
* Get the value of one element.
*
* @param paraRow The row of the element.
* @param paraColumn The column of the element.
*********************
*/
public int getValue(int paraRow, int paraColumn) {
return data[paraRow][paraColumn];
} // Of getValue- getData(): 用于获取对象的data属性值
- getRows():用于获取对象的行数属性值
- getColumns():用于获取对象的列数属性值
- setValue():用于修改对象data属性的某个元素值
- getValue():用于获取对象data属性的某个元素值
三、矩阵相加与矩阵相乘方法
1.矩阵相加
/**
*********************
* Add another matrix to me.
*
* @param paraMatrix The other matrix.
*********************
*/
public void add(IntMatrix paraMatrix) throws Exception {
// Step 1. Get the data of the given matrix.
int[][] tempData = paraMatrix.getData();
// Step 2. Size check.
if (data.length != tempData.length) {
throw new Exception("Cannot add matrices. Rows not match: " + data.length + " vs. "
+ tempData.length + ".");
} // Of if
if (data[0].length != tempData[0].length) {
throw new Exception("Cannot add matrices. Rows not match: " + data[0].length + " vs. "
+ tempData[0].length + ".");
} // Of if
// Step 3. Add to me.
for (int i = 0; i < data.length; i++) {
for (int j = 0; j < data[0].length; j++) {
data[i][j] += tempData[i][j];
} // Of for j
} // Of for i
} // Of add这里我们创建了一个外部输入矩阵与当前矩阵的加法运算,由于只有同型矩阵(即行数和列数均相等的矩阵)才能相加,所以在执行加法之前我们通过两个if语句来判断是否为同型矩阵;确定为同型矩阵后,再利用两层for循环实现相加。
接着,在此基础上我们又创建了一个方法,用于实现外部输入两个矩阵的相加,具体来说就是将其中一个外部输入矩阵作为当前矩阵,然后调用“外部输入矩阵与当前矩阵的加法运算”,代码如下:
/**
*********************
* Add two existing matrices.
*
* @param paraMatrix1 The first matrix.
* @param paraMatrix2 The second matrix.
* @return A new matrix.
*********************
*/
public static IntMatrix add(IntMatrix paraMatrix1, IntMatrix paraMatrix2) throws Exception {
// Step 1. Clone the first matrix.
IntMatrix resultMatrix = new IntMatrix(paraMatrix1);
// Step 2. Add the second one.
resultMatrix.add(paraMatrix2);
return resultMatrix;
} // Of add2.矩阵相乘
/**
*********************
* Multiply two existing matrices.
*
* @param paraMatrix1 The first matrix.
* @param paraMatrix2 The second matrix.
* @return A new matrix.
*********************
*/
public static IntMatrix multiply(IntMatrix paraMatrix1, IntMatrix paraMatrix2)
throws Exception {
// Step 1. Check size.
int[][] tempData1 = paraMatrix1.getData();
int[][] tempData2 = paraMatrix2.getData();
if (tempData1[0].length != tempData2.length) {
throw new Exception("Cannot multiply matrices: " + tempData1[0].length + " vs. "
+ tempData2.length + ".");
} // Of if
// Step 2. Allocate space.
int[][] resultData = new int[tempData1.length][tempData2[0].length];
// Step 3. Multiply.
for (int i = 0; i < tempData1.length; i++) {
for (int j = 0; j < tempData2[0].length; j++) {
for (int k = 0; k < tempData1[0].length; k++) {
resultData[i][j] += tempData1[i][k] * tempData2[k][j];
} // Of for k
} // Of for j
} // Of for i
// Step 4. Construct the matrix object.
IntMatrix resultMatrix = new IntMatrix(resultData);
return resultMatrix;
} // Of multiply
在日撸Java三百行(day08:矩阵相乘) 中,我们就已经详细地介绍过矩阵相乘的相关内容了,所以这里就不再重复赘述了。
四、数据测试
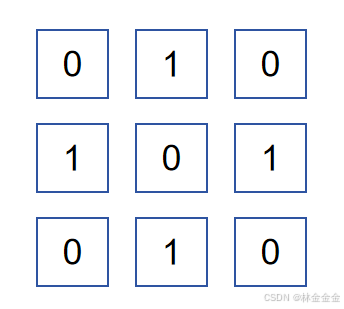
接着,我们创建如下的矩阵用于数据测试:
由于我们创建tempMatrix1对象时只规定了它的行数和列数,而int类型的默认初始值为0,所以矩阵tempMatrix1的元素刚开始全为0,然后我们通过setValue()方法对某些元素值进行了修改,最后就得到了如上图的矩阵。
/**
*********************
* The entrance of the program.
*
* @param args Not used now.
*********************
*/
public static void main(String args[]) {
IntMatrix tempMatrix1 = new IntMatrix(3, 3);
tempMatrix1.setValue(0, 1, 1);
tempMatrix1.setValue(1, 0, 1);
tempMatrix1.setValue(1, 2, 1);
tempMatrix1.setValue(2, 1, 1);
System.out.println("The original matrix is: " + tempMatrix1);
IntMatrix tempMatrix2 = null;
try {
tempMatrix2 = IntMatrix.multiply(tempMatrix1, tempMatrix1);
} catch (Exception ee) {
System.out.println(ee);
} // Of try
System.out.println("The square matrix is: " + tempMatrix2);
IntMatrix tempMatrix3 = new IntMatrix(tempMatrix2);
try {
tempMatrix3.add(tempMatrix1);
} catch (Exception ee) {
System.out.println(ee);
} // Of try
System.out.println("The connectivity matrix is: " + tempMatrix3);
} // Of main五、完整的程序代码
package matrix;
import java.util.Arrays;
/**
* Int matrix. For efficiency we do not define ObjectMatrix. One can revise it
* to obtain DoubleMatrix.
*
*@auther Xin Lin [email protected].
*/
public class IntMatrix {
/**
* The data.
*/
int[][] data;
/**
*********************
* The first constructor.
*
* @param paraRows The number of rows.
* @param paraColumns The number of columns.
*********************
*/
public IntMatrix(int paraRows, int paraColumns) {
data = new int[paraRows][paraColumns];
} // Of the first constructor
/**
*********************
* The second constructor. Construct a copy of the given matrix.
*
* @param paraMatrix The given matrix.
*********************
*/
public IntMatrix(int[][] paraMatrix) {
data = new int[paraMatrix.length][paraMatrix[0].length];
// Copy elements.
for (int i = 0; i < data.length; i++) {
for (int j = 0; j < data[0].length; j++) {
data[i][j] = paraMatrix[i][j];
} // Of for j
} // Of for i
} // Of the second constructor
/**
*********************
* The third constructor. Construct a copy of the given matrix.
*
* @param paraMatrix The given matrix.
*********************
*/
public IntMatrix(IntMatrix paraMatrix) {
this(paraMatrix.getData());
} // Of the third constructor
/**
*********************
* Get identity matrix. The values at the diagonal are all 1.
*
* @param paraRows The given rows.
*********************
*/
public static IntMatrix getIdentityMatrix(int paraRows) {
IntMatrix resultMatrix = new IntMatrix(paraRows, paraRows);
for (int i = 0; i < paraRows; i++) {
// According to access control, resultMatrix.data can be visited
// directly.
resultMatrix.data[i][i] = 1;
} // Of for i
return resultMatrix;
} // Of getIdentityMatrix
/**
*********************
* Overrides the method claimed in Object, the superclass of any class.
*********************
*/
public String toString() {
return Arrays.deepToString(data);
} // Of toString
/**
*********************
* Get my data. Warning, the reference to the data instead of a copy of the
* data is returned.
*
* @return The data matrix.
*********************
*/
public int[][] getData() {
return data;
} // Of getData
/**
*********************
* Getter.
*
* @return The number of rows.
*********************
*/
public int getRows() {
return data.length;
} // Of getRows
/**
*********************
* Getter.
*
* @return The number of columns.
*********************
*/
public int getColumns() {
return data[0].length;
} // Of getColumns
/**
*********************
* Set one the value of one element.
*
* @param paraRow The row of the element.
* @param paraColumn The column of the element.
* @param paraValue The new value.
*********************
*/
public void setValue(int paraRow, int paraColumn, int paraValue) {
data[paraRow][paraColumn] = paraValue;
} // Of setValue
/**
*********************
* Get the value of one element.
*
* @param paraRow The row of the element.
* @param paraColumn The column of the element.
*********************
*/
public int getValue(int paraRow, int paraColumn) {
return data[paraRow][paraColumn];
} // Of getValue
/**
*********************
* Add another matrix to me.
*
* @param paraMatrix The other matrix.
*********************
*/
public void add(IntMatrix paraMatrix) throws Exception {
// Step 1. Get the data of the given matrix.
int[][] tempData = paraMatrix.getData();
// Step 2. Size check.
if (data.length != tempData.length) {
throw new Exception("Cannot add matrices. Rows not match: " + data.length + " vs. "
+ tempData.length + ".");
} // Of if
if (data[0].length != tempData[0].length) {
throw new Exception("Cannot add matrices. Rows not match: " + data[0].length + " vs. "
+ tempData[0].length + ".");
} // Of if
// Step 3. Add to me.
for (int i = 0; i < data.length; i++) {
for (int j = 0; j < data[0].length; j++) {
data[i][j] += tempData[i][j];
} // Of for j
} // Of for i
} // Of add
/**
*********************
* Add two existing matrices.
*
* @param paraMatrix1 The first matrix.
* @param paraMatrix2 The second matrix.
* @return A new matrix.
*********************
*/
public static IntMatrix add(IntMatrix paraMatrix1, IntMatrix paraMatrix2) throws Exception {
// Step 1. Clone the first matrix.
IntMatrix resultMatrix = new IntMatrix(paraMatrix1);
// Step 2. Add the second one.
resultMatrix.add(paraMatrix2);
return resultMatrix;
} // Of add
/**
*********************
* Multiply two existing matrices.
*
* @param paraMatrix1 The first matrix.
* @param paraMatrix2 The second matrix.
* @return A new matrix.
*********************
*/
public static IntMatrix multiply(IntMatrix paraMatrix1, IntMatrix paraMatrix2)
throws Exception {
// Step 1. Check size.
int[][] tempData1 = paraMatrix1.getData();
int[][] tempData2 = paraMatrix2.getData();
if (tempData1[0].length != tempData2.length) {
throw new Exception("Cannot multiply matrices: " + tempData1[0].length + " vs. "
+ tempData2.length + ".");
} // Of if
// Step 2. Allocate space.
int[][] resultData = new int[tempData1.length][tempData2[0].length];
// Step 3. Multiply.
for (int i = 0; i < tempData1.length; i++) {
for (int j = 0; j < tempData2[0].length; j++) {
for (int k = 0; k < tempData1[0].length; k++) {
resultData[i][j] += tempData1[i][k] * tempData2[k][j];
} // Of for k
} // Of for j
} // Of for i
// Step 4. Construct the matrix object.
IntMatrix resultMatrix = new IntMatrix(resultData);
return resultMatrix;
} // Of multiply
/**
*********************
* The entrance of the program.
*
* @param args Not used now.
*********************
*/
public static void main(String args[]) {
IntMatrix tempMatrix1 = new IntMatrix(3, 3);
tempMatrix1.setValue(0, 1, 1);
tempMatrix1.setValue(1, 0, 1);
tempMatrix1.setValue(1, 2, 1);
tempMatrix1.setValue(2, 1, 1);
System.out.println("The original matrix is: " + tempMatrix1);
IntMatrix tempMatrix2 = null;
try {
tempMatrix2 = IntMatrix.multiply(tempMatrix1, tempMatrix1);
} catch (Exception ee) {
System.out.println(ee);
} // Of try
System.out.println("The square matrix is: " + tempMatrix2);
IntMatrix tempMatrix3 = new IntMatrix(tempMatrix2);
try {
tempMatrix3.add(tempMatrix1);
} catch (Exception ee) {
System.out.println(ee);
} // Of try
System.out.println("The connectivity matrix is: " + tempMatrix3);
} // Of main
} // Of class IntMatrix运行结果
总结
总的来说,今天的内容以及代码难度还是比较简单的,毕竟我们之前已经学过矩阵的一些运算了,所以今天的整数矩阵可以算是一个回顾;不过同时,今天也是一个铺垫,因为明天我们就会学习图的连通性,会涉及到邻接矩阵、连通矩阵,这就需要以今天的内容为基础进行延伸。