UVa 11524:In-Circle（解析几何）

Problem E
In-Circle
Input: Standard Input

Output: Standard Output

 

In-circle of a triangle is the circle that touches all the three sides of the triangle internally. The center of the in-circle of a triangle happens to be the common intersection point of the three bisectors of the internal angles. In this problem you will not be asked to find the in-circle of a triangle, but will be asked to do the opposite!!

 
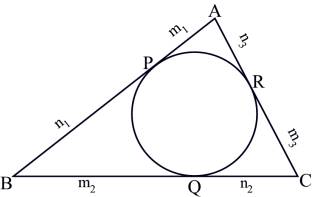
You can see in the figure above that the in-circle of triangle ABC touches the sides AB, BC and CA at point P, Q and R respectively and P, Q and R divides AB, BC and CA in ratio m1:n1, m2:n2 and m3:n3 respectively. Given these ratios and the value of the radius of in-circle, you have to find the area of triangle ABC.

 

Input

First line of the input file contains an integer N (0<N<50001), which denotes how many input sets are to follow. The description of each set is given below.

 

Each set consists of four lines. The first line contains a floating-point number r (1<r<5000), which denotes the radius of the in-circle. Each of the next three lines contains two floating-point numbers, which denote the values of m₁, n₁, m₂, n₂, m₃ and n₃ (1<m₁, n₁, m₂, n₂, m₃, n₃<50000) respectively.

                                                           

Output

For each set of input produce one line of output. This line contains a floating-point number that denotes the area of the triangle ABC. This floating-point number should contain four digits after the decimal point. Errors less than 5*10^-3 will be ignored. Use double-precision floating-point number for calculation.

 

Sample Input                               Output for Sample Input

2 140.9500536497 15.3010457320 550.3704847907 464.9681681852 65.9737378230 55.0132446384 10.7791711946 208.2835101182 145.7725891419 8.8264176452 7.6610997600 436.1911036207 483.6031801012 140.2797089713

400156.4075 908824.1322

---

Problemsetter: Shahriar Manzoor

Special Thanks: Mohammad Mahmudur Rahman

---

 

　　解析几何。

　　思路是先设AP=AC=x，则根据比例关系可以知道：

　　三边　　a = (n1+m1)/m1*x;　　b = (n3+m3)/n3*x;　　c = m3/n3*(n2+m2)/n2*x;

　　将系数提出，设 k1 = (n1+m1)/m1;　　k2 = (n3+m3)/n3;　　k3 = m3/n3*(n2+m2)/n2;

　　由海伦公式可知 S = sqrt(p*(p-a)*(p-b)*(p-c));　　（p = (a+b+c)/2）　　//公式一

　　由边和半径的也能求出三角形的面积 S = (a*r+b*r+c*r)/2 = p*r;　　　　　　//公式二

　　联立公式一和公式二可得：

　　x = 2*sqrt(r*r*(k1+k2+k3)/((k2+k3-k1)*(k1+k3-k2)*(k1+k2-k3)));

　　带入公式一得：

　　S = (k1+k2+k3)*x*r/2;

　　PS：代码很短，主要是分析过程。

　　代码：

 1 #include <iostream>

 2 #include <cmath>

 3 #include <iomanip>

 4 using namespace std;  5 int main()  6 {  7     int n;  8     cin>>n;  9     while(n--){ 10         double r; 11         double m1, n1, m2, n2, m3, n3; 12         cin>>r;    //输入半径

13         cin>>m1>>n1>>m2>>n2>>m3>>n3;    //输入比例

14         double k1,k2,k3; 15         k1 = (n1+m1)/m1; 16         k2 = m3*(n2+m2)/(n3*n2); 17         k3 = (n3+m3)/n3; 18         double x = 2*sqrt(r*r*(k1+k2+k3)/((k2+k3-k1)*(k1+k3-k2)*(k1+k2-k3)));    //设AP=AR=x

19         double s = (k1+k2+k3)*x*r/2; 20         cout<<setiosflags(ios::fixed)<<setprecision(4); 21         cout<<s<<endl; 22  } 23     return 0; 24 }

 

Freecode : www.cnblogs.com/yym2013