概率算法-n皇后的LV算法
概率算法结束了,要交作业了,其中一个题目是用LV算法解n皇后问题,并且给出当皇后数为12-20时,对于的随机放置皇后数(stepVegas)值。
不想全部从头写,打算找一个用回溯法求解n皇后的正确代码(因为lv算法里面有用到回溯部分),如果找到了,只需修改部分就可以用了。
问题是百度了一下,没找到靠谱的,最后在博客园里找了下,找到一位仁兄给的源码(http://www.cnblogs.com/djcsch2001/archive/2011/05/03/2035146.html#2234062),
虽然有个小错误,但是其它都对,算法写的很精炼。有了回溯法,修改就方便了。
回溯法是采用了穷举遍历的思想,优点是可以一次性找到所有解,缺点是算法性能较差。
由于n皇后的解是离散分布的,导致了在遍历搜索的过程中,很多都是做“无用功”。
这个时候LV算法就有了用武之地,先随机放置stepVegas个皇后(在前stepVegas行),剩下的n-stepVegas行调用回溯算法就行了。
由于遍历搜索的范围缩小,算法所需时间减少,响应的返回的解也只是部分解。但是可以通过多次执行返回更多的解。
这里还有一个问题就是stepVegas的值取多少最好,stepVegas过小,遍历搜索范围缩小不明显,算法时间过长,返回的解多。
stepVegas过大,遍历搜索范围小,但是随机放置stepVegas个满足要求的皇后同样需要花费大量时间。
事实上stepVegas的个数与n皇后解的分布情况有关。
举个例子,对于8后而言一共有92个解:
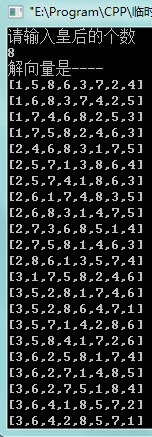
简要统计
第1行皇后放第1列的解有4个。
第1行皇后放第2列的解有8个。
.....
分析前两个皇后
第1行皇后放第1列,第2行皇后必须放5,6,7才有解。7解最多。
第1行皇后放第2列,第2行皇后必须放4,5,6,7,8才有解。
第1行皇后放第3列,第2行皇后必须放1,5,6,7,8才有解。6解最多。
.....
可以看到无论第一行皇后也即第一个皇后放哪,都有可行解。这个时候stepVegas=1显然不好,因为要返回所有解就必须随机取遍
所有位置。要返回所有解的话整体上的性能还不如回溯法。stepVegas=2,由于并不是每个随机组合都有解,此时可以体现LV算法的优势。
关于n皇后解的分布规律问题,本文不做进一步阐述,有兴趣的可以自己琢磨琢磨。
为了给出对与n皇后Lv算法中stepVegas的值取多少教好,决定以找到一个解的平均时间代价为评价指标。
下面是代码部分,里面有lv算法也有回溯法:
 LV算法和回溯法
LV算法和回溯法
1 #include <iostream>
2 #include<ctime>
3 using namespace std;
4
5 bool place(int x[],int k);//放置第k个皇后时,判断是否冲突。
6 void lv(int n,int x[],int stepVegas);//LV算法,先随机放置stepVegas个皇后
7 void queen(int n,int x[]);//普通回溯法
8 void output(int n,int x[]);//用于输出解向量,x[i]表示第i行的皇后放置的列
9
10 int main()
11 {
12 int stepVegas,n;
13 cout<<"请输入皇后的个数\n";//n皇后
14 cin>>n;
15 int *x=new int[n+1];//x[n]用于存放解向量
16 cout<<"解向量是----\n";
17 for (stepVegas=1;stepVegas<n/2;stepVegas++)
18 {
19 lv(n,x,stepVegas);
20 }
21 //queen(n,x);
22 delete [] x;
23 return 1;
24 }
25
26 bool place(int x[],int k)
27 {
28 for(int i=1;i<k;i++)
29 if((x[i]==x[k])||(abs(x[i]-x[k])==abs(i-k)))//不同列,且不在对角线上
30 return 0;
31 return 1;
32 }
33 void lv(int n,int x[],int stepVegas)
34 {
35 int k,temp;
36 int *y=new int[n+1];
37 long num=0;//num记录解数
38 float start,finish;//记录开始和结束时间
39 start = clock();//记录运行开始时间
40 srand( (unsigned)time( NULL ) );
41 for (k=1;k<n+1;k++)
42 {
43 y[k]=k;//把1-n放到数组y中
44 }
45 k=1;
46 while (k<=stepVegas)
47 {
48 temp=rand()%(n+1-k)+1;
49 x[k]=y[temp];//在可行数据域中随机选
50 if (place(x,k))
51 {
52 if (temp!=n+1-k)//取得不是最后一个数,需要对y进行整理,主要是避免用随机数产生了相同的数
53 {
54 y[temp]=y[n+1-k];//把最后一个数与第temp个交换
55 }
56 k++;
57 }
58 }
59 x[k]=0;
60 while(k>stepVegas)
61 {
62 x[k]+=1;//每个皇后都从第一列开始试,或者是回溯到上一个皇后尝试下一列
63 while((x[k]<=n)&&(!place(x,k)))//第k个皇后放置冲突
64 x[k]+=1;//尝试下一列
65 if(x[k]<=n)
66 if(k==n)//找到一个解
67 {
68 num++;
69 //output(n,x);
70 }
71 else
72 x[++k]=0;//开始第k+1个皇后
73 else//此时发现第k个皇后没有可行位置
74 x[k--]=0;//退回重试
75 }
76 finish = clock();//记录运行结束时间
77 cout<<"LV("<<stepVegas<<")法找到"<<num<<"个解\n";
78 cout<<"time:"<<(float)(finish - start) /1000<<endl;
79 cout<<"平均找一个解所花时间为:"<<(float)(finish - start) /1000/num<<endl<<endl;
80 delete [] y;
81 }
82 void queen(int n,int x[])
83 {
84 float start,finish;//记录开始和结束时间
85 start = clock();//记录运行开始时间
86 int k=1;//从第1个皇后开始放起
87 long num=0;//num记录解数
88 x[1]=0;
89 while(k>0)
90 {
91 x[k]+=1;//每个皇后都从第一列开始试,或者是回溯到上一个皇后尝试下一列
92 while((x[k]<=n)&&(!place(x,k)))//第k个皇后放置冲突
93 x[k]+=1;//尝试下一列
94 if(x[k]<=n)
95 if(k==n)//找到一个解
96 {
97 num++;
98 //output(n,x);
99 }
100 else
101 x[++k]=0;//开始第k+1个皇后
102 else//此时发现第k个皇后没有可行位置
103 x[k--]=0;//退回重试
104 }
105 finish = clock();//记录运行结束时间
106 cout<<"回溯法找到"<<num<<"个解\n";
107 cout<<"time:"<<(float)(finish - start) /1000<<endl;
108 cout<<"平均找一个解所花时间为:"<<(float)(finish - start) /1000/num<<endl;
109 }
110 void output(int n,int x[])
111 {
112 cout<<"[";
113 for(int i=1;i<n;i++)
114 cout<<x[i]<<",";
115 cout<<x[n]<<"]"<<endl;
116 return;
117 }
概率算法已经结束了,虽然很多算法在工程实践中应用不大比如:概率计数、素数判定等,有兴趣的可以看看。
但是概率算法的思想还是很有用的,特别是sherwood和las vegas。
sherwood使算法性能与实例无关,而依赖与概率。
las vegas使算法较快的找到部分解。
