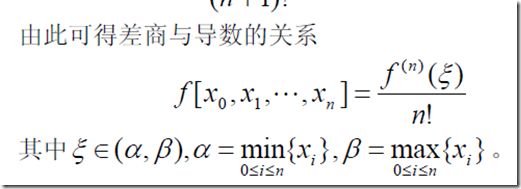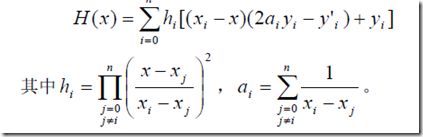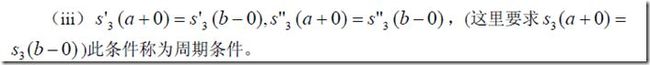建模算法(八)——插值
插值:求过已知有限个数据点的近似函数
拟合:已知有限个数据点,求近似函数,不要求过已知数据点,只要求在某种意义下在这些点的误差最小
(一)插值方法
一、拉格朗日多项式插值
1、插值多项式
就是做出一个多项式函数,经过给出的n个节点,并尽可能的接近原函数,将点带入多项式函数得到一个线性方程组
当系数矩阵满秩时,有唯一解。而,系数矩阵的行列式为
这是一个范德蒙德行列式,只要各个节点不同时,行列式就不为0,因此可得,一定能够解出系数方程
还有些指标
2、拉格朗日插值多项式
3、MATLAB实现
function y=lagrange(x0,y0,x)
%n个数据以数组x0,y0输入,m个插值点以数组x输入,输出数组y为m个插值。 n=length(x0);m=length(x); for i=m; z=x(i); s=0.0; for k=1:n p=1.0; for j=1:n; if j~=k p=p*(z-x0(j))/(x0(k)-x0(j)); end end s=p*y0(k)+s; end y(i)=s; end
二、牛顿插值
1、差商
2、牛顿插值公式
有点就是,多一个数据点,只多一项
PS:
3、差分
4、等距节点插值公式
三、分段线性插值
1、插值多项式的振荡
即如果插值多项式的次数越高,越容易发生振荡,不能很好的拟合。
2、分段线性插值
3、MATLAB实现
四、Hermite插值
1、Hermite插值多项式
2、MATLAB实现
function y-hermite(x0,y0,y1,x); %x0,y0为样本点数据,y1为导数指,m个插值点以数组x输入,输出数组y为m个插值 n=length(x0);m=length(x); for k=1:m; yy=0.0; for i=1:n h=1.0; a=0.0; for j=i:n if j~=i h=h*((x(k)-x0(j))/(x0(i)-x0(j)))^2; a=1/(x0(i)-x0(j))+a; end end yy=yy+h*((x0(i)-x0(k))*(2*a*y0(i)-y(i))+y0(i)); end y(k)=yy; end
五、样条插值
1、概念
实际中最常用的是k=2和k=3的情况
二、二次样条函数插值
二次样条函数有n+2个待定常数,所以要有n+2个条件,才能有唯一解
一定要有一个条件为一阶导数
三、三次样本函数插值
二次样条函数有n+3个待定常数,所以要有n+3个条件,才能有唯一解
四、三次插值在MATLAB中的实现
部分转载
1、y=interp1(x0,y0,x,`spline`); % (spline改成linear,则变成线性插值)
2、y=spline(x0,y0,xi);%这个是根据己知的x,y数据,用样条函数插值出xi处的值。即由x,y的值计算出xi对应的函数值。
3、pp=spline(x0,y0);%是由根据己知的x,y数据,求出它的样条函数表达式,不过该表达式不是用矩阵直接表示,要求点x`的值,要用函数y`=ppval(pp,x`);
4、pp=csape(x,y,'变界类型','边界值conds');生成各种边界条件的三次样条插值. 其中,(x,y)为数据向量,边界类型可为:
'complete':给定边界一阶导数,即默认的边界条件,Lagrange边界条件
'not-a-knot':非扭结条件,不用给边界值.
'periodic':周期性边界条件,不用给边界值.
'second':给定边界二阶导数.
'variational':自然样条(边界二阶导数为[0,0]。
五、demo
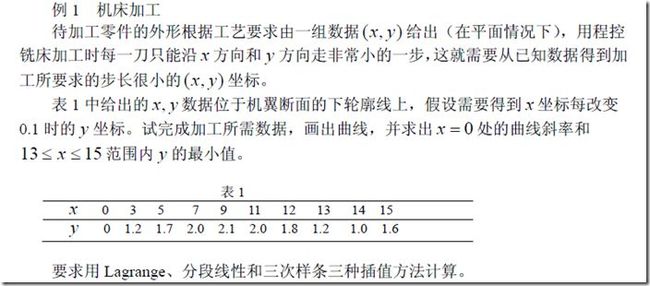
%转载= =
clear,clc x0=[0,3,5,7,9,11,12,13,14,15]; y0=[0,1.2,1.7,2.0,2.1,2.0,1.8,1.2,1.0,1.6]; t=0:0.05:15; %拉格朗日插值函数 y1=lagrange(x0,y0,t);%调用编写的lagrange函数 dy1=(lagrange(x0,y0,0.0001)-lagrange(x0,y0,0))/0.0001%x=0处斜率 min1=min(lagrange(x0,y0,13:0.001:15))%13到15最小值 subplot(2,2,1); plot(x0,y0,'ro',t,y1);%画出曲线 title('拉格朗日插值函数'); %分段线性插值 y2=interp1(x0,y0,t,'spline');%注意区分spline与linear Y2=interp1(x0,y0,t);%默认linear dy2=(interp1(x0,y0,0.0001,'spline')-interp1(x0,y0,0,'spline'))/0.0001%x=0处斜率 min2=min(interp1(x0,y0,13:0.001:15,'spline'))%13到15最小值 subplot(2,2,2); plot(t,y2,'b',t,Y2,'r',x0,y0,'ro');%画出曲线 title('分段线性插值'); legend('边条','线性');%显示图形图例 %三次线条插值A y3=spline(x0,y0,t); dy3=(spline(x0,y0,0.0001)-spline(x0,y0,0))/0.0001%x=0处斜率 min3=min(spline(x0,y0,13:0.001:15))%13到15最小值 subplot(2,2,3); plot(x0,y0,'ro',t,y3);%画出曲线 title('三次线条插值A'); %三次线条插值B pp1=csape(x0,y0);%默认的边界条件,即给定边界一阶导数 pp2=csape(x0,y0,'second');%给定边界二阶导数 y4=ppval(pp1,t); Y4=ppval(pp2,t); dy4=(ppval(pp1,0.0001)-ppval(pp1,0))/0.0001%x=0处斜率 min4=min(ppval(pp1,13:0.001:15))%13到15最小值 subplot(2,2,4); plot(t,y4,'b',t,Y4,'r',x0,y0,'ro');%画出曲线 title('三次线条插值B'); legend('一阶','二阶');
七、二维插值
如果节点是二维的,插值函数是二元函数的话(曲面),我们可以画出三维的效果图
1、插值节点为网络节点
MatLab封装程序
z=interp2(x0,y0,z0,x,y,'method')
a、x0,y0为节点坐标,z0为n*m维矩阵,表示节点的值
b、x0,y0要求一个为行向量一个为列向量
c、z为矩阵,n=length(y),m=length(x) 因为MATLAB是列优先
e、x,y为插值点坐标,z为函数值
然后如果是三次样条插值,可以使用命令
pp=csape({x0,y0},z0,conds,valconds),z=fnval(pp,{x,y})
a、x0,y0为节点坐标,z0为n*m维矩阵,表示节点的值
b、x0,y0要求一个为行向量一个为列向量
c、“conds”与一维相同,一般默认
d、x,y为插值点坐标 ,z为函数值
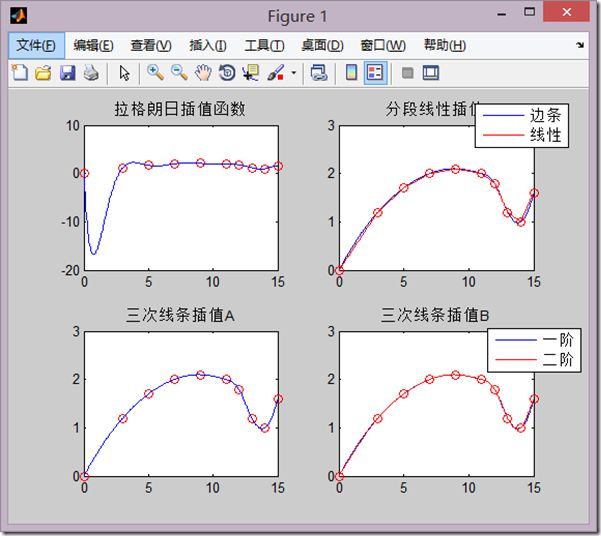
2、demo
clear,clc
%样本点信息
x=100:100:500;
y=100:100:400;
z=[636 697 624 478 450
698 712 630 478 420
680 674 598 412 400
662 626 552 334 310];
%录入样本点信息
pp=csape({x,y},z'); %注意z矩阵的行列所对应的向量
xi=100:10:500;
yi=100:10:400;
cz1=fnval(pp,{xi,yi});
cz2=interp2(x,y,z,xi,yi','spline');
[i,j]=find(cz1==max(max(cz1)))
subplot(1,2,1);
surf(xi,yi,cz1');
shading interp; %插入颜色插值
axis equal;
title('cz1');
subplot(1,2,2);
surf(xi,yi,cz2);
shading interp;
axis equal;
title('cz2');
二、插值节点为散乱节点
1、定义
MATLAB提供了一个函数
zi=griddata(x,y,z,xi,yi)
a、x,y,z为n维向量,就是数据点
b、xi,yi是给定的网格点横纵坐标(插值点),返回zi的值
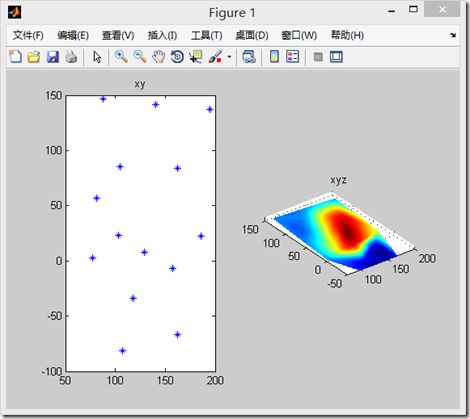
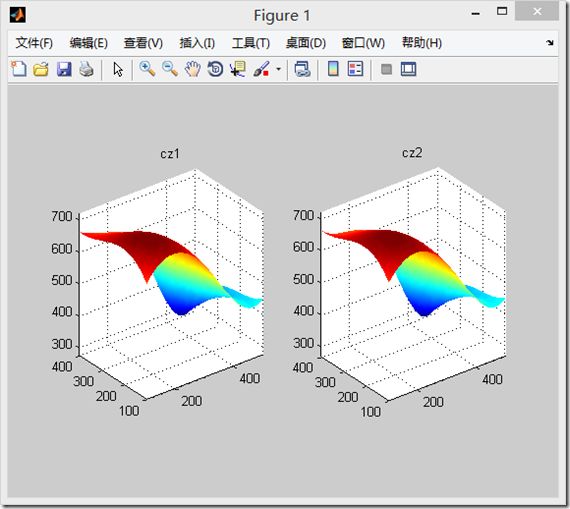
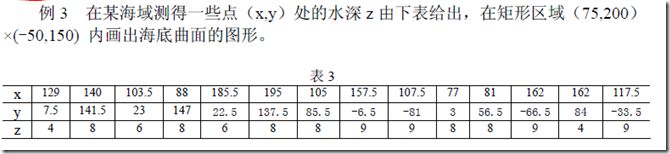
2、demo
clear,clc
%样本点信息
x=[129,140,103.5,88,185.5 195 105 157.5 107.5 77 81 162 162 117.5];
y=[7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.5 84 -33.5];
z=-[4 8 6 8 6 8 8 9 9 8 8 9 4 9];
xi=75:200;
yi=-50:150;
zi=griddata(x,y,z,xi,yi','cubic');
subplot(1,2,1);
plot(x,y,'*');
title('xy');
subplot(1,2,2);
mesh(xi,yi,zi);
shading interp;
axis equal;
title('xyz');