数据结构——队列、最大堆、优先级队列
队列
队列的定义
队列是一种只允许在一端进行插入操作,而在另一端进行删除操作的线性表。队列,顾名思义,就好像我们在超市结账排队一样,先排进队的人先买单,先进入队列里的元素先出队,也就是 先进先出的特点(First In First Out,FIFO),允许插入元素的一端称为队尾,允许删除元素的一端称为队首
队列的操作
初始化队列
检查队空
入队
出队
检查队满
队列的实现
数组实现
我们可以开创一个一维数组用于存放队列的元素,并开创一个head指针和一个tail指针分别指向队首(队列中最后一个元素,即最先入队的元素)和队尾(待插入元素的位置),当删除元素的时候,head向后移动一位;当插入元素的时候,tail向后移动一位,并插入元素;
那么这就会导致一个问题了
在不断地入队出队的操作之后,head和tail都会到达数组的末端,这个时候即使队空,我们也无法再继续添加元素入队了,怎么解决这个问题呢?
当然我们可以开创更多的数组空间,但是这样就造成了前面内存空间的浪费,因此,当head或tail指针指到数组末端的时候,我们应当使其回到数组的起始端,也就相当于将数组空间的头尾相连,组成了一个环形数组
这样前面的问题就解决了,但是在经过几次出队入队的实际操作之后,我们又发现了问题:当我们使用环形数组的时候,队空时:head和tail指向同一位置;队满时:head和tail也指向同一位置。这下我们怎么区分呢?
因此,我们选择浪费数组中一个元素的位置,当tail指向head前面的空位时,称为队满,无法再插入元素;当head和tail指向同一位置时,称为队空
实现代码如下:
void EnQueue(int* nums,int length, int* tail,int key) {
*tail = key;
*tail = (*tail + 1) % length;
}
int DeQueue(int* nums, int length, int* head) {
int ans = nums[*head];
*head = (*head + 1) % length;
return ans;
}
bool IsEmpty(int head, int tail) {
return head == tail;
}
bool IsFull(int head, int tail, int length) {
return (tail+1)%length==head;
}结构体实现
类似于栈的实现,我们也可以通过结构体来实现队列,本质上还是一个链表,只是增多了队首和队尾的指针,并遵循着先进先出的规则
实现代码如下:
typedef struct Queue {//队列结点
int val;
struct Queue* next;
}QueueNode,*LinkNode;
typedef struct Link {//队首队尾指针打包成一个结构体
LinkNode head;
LinkNode tail;
}LinkQueueNode,*LinkQueue;
void EnQueue2(LinkQueue s,int key) {//入队
LinkNode new = (LinkNode)malloc(sizeof(QueueNode));
new->next = NULL;
new->val = 0;//创建空结点给后续tail移位
s->tail->val = key;//key入队
s->tail->next = new;
s->tail = new;//tail向后移一位
}
int DeQueue2(LinkQueue s) {//出队
LinkNode temp = s->head;
int ans = temp->val;
s->head = temp->next;
free(temp);//删除结点释放空间
return ans;
}
bool IsEmpty2(LinkQueue s) {
return s->head == s->tail;//当head和tail重合在空节点时,队列为空
}
LinkQueue Initial() {//初始化队列
LinkQueue s = (LinkQueue)malloc(sizeof(LinkQueueNode));
s->head = s->tail = (LinkNode)malloc(sizeof(QueueNode));
s->tail->val = 0;
s->tail->next = NULL;
return s;
}
int main() {//检验
LinkQueue s = Initial();
for (int i = 0; i < 20; i++) {
EnQueue2(s, i + 1);
}
printf("队列是否为空:%d\n", IsEmpty2(s));
for (int i = 0; i < 20; i++) {
printf("出队:%d\n", DeQueue2(s));
}
printf("队列是否为空:%d\n", IsEmpty2(s));
return 0;
}
最大堆
最大堆是二叉堆的一种情况,因此我们先来了解一下什么是二叉堆
二叉堆
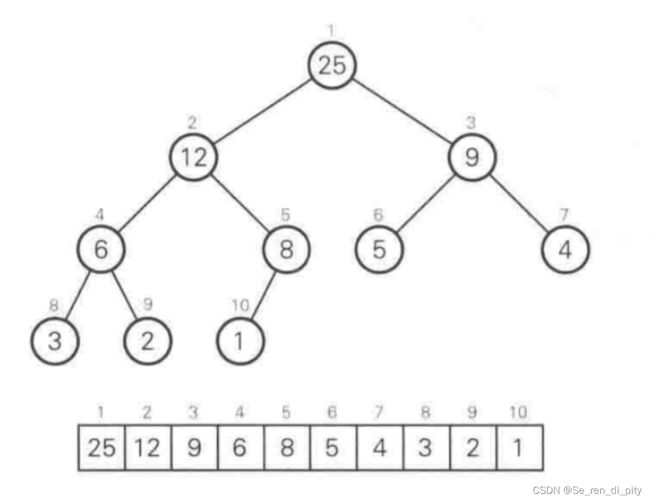
二叉堆是建立在完全二叉树基础之上的数据结构,定义如下:如果一棵完全二叉树各节点的键值与一个数组的各个元素具备下图所示的对应关系,那么这个完全二叉树就是二叉堆
换句话说,二叉堆就是结点具有键值(按一定规则)的完全二叉树,而其结点编号遵循上图所示
二叉堆的逻辑结构虽然是完全二叉树,但实际上是用下标1作为起点的一维数组来表示的。设表示二叉堆的数组为A,二叉堆的大小(元素个数)为n,那么二叉堆的元素就储存在A[1……n]内,其中根的下标为1
由二叉树的数组表示可知,当给定一个结点的下标为i时,i/2为其父结点,2*i与2*i+1分别为其左子结点和右子结点
最大堆与最小堆
二叉堆有且仅有两种:
最大堆:任意结点的键值小于等于其父结点的键值
最小堆:任意结点的键值大于等于其父结点的键值
上图所示就是一个最大堆
应用二叉堆这种数据结构,我们可以在保持数据大小关系的前提下,有效地取出(删除)优先级最高的元素或者添加新元素
最大堆的实现
现给定一个含有若干元素的数组,要求使其元素按照最大堆顺序排列
想要形成最大堆,我们就必须得使父结点的值大于左右子结点的值,那么我们先单独对一个结点展开讨论:
第一步
假设结点的下标为i,则它的左子结点为2*i,右子节点为2*i+1,这里我们假设左右子树已经是最大堆,我们只需要比较这三个结点的值的大小(因为结点i同时也是它的父结点的子结点,所以在这里不需要讨论它的父结点的值,当递归到它的父节点的时候,i自然会作为子结点被讨论),选出其最大值作为父结点,而将两个较小的值交换到子结点,这个时候会出现两种情况:
1.最大值出现在子结点,则将最大值与父结点的值(称之为a)交换(假设与右结点的值交换),这时,交换过去的a不能保证右子树一定是最大堆(因为左子树没有被交换,所以它一定是最大堆),因此,我们需要继续递归到右子结点进行讨论
2.最大值为结点i,则此时不需要交换,结点i为根节点的二叉堆已经是最大堆
第二步
那么还差一个过程来实现我们的第二步,也就是我们一开始的假设:左右子树已经是最大堆
想要创造这个条件并不困难,我们只需要从深度为1的结点开始向上递归第一步的过程,就可以保证左右子树均为最大堆了
而因为最后一个叶结点的下标为n,所以其父结点的下标应该为n/2,这就是深度为1的最右边的结点,我们从该结点开始递归即可
实现代码如下:
//第一步
//nums:给定数组
//n:数组长度
void MaxHeap(int* nums, int n, int i) {
int left= 2 * i;//左子节点
int right = left + 1;//右子节点
int largest = 0;//最大值
if (left <= n && nums[left] > nums[i]) {
largest = left;
}
else {
largest = i;
}
if (right <= n && nums[right] > nums[largest]) {
largest = right;
}//找出最大键值
int temp = nums[i];
nums[i] = nums[largest];
nums[largest] = temp;//交换键值
if (largest != i) {//当发生父子键值交换时
MaxHeap(nums, n, largest);
}
}
//第二步
void BuildMaxHeap(int* nums, int n) {
for (int i = n / 2; i >= 1; i--) {//从下标为n/2的节点开始向上递归
MaxHeap(nums, n, i);
}
}
int main() {
int nums[11] = { 0,4,1,3,2,16,9,10,14,8,7 };
BuildMaxHeap(nums, 10);//注意,二叉堆从下标为1开始
for (int i = 1; i < 11; i++) {
printf("%d\n", nums[i]);
}
return 0;优先级队列
优先级队列是一种数据结构,其储存的数据集合S中,各个元素均包含键值
优先级队列主要进行下述操作:
向集合S中插入元素k
从S中删除键值最大的元素并返回该键值
优先取出最大键值的队列称为最大优先级队列,显然,它可以通过最大堆实现。这里我们用数组A来实现大小为H的二叉堆
更改优先级队列中元素的键值
函数heapIncreaseKey用于增加二叉堆的元素i的键值
假设我们要将A[i]的键值增加为key,为了保证只有在新键值大于等于当前键值时才变更堆,我们要先检查已有键值,然后再更新键值A[i],由于A[i]增加后,其值可能会大于父结点的值,因此需要与其父结点的值进行比较,如果A[i]更大就交换,然后递归调用,即将更新的key值向根的方向移动
向优先级队列中插入元素
我们只需要在数组末端增加一个元素,然后对这个新元素调用heapIncreaseKey,保证其向根的方向移动到合适的位置即可
获取、删除优先级队列中的最大元素
易知队列中的最大值为根节点的键值,因此,我们先将根节点的键值储存在临时变量max中,接着,将二叉堆最末尾的值(数组最后一个元素)移动到根结点的位置,堆的大小H减1。这时,新根节点的左右子树都已经是最大堆,所以只需要对新的根节点调用之前提到的MaxHeap函数,即可恢复最大堆的排列顺序
实现代码如下:
void heapIncreaseKey(int* heap, int i, int key) {//增加键值
if (key < heap[i]) {
return;
}
heap[i] = key;
while (i > 1 && heap[i / 2] < heap[i]) {
int temp = heap[i];
heap[i] = heap[i / 2];
heap[i / 2] = temp;
i /= 2;
}
}
void insertKey(int* heap,int* H, int key) {//插入元素
(*H)++;
heapIncreaseKey(heap, *H, key);
}
int Delete(int* heap,int* H) {//删除并返回最大值
int temp = heap[1];
heap[1] = heap[*H];
(*H)--;
MaxHeap(heap, *H, 1);
return temp;
}
int main() {//检验
int nums[13] = { 0,4,1,3,2,16,9,10,14,8,7,0,0 };
int H = 10;
BuildMaxHeap(nums, 10);
for (int i = 1; i < 11; i++) {
printf("原本:%d\n", nums[i]);
}
heapIncreaseKey(nums, 2, 18);
for (int i = 1; i < 11; i++) {
printf("增加后:%d\n", nums[i]);
}
insertKey(nums, &H, 27);
for (int i = 1; i < 12; i++) {
printf("插入后:%d\n", nums[i]);
}
int ans = Delete(nums, &H);
printf("删除的最大值是:%d\n", ans);
for (int i = 1; i < 11; i++) {
printf("删除后:%d\n", nums[i]);
}
return 0;
}