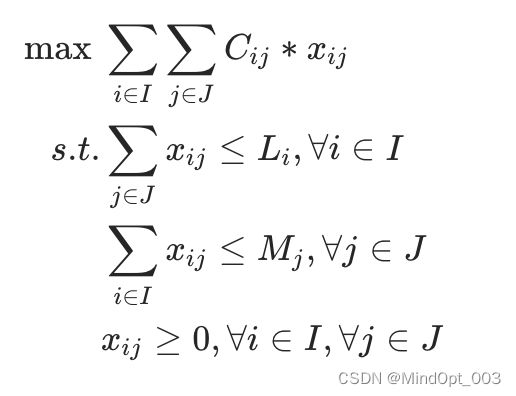MindOpt V1.0优化种植计划问题,新的建模方法
在我们的实际生活中很多问题都可以通过数学规划的方法进行建模,实验求解器工具进行求解,比如工业上的排产排程,如何排产效率更高、金融中的投资理财,怎样投资风险更低等等,本篇将介绍一个农业的场景问题——种植计划。
种植计划是指农业生产中针对不同农作物的种植时间、面积和种植方式等方面的规划安排。根据具体情况进行合理的规划和安排,以实现农作物的高产、优质和可持续发展。
问题描述
一个农民承包了6块耕地,共300亩,准备播种小麦、玉米、蔬菜、瓜果这4种农产品。每个地块由于土质地形不一样,单位面积不同作物的收益是不一样的,且地块的面积不一样,如下表所示。请问要如何安排种植计划,可以得到最大的总收益。
表1:单位面积不同收益(收益 C i j C_{ij} Cij , i ∈ I i \in I i∈I 代表农产品, j ∈ J j \in J j∈J 代表地块, )
| 地块1 | 地块2 | 地块3 | 地块4 | 地块5 | 地块6 | |
|---|---|---|---|---|---|---|
| 小麦 | 500 | 550 | 630 | 1000 | 800 | 700 |
| 玉米 | 800 | 700 | 600 | 950 | 90 | 930 |
| 蔬菜 | 1200 | 1040 | 980 | 860 | 880 | 780 |
| 瓜果 | 1000 | 960 | 840 | 650 | 600 | 700 |
表2:地块面积和计划播种面积限制 ( L i L_i Li代表农产品的播种最大限制, M j M_j Mj代表每个地块的面积最大限制)
| 地块1 | 地块2 | 地块3 | 地块4 | 地块5 | 地块6 | 计划播种面积上限 | |
|---|---|---|---|---|---|---|---|
| 地块面积 | 42 | 56 | 44 | 39 | 60 | 59 | |
| 小麦 | 76 | ||||||
| 玉米 | 88 | ||||||
| 蔬菜 | 40 | ||||||
| 瓜果 | 96 |
然后我们使用线性规划的方法来建模此问题,然后使用求解器工具进行求解。我们可以把线性规划的问题输入求解器的信息转换为:目标、变量、约束。
数学建模
目标:
最大化总收益。
变量:
要安排种植计划,我们这里把每个地块上种不同作物的面积设个未知数,用 x i j x_{ij} xij 代替。
约束:
由于地块面积不同有限制,计划播种面积也有不同,因此根据未知数可以列出不同未知数的加和是有限制的。
这样,变量和约束就如下表所示。
表3 地块面积 x i j x_{ij} xij 和约束
| 地块1 | 地块2 | 地块3 | 地块4 | 地块5 | 地块6 | 播种计划约束 | |
|---|---|---|---|---|---|---|---|
| 小麦 | x 11 x_{11} x11 | x 12 x_{12} x12 | x 13 x_{13} x13 | x 14 x_{14} x14 | x 15 x_{15} x15 | x 16 x_{16} x16 | x 11 + x 12 + . . . + x 16 ≤ 76 x_{11}+x_{12}+...+x_{16}≤76 x11+x12+...+x16≤76 |
| 玉米 | x 21 x_{21} x21 | x 22 x_{22} x22 | x 23 x_{23} x23 | x 24 x_{24} x24 | x 25 x_{25} x25 | x 26 x_{26} x26 | x 21 + x 22 + . . . + x 26 ≤ 88 x_{21}+x_{22}+...+x_{26}≤88 x21+x22+...+x26≤88 |
| 蔬菜 | x 31 x_{31} x31 | x 32 x_{32} x32 | x 33 x_{33} x33 | x 34 x_{34} x34 | x 35 x_{35} x35 | x 36 x_{36} x36 | x 31 + x 32 + . . . + x 36 ≤ 40 x_{31}+x_{32}+...+x_{36}≤40 x31+x32+...+x36≤40 |
| 瓜果 | x 41 x_{41} x41 | x 42 x_{42} x42 | x 43 x_{43} x43 | x 44 x_{44} x44 | x 45 x_{45} x45 | x 46 x_{46} x46 | x 31 + x 32 + . . . + x 36 ≤ 96 x_{31}+x_{32}+...+x_{36}≤96 x31+x32+...+x36≤96 |
| 地块面积约束 | x 11 + x 21 + x 31 + x 41 ≤ 42 x_{11}+x_{21}+x_{31}+x_{41}≤42 x11+x21+x31+x41≤42 | x 12 + x 22 + x 32 + x 42 ≤ 56 x_{12}+x_{22}+x_{32}+x_{42}≤56 x12+x22+x32+x42≤56 | x 13 + x 23 + x 33 + x 43 ≤ 44 x_{13}+x_{23}+x_{33}+x_{43}≤44 x13+x23+x33+x43≤44 | x 14 + x 24 + x 34 + x 44 ≤ 39 x_{14}+x_{24}+x_{34}+x_{44}≤39 x14+x24+x34+x44≤39 | x 15 + x 25 + x 35 + x 45 ≤ 60 x_{15}+x_{25}+x_{35}+x_{45}≤60 x15+x25+x35+x45≤60 | x 16 + x 26 + x 36 + x 46 ≤ 59 x_{16}+x_{26}+x_{36}+x_{46}≤59 x16+x26+x36+x46≤59 |
目标的计算公式:
此时,我们就可以把目标定为:求 f ( x ) f(x) f(x) = sumproduct(收益 C i j C_{ij} Cij*面积 X i j X_{ij} Xij) 的最大值,即每个小作物地块对应收益总和的最大值:
f ( X ) = [ C 11 ∗ x 11 + C 12 ∗ c 12 + . . . + C 16 ∗ x 26 ] + [ C 21 ∗ x 21 + C 22 ∗ x 22 + . . . + C 26 ∗ x 26 ] + . . . + [ C 41 ∗ x 41 + C 42 ∗ x 42 + . . . + C 46 ∗ x 46 ] f(X)=[C_{11}*x_{11}+C_{12}*c_{12}+...+C_{16}*x_{26}]+[C_{21}*x_{21}+C_{22}*x_{22}+...+C_{26}*x_{26}]+...+[C_{41}*x_{41}+C_{42}*x_{42}+...+C_{46}*x_{46}] f(X)=[C11∗x11+C12∗c12+...+C16∗x26]+[C21∗x21+C22∗x22+...+C26∗x26]+...+[C41∗x41+C42∗x42+...+C46∗x46]
= [ 500 ∗ x 11 + 550 ∗ x 12 + . . . + 700 ∗ x 26 ] + [ 800 ∗ x 21 + 700 ∗ x 22 + . . . + 930 ∗ x 26 ] + . . . + [ 1000 ∗ x 41 + 960 ∗ x 42 + . . . + 700 ∗ x 46 ] =[500*x_{11}+550*x_{12}+...+700*x_{26}]+[800*x_{21}+700*x_{22}+...+930*x_{26}]+...+[1000*x_{41}+960*x_{42}+...+700*x_{46}] =[500∗x11+550∗x12+...+700∗x26]+[800∗x21+700∗x22+...+930∗x26]+...+[1000∗x41+960∗x42+...+700∗x46]
即,求解 x i j x_{ij} xij取值等于多少,可得到 f ( x ) f(x) f(x)的值最大。
代码建模求解
直接采用求解器的API,需要查阅API文档来理解API的意思,没有建模语言可读性高。请参阅 https://solver.damo.alibaba.com/doc/html/API2/py/index.html 来查看PythonAPI的使用说明。
本篇使用的是MindOpt V1.0最新版本,与V0.2x的接口不同
此外根据1.0版本使用了一种新的建模方法:List数据,使用numpy。
此种方式利用了numpy,addMVar添加一个 numpy.ndarray 的Mvar。和用addMVar可以矩阵相乘来快速添加多条约束。
此种方法调试的时候容易出错,比如矩阵的方向、维度等。建议可以先小维度数据,生成.lp文件,查看公式是否正确来校验建模的准确性
代码如下:
from mindoptpy import *
import time
import numpy as np
if __name__ == "__main__":
# 声明参数和集合
plant = ["小麦","玉米","蔬菜","瓜果"]
plant_ub = [76,88,40,96]
field = ["地块1","地块2","地块3","地块4","地块5","地块6"]
field_ub = [42, 56, 44, 39, 60, 59]
profit_plant_field =np.array([
[500 ,550 ,630 ,1000 ,800 ,700],
[800 ,700 ,600 ,950 ,90 ,930],
[1200 ,1040 ,980 ,860 ,880 ,780],
[1000 ,960 ,840 ,650 ,600 ,700]
])
alt_plant = [1,1,1,1] # for矩阵相乘得到加和
alt_field = [1,1,1,1,1,1] # for矩阵相乘得到加和
# Step 1. Create a model and change the parameters.
model = Model(name = 'LP_1_plant2')
try:
# Step 2. Input model.
# Change to maximize problem.
model.modelsense = MDO.MAXIMIZE
# Add variables.
#vars = {}
vars = model.addMVar((len(plant),len(field)), obj=profit_plant_field, vtype='C', name="x")
# Add constraints.
#cons = {}
constrs1 = model.addConstr( alt_plant @ vars <= 0)
constrs1.rhs = field_ub
constrs1.lhs = 0
constrs2 = model.addConstr( vars @ alt_field <= 0)
constrs2.rhs = plant_ub
constrs2.lhs = 0
# Step 3. Solve the problem and populate the result.
model.optimize()
time.sleep(1) #for print
model.write("model/plant2.lp") #可以输出文件,观察建模是否正确
model.write("model/plant2.sol")
if model.Status == MDO.OPTIMAL:
print("----\n")
print(f"目标函数是: {model.objval}")
print("决策变量:")
x = vars.X
print(x)
for p in range(len(plant)):
for f in range(len(field)):
if x[p,f] != 0:
print("{0}在{1}的种植面积≈{2:.0f}".format(plant[p],field[f],x[p,f]))
else:
print("无可行解!求解结束状态是:(code {0}).".format(model.Status))
except MindoptError as e:
print("Received Mindopt exception.")
print(" - Code : {}".format(e.code))
print(" - Reason : {}".format(e.message))
except Exception as e:
print("Received other exception.")
print(" - Reason : {}".format(e))
finally:
# Step 4. Free the model.
model.dispose()
本篇可在云上平台查看运行结果,也可对案例复制调试。