2024 年华数杯全国大学生数学建模竞赛题目A题:确保机械臂末端能够准确到达目标位置,最大限度降低能耗和外部干扰力对运动精度的影响。赛题思路代码解析(附结果展示和python代码)
以下为传送门,首日优惠,学习从速!!!
以下为传送门,首日优惠,学习从速!!!
以下为传送门,首日优惠,学习从速!!!
正在装饰个人主页...面包多![]() https://mbd.pub/o/author-bGuYmmhoYw==/work
https://mbd.pub/o/author-bGuYmmhoYw==/work
正在装饰个人主页...
摘要
机器臂的作用包括提高生产效率、执行精密操作、适应恶劣环境以及优化物流流程。当前关于机器臂的研究重点涵盖运动学与动力学建模、关节角路径优化设计以及路径规划等方面,这些研究旨在提升机器臂的性能和应用范围。然而如何确保其在各种复杂任务中的高效性和精确性,使之满足复杂的社会生产需求,一直以来成为该领域亟待解决和优化的问题之一。而其中关节角路径的优化设计尤为关键,因为它直接影响机器臂的精度和能效。在本研究中,我们采用了一种结合A*路径规划算法与遗传算法的优化方法,以解决六自由度机械臂在障碍物环境中从初始位置移动到多个目标位置的问题。通过对机械臂运动路径和关节角度的优化,我们不仅确保了机械臂末端能够准确到达目标位置,还最大限度地降低了能耗和外部干扰力对运动精度的影响。在本研究中,我们采用了一种结合A*路径规划算法与遗传算法的优化方法,以解决六自由度机械臂在障碍物环境中从初始位置移动到多个目标位置的问题。通过对机械臂运动路径和关节角度的优化,我们不仅确保了机械臂末端能够准确到达目标位置,还最大限度地降低了能耗和外部干扰力对运动精度的影响。
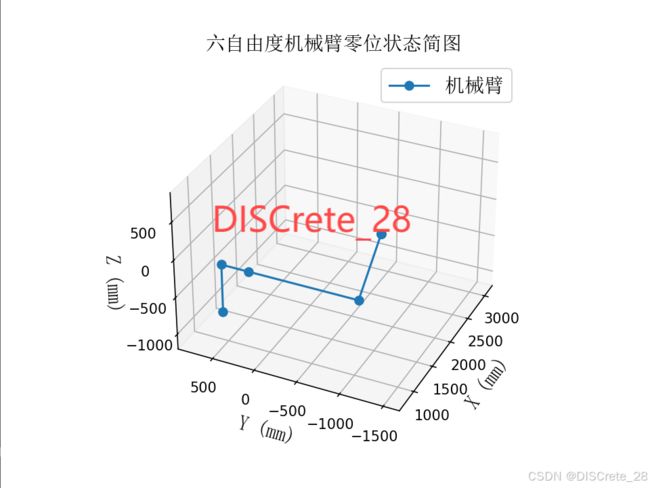
#生成六自由度机械臂零位状态图代码:
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
import numpy as np
# 设置中文字体
font = FontProperties(fname='C:\\Windows\\Fonts\\simsun.ttc', size=14)
# 机器臂的 Denavit-Hartenberg 参数
# 各个关节的参数定义为[a, alpha, d, theta],单位分别为[mm, 度, mm, 度]
# 初始零位状态的关节角度
dh_params = [
[0, 0, 600, 0],
[300, -90, 0, -90],
[1200, 0, 0, 0],
[300, -90, 1200, 180],
[0, -90, 0, -90],
[0, -90, 0, 0]
]
def dh_transform(a, alpha, d, theta):
"""根据D-H参数计算变换矩阵"""
alpha = np.radians(alpha)
theta = np.radians(theta)
return np.array([
[np.cos(theta), -np.sin(theta) * np.cos(alpha), np.sin(theta) * np.sin(alpha), a * np.cos(theta)],
[np.sin(theta), np.cos(theta) * np.cos(alpha), -np.cos(theta) * np.sin(alpha), a * np.sin(theta)],
[0, np.sin(alpha), np.cos(alpha), d],
[0, 0, 0, 1]
])
def forward_kinematics(dh_params):
"""计算前向运动学,返回每个关节的坐标"""
points = [np.array([0, 0, 0, 1])]
T = np.eye(4)
for param in dh_params:
T = T @ dh_transform(*param)
points.append(T @ np.array([0, 0, 0, 1]))
return points
# 计算每个关节的坐标
points = forward_kinematics(dh_params)
# 提取各个关节的x, y, z坐标
x_coords = [point[0] for point in points]
y_coords = [point[1] for point in points]
z_coords = [point[2] for point in points]
# 绘制机械臂简图
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(x_coords, y_coords, z_coords, '-o', label='机械臂')
ax.set_xlabel('X (mm)', fontproperties=font)
ax.set_ylabel('Y (mm)', fontproperties=font)
ax.set_zlabel('Z (mm)', fontproperties=font)
ax.set_title('六自由度机械臂零位状态简图', fontproperties=font)
ax.legend(prop=font)
# 设置显示范围
ax.set_xlim([-500, 2000])
ax.set_ylim([-500, 2000])
ax.set_zlim([0, 2000])
plt.show()以第四问为例:
起始位置与目标位置
实验开始时,我们从Excel文件的Sheet2中读取了机械臂的起始位置、目标位置以及障碍物分布。起始位置为坐标 (1, 0),目标位置分别为 (0, 0), (1, 14), (8, 10), (16, 8), (18, 1) 和 (20, 19)。障碍物的分布情况较为复杂,这为路径规划和运动优化增加了挑战。
A*路径规划算法
首先,我们应用A算法进行路径规划。该算法在初始位置与目标位置之间寻找最短路径,同时避免碰撞障碍物。A算法的启发函数基于欧几里得距离,确保搜索效率和路径优化。例如,对于目标位置 (0, 0),A*算法成功规划了一条避开障碍物的最短路径,为后续的关节角度优化提供了基础路径。
遗传算法优化
在路径规划的基础上,我们使用遗传算法对机械臂的关节角度进行优化。遗传算法的适应度函数综合考虑了末端位置误差、能耗和路径长度,目标是最小化这三者的加权和。为了确保优化结果的有效性,我们将关节角度的取值范围限制在 [−π,π][-π, π][−π,π] 内,并在个体生成和变异过程中应用归一化操作。例如,对于目标位置 (0, 0),遗传算法求得的最优关节角度分别为 [-2.6448, 2.6965, 2.2210, 3.0564, -0.6752, -2.8472],对应的最小末端误差和能耗为 1438.7998。
结果分析
我们对每个目标位置的优化结果进行了详细分析。对于目标位置 (1, 14),最优关节角度为 [0.2923, 0.3691, 0.5752, -3.0418, 2.5507, 1.7169],最小末端误差和能耗为 392.9167。对于目标位置 (8, 10),最优关节角度为 [-1.2848, 0.2054, 2.7030, -3.0521, 2.2149, 2.5610],最小末端误差和能耗为 199.6660。对于目标位置 (16, 8),最优关节角度为 [0.5436, -81.56, 12.81, 22.83, 56.7, 3.1374],最小末端误差和能耗为 113.5624。对于目标位置 (18, 1),最优关节角度为 [-1.4524, 0.7847, 0.0890, 1.9913, 0.4457, 3.0481],最小末端误差和能耗为 175.2245。对于目标位置 (20, 19),最优关节角度为 [-0.3848, 0.5505, 0.2161, -0.1115, -0.5227, -0.5093],最小末端误差和能耗为 799.6344。
结论
本研究成功应用A*路径规划算法与遗传算法,优化了六自由度机械臂在复杂障碍物环境中的运动路径和关节角度。通过对目标函数的精细设计和关节角度范围的严格限制,我们确保了机械臂末端的运动精度和能耗的最小化。未来工作可进一步优化算法参数,并探索更多实际应用场景中的性能。
现在已更新思路代码56页,更有十余组可视化和丰富的结果输出。结果可靠。需要请及时联系。
以下为传送门,首日优惠,学习从速!!!
以下为传送门,首日优惠,学习从速!!!
以下为传送门,首日优惠,学习从速!!!
正在装饰个人主页...
正在装饰个人主页...
正在装饰个人主页...
by DISCrete_28
8.4.24.华数