算法-二分搜索(长期更新)

首先来简介一下二分搜索算法,二分搜索是一种每次砍半的算法,最经典的案例当然是我们的二分查找算法,但是大部分人所认知的二分搜索都是必须要满足这个 数组有序,才可以进行,其实不然,二分的本质逻辑是建立在"砍半",而砍半的本质就是你知道那一半一定没有,而另一半不一定有的前提下,只要满足了这一前提条件,那么你就可以尽可以进行二分…这个算法的时间复杂度是O(logN)
我们这个算法的系列将会长期更新,在遇见好题了之后就会加进来进行整理

情景一 : 二分查找

这个是二分最经典的情景,也就是在一个数组中进行每次砍半的查找元素
代码实现如下

public static int myBinarySearch(int[] nums,int key){
        if(nums == null || nums.length == 0){
            System.out.println("无法进行搜索");
            return -1;
        }
        int left = 0;
        int right = nums.length - 1;
        int mid;
        while(left <= right){
            //请注意这里我们对于我们这个平均值的处理情况
            mid = left + ((right - left)>>1);
            if(nums[mid] > key){
                right = mid - 1;
            }else if(nums[mid] < key){
               left = mid + 1;
            }else{
                return mid;
            }
        }
        return -1;
    }

注意一下我们这里的求其平均值的操作,是利用位运算,其一是防止其溢出,其二是加快运算的速度,因为位运算的速度要远大于除法运算…

情景二 : 找出一个 >= num 的最左侧的位置

这个其实也是二分的逻辑,我们定义一个标记物 ans 初始化置为-1,当我们的mid满足条件的时候,我们就将我们的ans置为 mid ,然后继续二分,当不满足条件的时候,我们就不进行操作,继续二分,然后最后返回我们的 ans 标记物…
代码实现如下 :

/**
     *      情景二 : 找到 >= num 的最左侧的位置
     *      这个基本的逻辑跟二分搜索法其实是一致的,但是也是有一定的差别,比如这个必须要搜索彻底才可以
     *      当每次满足条件的时候,就进行 ans 的更新...直到left == right;
     *
     *      可能你有疑问:为什么我们不进行 <= num 的最左侧位置的查找 ...
     *      因为这个问题是没有意义的..因为只需要判断 nums[0] 跟 key的关系
     * @param nums : 待搜索的数组
     * @param key : 待定的查找元素
     * @return
     */
    public static int findNumMaxLeft(int[] nums,int key){
        if(nums == null || nums.length == 0){
            System.out.println("无法进行搜索");
            return -1;
        }
        int left = 0;
        int right = nums.length - 1;
        int mid;
        int ans = -1;
        while(left <= right){
            mid = left +((right - left) >> 1);
            if(nums[mid] >= key){
                ans = mid;
                right = mid - 1;
            }else if(nums[mid] < key){
                left = mid + 1;
            }
        }
        return ans;
    }

情景三 : 找出一个 <= num 的最右侧的位置

这个其实跟情景二是对称的,原理是一致的,当满足条件的时候记录下来继续进行二分,当不满足条件的时候不进行记录然后继续进行二分,到二分到不能再次进行二分的情况之后,就返回我们的标记ans值…
代码实现如下:

public static int findNumMinRight(int[] nums,int key){
        if(nums == null || nums.length == 0){
            System.out.println("无法进行搜索");
            return -1;
        }
        int left = 0;
        int right = nums.length - 1;
        int mid;
        int ans = -1;
        while(left <= right){
            mid = left +((right - left) >> 1);
            if(nums[mid] <= key){
                left = mid + 1;
                ans = mid;
            }else if(nums[mid] > key){
                right = mid - 1;
            }
        }
        return ans;
    }

leetcode 162 :寻找峰值

首先我们来分析一下这个题干,这个数组中相邻的两个元素都是不相等的,然后让你返回其中的一个峰值(任意一个就可以),那这道题为什么可以进行二分呢…,我们来看体重的假设提示,我们假设 nums[-1] 和 nums[n] 都是 负无穷
首先我们判断一下特殊的情况,假设我们的 第一个元素大于第二个元素,所以此时第一个元素就是局部的峰值(其实这里有点类似函数极值点的概念),对应的如果最后一个元素要大于倒数第二个元素,那么最后一个元素就是峰值

特殊情况的制约
		if(nums == null || nums.length == 0){
		    System.out.println("这个数组不可能存在峰值");
		    return -1;
		}

        //下面都是一些特殊情况的判断...(端点处的极值问题)
        if(nums.length == 1){
            return 0;
        }
        if(nums[0] > nums[1]){
            return 0;
        }
        if(nums[nums.length-1] > nums[nums.length - 2]){
            return nums.length - 1;
        }

下面我们进行一般情况的分析

我们现在不满足特殊条件,所以我们数组的走向是这样的,那么因为我的开头处是上升,终点位置是下降,所以中间的某个位置一定存在至少一个极值点(有点类似中值定理) 所以我们可以进行二分
判断nums[mid] 和 nums[mid-1] 与nums[mid+1] 之间的关系…
而中值位置情况的只有以下四种

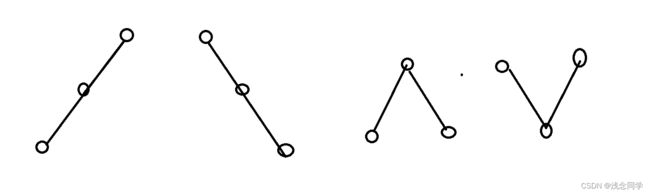
其中 1 2 4 都不是我们所需要的,所以要继续进行二分搜索
所以我们可以写出如下的代码

int left = 1;
        int right = nums.length - 2;
        int mid;
        /**
         * 注意:
         * 这里的控制条件其实非常合理,在中点处一共只有四种情况,而这个循环的控制体系可以控制其中的三种无峰值的情况...
         */
        while(left <= right){
            mid = left +((right - left) >> 1);
            if(nums[mid] < nums[mid - 1]){
                right = mid - 1;
            }else if(nums[mid] < nums [mid + 1]){
                left = mid + 1;
            }else{
                return mid;
            }
        }
        return -1;

下面是我们的完整代码

public static int findPeakNumber(int[] nums){
        if(nums == null || nums.length == 0){
            System.out.println("这个数组不可能存在峰值");
            return -1;
        }

        //下面都是一些特殊情况的判断...(端点处的极值问题)
        if(nums.length == 1){
            return 0;
        }
        if(nums[0] > nums[1]){
            return 0;
        }
        if(nums[nums.length-1] > nums[nums.length - 2]){
            return nums.length - 1;
        }

        //下面是普通的一个情况
        //其实有点类似数学的拉格朗日中值定理
        int left = 1;
        int right = nums.length - 2;
        int mid;
        /**
         * 注意:
         * 这里的控制条件其实非常合理,在中点处一共只有四种情况,而这个循环的控制体系可以控制其中的三种无峰值的情况...
         */
        while(left <= right){
            mid = left +((right - left) >> 1);
            if(nums[mid] < nums[mid - 1]){
                right = mid - 1;
            }else if(nums[mid] < nums [mid + 1]){
                left = mid + 1;
            }else{
                return mid;
            }
        }
        return -1;
    }

leetcode 69 : x 的平方根

这就是一个典型的可以进行二分的题
这个题的核心逻辑跟我们第三个题 : 找出 >= num 的最右侧位置是一致的
值得一提的是,我们这个题要控制我们的算数范围,否则就会出现溢出的问题,下面就是我们的代码解析…没啥可说的了

/**
     *  找出一个数的算术平方根向下取证的那个数然后返回
     * @param x : 待定的开方数
     * @return
     */public static int mySqrt(int x){
        if(x == 0){
            return 0;
        }

        int left = 1;
        int right = x / 2;
        int mid;
        int ans = -1;
        while(left <= right){
            mid = left + ((right - left)>>1);
            if(mid <= x/mid){
                ans = mid;
                left = mid + 1;
            }else if(mid > x/mid){
                right = mid - 1;
            }
        }
        return ans;
    }

唯一要注意的一点就是,这里我们不可以用mid*mid <= x,要改成除法,用mid <= x / mid,否则这个题就会数值溢出导致出错…