HAN!!!!

1. 基本概念

1.1 异构图

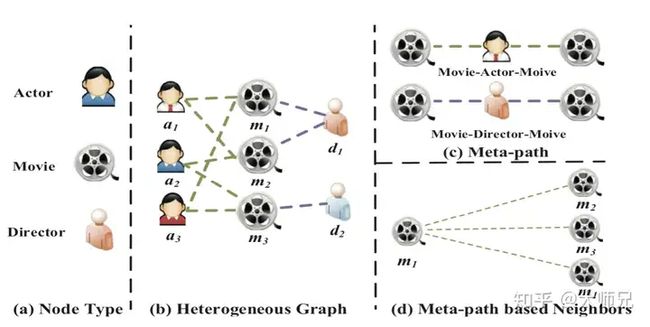
异构图是指不止有一种类型的节点或者边，因此允许不同类型的边或者节点拥有不同维度的特征或者属性。例如作者在论文中列举的IMDB数据（图1），节点的类型包含演员，电影和导演，假如两部电影均由同一个演员参演完成，则可以建立一条电影-演员-电影（MAM）的meta-path或者由同一个导演执导完成，则meta-path的类型为电影-导演-电影（MDM）。

source ~/.bashrc # 如果你使用 bash source ~/.zshrc # 如果你使用 zsh

图1：异构图中的多种节点类型以及多种metapath类型

论文中给出异构图的定义为 G=(V,E) 由节点的集合 V 和节点之间的边 E 组成。异构图也与节点类型的映射函数 ϕ:V→A 以及连接类型的映射函数 ψ:E→R 相关联。 A 和 R 是预先定义好的节点的类型和连接的类型，其中 |A|+|R|≥2 。

1.2 Meta-Path

Meta-Path Φ 的格式为 A1→R1A2→R2⋯→RlAl+1 (缩写为 A1A2⋯Al+1 )，它描述了节点 A1 和 Al+1 之间的一个组合关系 R=R1∘R2∘⋯∘Rl ， ∘ 代表了节点之间的组合操作。例如在图1.c中，两个电影之间可以有MAM和MDM两种关联方式。

1.3 基于meta-path的邻居

给定异构图中的一个节点 i 和一个meta-path Φ ，基于meta-path的邻居 NiΦ 定义为通过类别为 Φ 与节点 i 相连的节点，这里节点的邻居包含它自己。例如图1.d中， m1 有三个基于MAM的metapath的邻居。

上面介绍了异构图中非常重要的三个概念，下面我们详细介绍论文中提出的HAN算法。

2. 算法详解

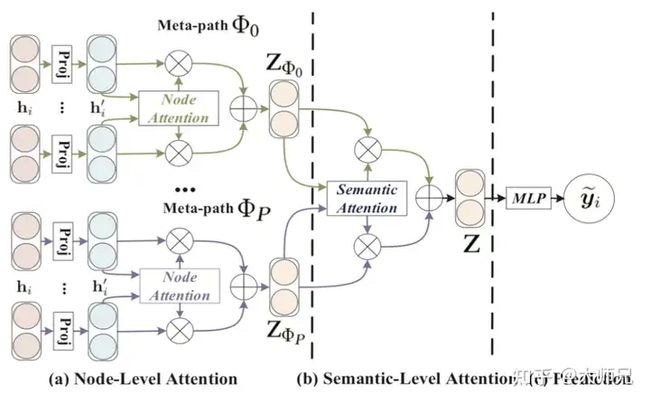
HAN是一个两层的attention架构，分别是节点级别的attention→语义级别的attention，图2便是这个算法的详细结构。首先固定metapath的类别 Φi ，通过节点级别的attention将中心节点的基于 Φi 的邻居节点进行聚合，得到每个metapath的特征向量 ZΦi ，然后再通过语义级别的attention将特征向量 ZΦ 进行聚合，得到最终的特征向量 Z 。最后通过一个MLP得到这个节点的预测值 y~i 。

图2：HAN中的总体框架。(a)是节点级别的attention，聚合后得到每个类型节点的嵌入向量；(b)是语义级别的attention，聚合后得到中心节点的嵌入向量；(c)通过MLP得到预测结果。

2.1 节点级别Attention

在具体的任务中，一个节点在同一个metapath的邻居上有不同的重要性，而同一个中心节点的邻居可能有多种类别，每个类别的节点 ϕi 都有不同维度的特征向量，因此我们的第一步便是通过转换矩阵 Mi 将它们映射到相同的维度。设转换之前的特征向量为 hi ，转换之后的特征向量为 hi′ ，它们之间的计算方式为：

(1)hi′=Mϕi⋅hi.

有了维度相同的特征向量，下一步便是计算每个节点的权值，HAN使用的是self-attention来学习这个权值。对于一个给定的节点对 (i,j) ，它们之间通过metapath Φ 连接，它们之间的节点注意力值 eijΦ 表示节点 j 对节点 i 的重要性，计算方式为：

(2)eijΦ=attnode(hi′,hj′;Φ)=σ(aΦT⋅[hi′||hj′]).

其中 attnode 表示节点级别的attention，对于同一个metapath Φ ，不同基于这个metapath的邻居节点的权值是共享的。 σ 是sigmoid激活函数， ‖ 是拼接操作， aΦ 是节点级别的attention向量。然后通过softmax操作得到每个特征向量的权值系数：

(3)αijΦ=softmax(eijΦ)=exp⁡(σ(aΦT⋅[hi′||hj′]))∑k∈NiΦexp⁡(σ(aΦT⋅[hi′||hk′]))

最后，节点 i 最终的embedding的计算方式为：

(4)ziΦ=σ(∑j∈NiΦαijΦ⋅hj′)

在很多场景中，节点的类别有可能会非常多，这无疑增加了self-attention学习的困难程度，为了解决这个问题，HAN中使用了multi-head attention机制，其中头的个数设置为了8。

(5)ziΦ=‖k=1Kσ(∑j∈NiΦαijΦ⋅hj′)

对于给定的metapath集合 {Φ1,Φ2,⋯,ΦP} ，经过这个节点级别的attention之后，得到 P 组语义相关的embedding，表示为 {Zϕ1,Zϕ2,⋯,ZϕP} 。

2.2 语义级别Attention

异构图除了有多种类别的节点，还有多种类别的边，语义级别的attention便是将不同类型的连接的embedding组合起来，如图2.b所示。假设每个类别的权值为 β ，它的计算方式抽象为：

(6)(β1,β2,⋯,βP)=attsem(Zϕ1,Zϕ2,⋯,ZϕP)

这里 attsem 表示语义级别的attention操作，它的目的是学习每一个边类型的重要性，它首先通过计算语义级别的attention向量 q 和转换之后的每个边类别的embedding得到的，计算方式为：

(7)wΦ=1|V|∑i∈VqT⋅tanh⁡(W⋅ziΦ+b)

其中 q 是语义级别的attention向量， W 是权值矩阵， b 是偏置向量，他们都是需要学习的向量，并且对于所有的metapath都是共享的。通过将softmax作用到根据式(7)得到的 wΦ ，我们便可以得到每个metapath类别的attention权值：

(8)βΦ=exp⁡(wΦi)∑i=1Pexp⁡(wΦi)

最终，根节点的嵌入表示为：

(9)Z=∑i=1PβΦi⋅ZΦi

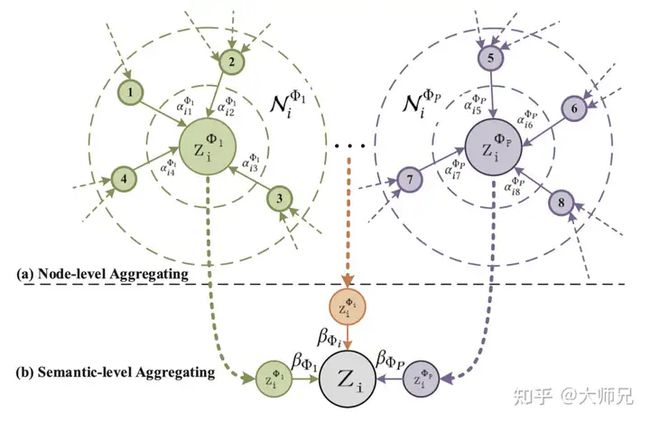
一个更形象的对这两个算法的图示如图3所示：

图3：节点级别的attention和语义级别的attention

2.3 损失函数

HAN是一个半监督模型，我们根据数据集中的有标签数据，使用BP对模型进行训练。使用交叉熵损失函数得到这个算法的损失函数:

(10)L=−∑l∈YLYlln⁡(C⋅Zl)

其中 C 是分类器的参数， YL 是有标签的节点， Yl 和Zl 是有标签数据的标签值和预测值。

3. 总结

这篇文章的算法将attention机制应用到异构图领域中，因为异构图存在节点的多样性和边的多样性，因此作者将attention机制分成了节点级别的attention和语义级别的attention，整体思路非常清晰。

按照作者的思路进一步深入，当学习一个节点的特征时，不同的特征应该扮演着不同的作用，也许给特征层再加一层attention，或者根据图的结构的不同（出入度，邻居类别数等等）赋予不同的权值，也许会有更好的效果。