LCA与RMQ

一、什么是LCA?

      LCA：Least Common Ancestors（最近公共祖先），对于一棵有根树T的任意两个节点u，v，求出LCA(T, u, v)，即离跟最远的节点x，使得x同时是u和v的祖先。

二、算法分类

　　求LCA的算法很多，按照是否在线可以分为在线算法和离线算法。
      在线算法：用比较长的时间做预处理，但是等信息充足以后每次回答询问只需要用比较少的时间。
      离线算法：先把所有的询问读入，然后一起把所有询问回答完成，不是本文所讲，Click here

三、在线算法

　　(1)什么是RMQ?

　　RMQ：给出一个数组A，回答询问RMQ(A, i, j)，即A[i...j]之间的最值的下标。

　　(2)RMQ算法，不是本文所讲，Click here

　　(3)RMQ与LCA 

　　假设一颗有根树，如图所示：

　　

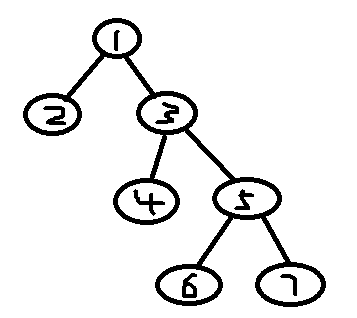
　　我们可以通过深搜（从1节点开始）得到这样一个序列：

　　欧拉序列V：1 2 1 3 4 3 5 6 5 7 5 3 1

　　深度序列D：0 1 0 1 2 1 2 3 2 3 2 1 0

　　First：1 2 4 5 7 8 10

　　First表示节点i在欧拉序列V中第一次出现的位置

　　

　　现在比如我们要求LCA(4，7)

　　那么找到节点4和7第一次出现的位置即：First(4)=5,First(7)=10

　　对应到欧拉序列V中区间[5,10]即：4 3 5 6 5 7

　　发现正好是以3为根的子树，然我我们找到这几个数中深度最小的即D(3)，说明3就是4和7的最近公共祖先

 

　　同理再比如说要求LCA(2,5)，First(2)=2，First(5)=7，找到对应区间[2,7]即2 1 3 4 3 5

　　然后找到深度最小的即1，说明1就是2和5的最近公共祖先。

四：例题

　　HDU 2586

 

　　AC CODE：

　　

#include <iostream>

#include <cstdio>

#include <cstring>

#include <cmath>

using namespace std;

#define min(a,b) ((a)<(b)?(a):(b))

#define N 40010

#define M N*2



struct edge

{

    int u,v,w,next;

}edge[M];

int tot,head[N];



int n,m;

int idx;

bool vis[N];

int ver[2*N];

int dep[2*N];

int first[N];

int dis[N];

int dp[2*N][20];



void init()

{

    tot=0;

    memset(head,-1,sizeof(head));

}

void add(int u,int v,int w)

{

    edge[tot].u=u;

    edge[tot].v=v;

    edge[tot].w=w;

    edge[tot].next=head[u];

    head[u]=tot++;

}

void init2()

{

    idx=0;

    dis[1]=0;

    memset(vis,0,sizeof(vis));

}

void dfs(int u,int d)

{

    vis[u]=1;

    ver[++idx]=u;

    first[u]=idx;

    dep[idx]=d;

    for(int i=head[u];i!=-1;i=edge[i].next){

        int v=edge[i].v;

        if(!vis[v]){

            int w=edge[i].w;

            dis[v]=dis[u]+w;

            dfs(v,d+1);

            ver[++idx]=u;

            dep[idx]=d;

        }

    }

}

void ST(int n)

{

    int i,j;

    for(i=1;i<=n;i++) dp[i][0]=i;

    for(j=1;(1<<j)<=n;j++){

        for(i=1;i<=n;i++){

            if(i+(1<<j)-1<=n){

                int a=dp[i][j-1];

                int b=dp[i+(1<<(j-1))][j-1];

                dp[i][j]=dep[a]<dep[b]?a:b;

            }

        }

    }

}

int RMQ(int i,int j)

{

    int k=(int)(log((double)(j-i+1))/log(2.0));

    int a=dp[i][k],b=dp[j-(1<<k)+1][k];

    return dep[a]<dep[b]?a:b;

}

int LCA(int u,int v)

{

    int x=first[u];

    int y=first[v];

    if(x>y) swap(x,y);

    int res=RMQ(x,y);

    return ver[res];

}

int main()

{

    int T;

    scanf("%d",&T);

    while(T--)

    {

        init();

        scanf("%d%d",&n,&m);

        for(int i=1;i<n;i++)

        {

            int u,v,w;

            scanf("%d%d%d",&u,&v,&w);

            add(u,v,w);

            add(v,u,w);

        }

        init2();

        dfs(1,0);

        ST(2*n-1);

        while(m--)

        {

            int u,v;

            scanf("%d%d",&u,&v);

            int lca=LCA(u,v);

            printf("%d\n",dis[u]+dis[v]-2*dis[lca]);

        }

    }

    return 0;

}